基于C语言下电子常量的反向验证法和模糊统计法的研究

2013-12-24邱王勇庄文波张海涛芦立娟卢晟昊张艳春周桂云

大学物理实验 2013年2期

关键词：统计法油滴C语言

邱王勇，庄文波，张海涛，芦立娟，卢晟昊，张艳春，周桂云

（浙江海洋学院，浙江舟山 316000）

密立根油滴实验的测量方法很多，文章就油滴法得出的实验数据利用C语言进行数据处理，并对反验证法和模糊统计法得出的结果加以比较和研究。

1 实验原理

实验有静态平衡法和动态平衡法两种。

1.1 静态（平衡）测量法

用喷雾器将油滴喷入两块相距为d的平行极板之间。油在喷射撕裂成油滴时，一般都是带电的。设油滴的质量m，所带的电量为q，两极板间的电压为V，如图1所示。如果调节两极板间的电压V，可使两力达到平衡，这时：

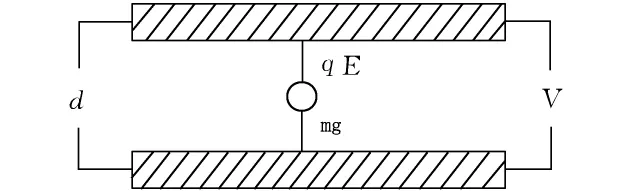
图1 实验演示图

为了测出油滴所带的电量q，除了需测定平衡电压V 和极板间距离d外，还需要测量油滴的质量m。因m很小，需用如下特殊方法测定：平行极板不加电压时，油滴受重力作用而加速下降，由于空气阻力的作用，下降一段距离达到某一速度vg后，阻力fr与重力mg平衡，如图2所示（空气浮力忽略不计），油滴将匀速下降。此时有：

图2 受力分析

其中：η是空气的粘滞系数，是a油滴的半径。经过变换及修正，可得斯托克斯定律：

其中：b为修正常数，b＝6.17×10－6m·c mHg，p为大气压强，单位为厘米汞高。至于油滴匀速下降的速度vg，可用下法测出：当两极板间的电压V为零时，设油滴匀速下降的距离为l，时间为t，则：

最后得到理论公式：

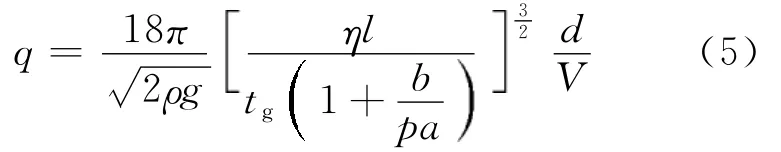
其中：ρ为油的密度，ρ＝ 981 kg m－3；l为油滴匀速下降的距离，l ＝ 2.00×10－3m；g 为重力加速度，g＝9.793 m·s－2；η为空气粘滞系数，η＝1.83×10－5 kg · m－1·s－1；p 为大气压强，p＝76.0 cm（Hg）；b为修正常数，b＝6.17×10－6m·c m（Hg）

1.2 模糊统计法

将数据，q1，q2，…，qi，…，qn，标在数轴上，通过图形，可以直观地看到数据形成疏密有致，一簇一簇的有序分布。如其中间距较大的应该是电荷数的差异，而间距较小的应该是测量随机误差形成的差异对分别属同一簇的数据求平均，可得一组按不同电荷数排列的数据q1，q2qm对这些数据进行多重逐差处理，即e1＝q2－q1，e2＝q3－q2，em－1＝qm－qm－1，只要测量数据足够多，最小差分值ei最可能是电子电量的估计值。

2 实验仪器

HLD－MOD－IX型密立根油滴仪（附喷雾气、油等）。

3 测量原理及数据处理

打开电源，整机预热10分钟；调节仪器水平同时使计时秒表清零；电压200 V左右，打开油雾孔开关，油滴从上极板间小孔落入电场中；调节“平衡电压调节旋钮”驱走不需要的油滴，直到剩下几颗缓慢运动、大小适中的油滴为止，选择其中一颗，仔细调节平衡电压，使油滴静止不动；通过按“提升”按键把油滴提升到显示屏最上端，再按下“测量”键，使油滴开始下降；当油滴转为匀速运动时，可根据需要按下“计／停”键计时；通过按”计／停“键，测量油滴下落为2 mm的距离所经过的时间。停止计时，并立即按“平衡”键或“提升”键，以免油滴逃逸出本电场，此时完成一颗油滴的测量，此时“秒表”上的时间为油滴在2 mm距离匀速运动的时间。如此反复测量多个不同油滴，得到该实验所需要的多组数据。

4 C＋＋程序的使用

下载安装Visual C＋＋6.0程序并运行打开，新建文件选择C／C＋＋Header File，写入程序（见附录1），点击按钮建立Debug文件夹和生成程序。

5 反向验证法的数据处理：

将测得的“V、t1、t2、t3”导入生成的程序，运行结果如图3所示（求得、带电量“q”、电荷数“n”、测量所得单位电荷“ei”以及百分差

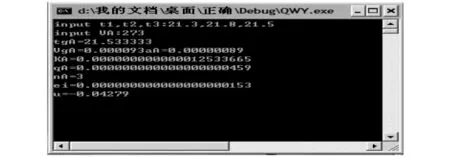
图3 反向验证法C语言程序操作结果

将所得结果填入表1中：

表1 反向验证法数据处理结果记录表

续表1

6 模糊统计法处理：

将C语言程序求得的电荷量q导入Excel表格中利用图表向导工具画散点图，进行模糊统计分析，根据小图，大致可分为7簇，将小图放大后取点，如图4所示。

由图可得各簇电子，并计算相关数据如表2。

图4 电荷q导入Excel表格中散点图

表2 模糊统计法数据处理结果记录

7 实验结果

从表1和表2中看出，反向验证法和模糊统计法得出的百分差分别为4.7%和－2.1%，模糊统计法误差较小。误差产生的原因：将电荷量与已测得的标准电子电荷相比四舍五入取整，会造成很大系统误差；读数时视差的滞后造成的系统误差；

统计法测量时，由于各点之间分界没有理想中那么清晰，故随机误差可能比较大，另划簇时取点的不明确性也会造成较大的系统误差；从表1中百分差最大的几组分析可知，电荷量较小的电荷需要较大电压与较长时间。

本实验运用C语言所设计的程序处理密立根油滴数据，使用方法十分简单，操作直观、简便，而且计算结果一目了然。使用该系统可大大节省数据处理时间，从而提高实验效率与质量，可在实验中应用并推广。

反向验证法与统计法相比较。从验证角度考虑，反向验证法更加准确，误差较小，而系统分析法求得的误差较大，所以在验证目的下，我们应更加提倡反向验证法。但是统计法从总体上分析各组数据大体都在1.60×10－19C附近，误差也不会太大，也有较好的准确性。反向验证法可以较快地处理数据，是现在实验教学中应用较普遍的方法，但其颠倒了因果关系，“密立根油滴实验”本来的物理意义失去了，而统计法是在未知单位电荷情况下求e，符合“密立根油滴实验”的初衷，更能激发学生的实验兴趣。所以从探索角度考虑，我们应该更加提倡使用统计法，因为它更符合逻辑，更加科学。

附录1：

＃include＜stdio.h＞

＃incl ude＜mat h.h＞

main（）

｛

Long float p＝981，g＝9.793，y＝1.83E－5，l＝0.002，P＝76，b＝6.17E－6，d＝0.005，t g A，Vg A，VA，KA，a A，q A，e＝1.60E－19，z，x，v，c，o，ei，m，t，u；

float t1，t2，t3；

int n，n A；

printf（"input t1，t2，t3："）；

scanf（"%f，%f，%f"，＆t1，＆t2，＆t3）；

printf（"input VA："）；

scanf（"%lf"，＆VA）；