“引江济太”调水中望虞河水质变化的规律

张 又，刘 凌，姚秀岚，麻 林，赵 溦

(河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098)

太湖流域具有独特的地形地貌特征，在径流和潮汐双重作用下，人类活动的强烈影响使之易形成重污染区。太湖流域水系与长江、钱塘江相连，水利工程众多，水体流动性差，流域内河网水质普遍超标，水污染问题突出，湖泊富营养化严重［1-2］，迫切需求改善太湖流域水系的连通性，以保障太湖流域的生态环境，实现太流流域水资源的可持续利用［3］。

望虞河位于太湖流域阳澄淀泖区和武澄锡虞区的交界处，连接长江与太湖，是太湖流域“引江济太”的重要调水通道［4］。本研究旨在通过建立马尔科夫模型来分析2008 年“引江济太”调水对望虞河水质的影响，探索江河湖连通性的改善对望虞河水质影响的规律。

1 调水试验概况

2007 年5 月，太湖蓝藻暴发导致无锡市供水危机，“引江济太”应急调度的实施，对改善无锡太湖水源地水质起到了积极作用。为降低2008 年太湖蓝藻大规模暴发的可能性，保障太湖流域供水安全，“引江济太”调水于2008 年1 月提前启动，以进一步探索冬春季引水对减少太湖蓝藻暴发的作用。

2008 年1 月10 日开启常熟枢纽泵站，实施“引江济太”;1 月22 日望亭水利枢纽开闸引水入湖。由于入湖水质受到影响，3 月22—25 日、3 月28 日至4 月2 日望亭水利枢纽关闸，待水质改善后继续开闸引水。6 月9 日望亭水利枢纽关闸，引水结束。

此次调水试验，望虞河上共设置江边闸下、虞义大桥、张桥、大桥角新桥和望亭闸下5 个监测断面，主要监测指标有DO、CODMn、NH3-N、TP 和TN。

2 马尔科夫模型

马尔科夫模型［5］是研究某一事件的状态及状态之间转移规律的模型，它通过对t0时刻事件不同状态的初始概率及状态之间的转移关系来研究t0+t 时刻状态的变化趋势。马尔科夫模型具有无后效性，即状态转移概率仅与转移出发状态i、转移步数k、转移后状态j 有关，而与转移的初始时刻无关［6］。

马尔科夫模型具有描述事物随机变化的良好特性，已大量应用于环境评价与预测方面。钟政林等［7］将马尔科夫模型应用于河流综合水质预报;马占青等［8］应用灰色马尔科夫模型［9］预测城市污水排放量;何斌等［10］用马尔科夫模型求得水质不同级别之间的转移概率，在此基础上建立水质动态评价模型，评价水质的动态变化情况;冯为等［11］建立动态的马尔科夫水质评价模型，对转移概率赋权并计算绝对进步度，在此基础上引出相对进步度的概念;马惠群等［12］将基于Kendall τ 的指标权重引入马尔科夫模型，并应用于大明湖的水质评价。

笔者将模糊隶属度与马尔科夫模型相结合，应用于江河湖连通条件下调水区水质改善度的计算。通过计算望虞河调水试验中调水区水质改善状况的总进步度，以及5 个断面的水质变化进步度，以分析江河湖连通条件下调水区水体污染指标质量改善的规律。

2.1 水质划分

最常见的水质划分方法为:根据水环境质量标准中的水质类别，将水质指标值划分为3 ～6 个状态。这种方法无需将数据规格化，直接根据原始指标值划分等级状态［7，10-11］。但是，当某一指标的检测值大量集中在同一个水质类别时，本方法达不到判断水质变化趋势的目的。因此，需要重新规定隶属范围更小、更精细的状态划分标准。笔者综合考虑各指标监测值的实际情况，对各指标进行规格化处理，将规格化后的指标值划分为11 个等级(即11 种状态)，状态空间表示为E={1，2，…，11}，见表1。

表1 马尔科夫水质状态划分情况

2.2 指标规格化

不同指标的属性值量纲是不同的，为消除量纲带来的影响，需要对指标值进行规格化。规格化就是将一个属性取值范围投射到一个特定范围之内，以消除因数值大小不一而造成评价结果的偏差［13］。指标的规格化一般选用Zadeh 公式:

越大越优型

越小越优型

式中:rij为第j 个样本的第i 个指标的标准化数值;xij为第j 个样本的第i 个指标的实测值;ximax为第i个指标实测值的最大值;ximin为第i 个指标实测值的最小值。

在评价指标中，各指标实测值变化范围大小不一，传统的Zadeh 公式使所有指标实测值的最大、最小值均规格化为1 与0 或0 与1，夸大了实测值变化范围较小的指标在评价中的相对作用，同时削弱了实测值变化范围较大的指标在评价中的相对作用，使评价结果偏离实情［14］。

本文采用以下改进的Zadeh 公式进行计算:越大越优型

越小越优型

式中:x'imax为第i 个指标的理想最大值;x'imin为第i 个指标的理想最小值。

当指标特征值变化范围较小时，指标最大实测值与最小实测值相差不大，计算所得的指标标准化数值也相差不大，反之亦然，因此能较好地反映指标特征值变化的实际情况。同时，各指标的最大实测值ximax与最小实测值ximin用其理想最大值x'imax和理想最小值x'imin代替，各指标的理想最大值和理想最小值可根据样本的实际情况选定。该方法可以有效避免异常的实测最大值或最小值对评价结果的影响。

根据表1 中划分的质量状态，找到每个指标标准化数值rij隶属的状态bij，从而得到指标隶属矩阵:

2.3 概率转移矩阵的构造

假设对m 个指标进行了n 次监测，在这n 次监测中相邻的两次监测值由i 级转变成j 级的总数为kij(i，j=1，2，…，11)，并且认为第n 次监测值转变为本身，i 级内的原始样本数为Ki，则i 级到j 级的转移概率为

由此得到概率转移矩阵:

2.4 进步度计算

概率转移矩阵P 已经可以大致反映监测期内水质的动态发展情况［11］。为了避免马尔科夫链发生多步转移，以及满足极限状态下才能求得稳定概率分布这一苛刻条件［15］，在一步转移矩阵后，利用进步度来动态评估水质变化情况。

进步度sij有几种不同表示方法，本研究选用以下方法计算进步度sij［11］:

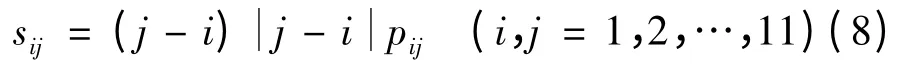
称S=(sij)n×n为概率转移矩阵P 的进步矩阵，则绝对进步度为

将PPD(s)进行规格化，得到相对进步度:

式中，N 即为所分状态的个数，本文中N =11，即Ppd(s)=PPD(s)/100。

相对进步度Ppd(s)是一个范围在［-1，1］之间的数，可以直接反映水质是变好还是变坏。若Ppd(s)＞0，说明污染物指标质量是改善的，反之则是恶化的。水质改善度最大时的相对进步度为1，水质恶化最严重时的相对进步度为-1，相对进步度的绝对值越大说明改善或恶化的程度越大。由相对进步度可以很直观地看出单指标或综合指标的变化情况，而且进步度是一个概率统计参数，可以宏观定量分析水质与水量的关系，不受个别突变值的影响。

3 模型建立

根据太湖流域管理局提供的DO、CODMn、NH3-N、TP 和TN 这5 个指标的检测数据，所有断面监测到的DO 值均可达到Ⅱ类水质及以上，评价时可不予考虑，故选择CODMn(x1)、NH3-N (x2)、TP (x3)和TN (x4)这4 个指标计算水质改善情况的进步度。

根据各指标值的最大、最小值，结合水质等级划分标准［16］，选取各指标的理想最大值和理想最小值，见表2。

表2 各指标理想最大、最小值 mg/L

根据各监测点代表河长(江边闸下7.8 km;虞义大桥13.4 km;张桥15.4 km;大桥角新桥16 km;望亭闸下7.4 km)，将各监测点的CODMn、NH3-N、TP和TN 这4 个指标的值加权平均，可计算得到望虞河全河1—6 月各指标的综合值。

根据式(3)、式(4)对望虞河各指标的综合数值以及各监测点的指标值进行规格化处理，结果见表3 和表4。

表3 望虞河各指标规格化结果

表4 各监测点各指标规格化结果

根据表1 所划分的质量状态，将表3 和表4 中的数据按照式(5)计算，得到隶属矩阵为

根据式(6)～式(8)，运用MATLAB 软件编程，将隶属矩阵直接代入计算得到相对进步度。

经计算得到望虞河调水试验调水区1—6 月的水质变化进步度为:Ppd(s)=0.006 2;江边闸下、虞义大桥、张桥、大桥角新桥及望亭闸下5 个监测断面1—6 月的水质变化进步度分别为:Ppd(s)1=0.057 5;Ppd(s)2= -0.014 2;Ppd(s)3=0.005 7;Ppd(s)4=0.023 6;Ppd(s)5=0.067 6。

4 计算结果分析

编程计算所得的水质变化进步度为水质变化的相对进步度Ppd(s)，其值可以直接反映水质是变好还是变坏。

由计算结果可以看出，望虞河水质在6 个月内总体上是改善的，其进步度为0.006 2，说明其改善程度为0.006 2。通过分析计算结果可知，望虞河水质从1—6 月总的水质变化进步度为0.037 2。从调水上游至下游，各监测断面1—6 月总的水质变化进步度分别为0.345 0、-0.085 2、0.034 2、0.141 6 和0.405 6(图1)，即江边闸下、张桥、大桥角新桥及望亭闸下这4 个监测点的水质改善程度分别为0.345 0、0.034 2、0.141 6 和0.405 6，而虞义大桥监测点的恶化程度为0.085 2。

图1 各监测断面水质变化进步度变化趋势

每个断面的水质变化进步度反映的是相应断面水质随时间的变化情况，即该点水质较之前的变化程度，而不是沿程的变化情况。从图1 可以看出，此次调水期间，望虞河河水在江边闸下断面处的水质改善明显，虞义大桥水质效果最差，从张桥断面以后水质便开始逐渐改善。

从时间跨度上分析水质改善的原因。首先，1—6 月，由冬及夏，水体的自净能力随温度的提升而有所增强，水质因此在一定程度上得到改善;其次，这6 个月中长江水量呈增长趋势，水质随水量增多而有所改善，作为望虞河调水的水源，其水质的改善直接影响望虞河调水通道的第一个监测点，因此江边闸下的水质改善明显;第三，在调水前半程，江水流经望虞河，一定程度上替换了原来的水体，在调水后半程，虽然调水对望虞河河水的替换效果减弱，但污染物沿程的沉积和扩散也成为水质改善的原因之一。由于这些现象多与调水水源和流域汇流的水量有关，故在夏季水量充沛时水质改善效果更为显著。

从沿程汇流的角度分析各监测断面水质改善程度差别的原因。望虞河西岸支流污染较严重，以锡北运河和九里河为甚，其水质超标达4 倍，其他西岸支流也不同程度的水质超标。锡北运河和九里河的汇入，直接影响到虞义大桥和张桥两个监测断面的水质，因此，这两个断面的水质改善情况较差，虞义大桥甚至呈水质恶化的趋势。由于河水自身的净化作用等原因，流动中的水质逐渐好转，至大桥角新桥断面水质已得到明显改善。

5 结 论

a. 运用马尔科夫模型，得到调水后望虞河水质改善情况的进步度，结果显示水质从1 月到6 月总的改善程度为0.037 2。

b. 计算各断面水质变化进步度，得到望虞河水质的变化规律:望虞河江边闸下断面处的水质改善明显，虞义大桥水质呈恶化趋势，从张桥断面以后改善程度逐渐增大。望虞河西岸的重度污染区严重阻碍望虞河水质的改善，以虞义大桥和张桥两个监测点为甚。总体来讲，调水对望虞河水质的改善有明显影响。

c. 采用改进的Zadeh 公式对指标实测值进行规格化，并且根据样本的实际情况选定各指标的理想最大值和理想最小值，可有效避免各实测指标最大值或最小值异常的问题。

d. 调水虽然对望虞河水质有影响，但是调水期间相邻两月的水质指标值变化并不大。本研究采用隶属范围更小、更精细的11 个等级的指标质量状态划分方法，比常规的划分方法更精细，有效避免了因检测值集中在同一水质类别而难以判断水质变化趋势的问题。

e. 在计算水质变化进步度时，采用MATLAB 编程进行计算，效率高，也方便将该方法应用到其他样本的估算中。

［1］任炳相，黄友璋，蒋澄宇. 江苏省太湖污染防治概述［J］. 环境导报，1998(1):23-26. (REN Bingxiang，HUANG Youzhang，JIANG Chengyu. Introduction to the water pollution control of the Taihu Lake in Jiangsu Province［J］. Environment Herald，1998(1):23-26. (in Chinese))

［2］夏立忠，杨林章.太湖流域非点源污染研究与控制［J］.长江流域资源与环境，2003(1):45-49. (XIA Lizhong，YANG Linzhang. Research on non-point source pollution in Tai Lake Region［J］.Resources and Environment in the Yangtze Basin，，2003(1):45-49.(in Chinese))

［3］刘克强，林泽新. 强化太湖流域江河湖连通促进水资源优化配置［J］. 中国水利，2011 (1):33. (LIU Keqiang，LIN Zexin.Strengthening connecting of river and lake in Taihu Region to promote optimal allocation of water resources［J］.China Water Resources，2011(1):33. (in Chinese))

［4］翟淑华，郭孟朴.望虞河引水对太湖影响前景分析［J］.水资源保护，1996 (4):12-15. (ZHAI Suhua，GUO Mengpu. Analysis of prospect of influence of water diversion of Wangyu River to Taihu Lake［J］. Water Resources Protection，1996(4):12-15.(in Chinese))

［5］汪荣鑫. 随进过程［M］. 西安:西安交通大学出版社，1987.

［6］陆传赉. 排队论［M］. 北京:北京邮电学院出版社，1994.

［7］钟政林，曾光明，卓利，等.马尔科夫过程在河流综合水质预报中的应用［J］. 环境工程，1997(2):41-44.(ZHONG Zhenglin，ZENG Guangming，ZHUO Li，et al.Markov process applied to prediction for river comprehensive water quality ［J］. Environmental Engineering，1997(2):41-44.(in Chinese))

［8］马占青，崔广柏，杨宏杰，等.城市污水排放的灰色马尔柯夫预测模型［J］. 河海大学学报:自然科学版，2000，28(5):49-53. (MA Zhanqing，CUI Guangbo，YANG Hongjie，et al. Grey Markonian model for prediction of urban sewage drainage［J］. Journal of Hohai University:Natural Science，2000，28(5):49-53.(in Chinese))

［9］蒋承仪.灰色马尔柯夫预测模型［J］.重庆建筑大学学报，1996(3):117-123. (JIANG Chengyi. Grey Markov forecasting model［J］. Journal of Chongqing Jianzhu University，1996(3):117-123.(in Chinese))

［10］何斌，陈灿，高登好. 水质动态评价的马尔柯夫方法［J］.环境工程，2003，21(3):60-62. (HE Bin，CHEN Can，GAO Denghao. Markov method of dynamic assessment on water quality ［J］. Environmental Engineering，2003，21(3):60-62.(in Chinese))

［11］冯为，邹志红.河流水质的动态马尔柯夫评价［J］.环境工程学报，2007，1 (8):132-135. (FENG Wei，ZOU Zhihong. Dynamic evaluation for water quality of rivers based on Markov process ［J］. Chinese Journal of Environmental Engineering，2007，1 (8):132-135. (in Chinese))

［12］ MA Huiqun，LIU Ling，CHEN Tao. Assessment model based on Markov chain［R］. Piscataway:IEEE Computer Society，2008.

［13］朱明.数据挖掘［M］.合肥:中国科学技术大学出版社，2002.

［14］崔振才，田文苓.模糊数学在水科学应用中的几个问题［J］.河北工程技术高等专科学校学报，2002(2):8-12.(CUI Zhencai，TIAN Wenling.Analysis of some problems in hydroelectric energy with regard to fuzzy set［J］.Journal of Hebei Engineering and Technical College，2002(2):8-12.(in Chinese))

［15］黄宝宏，孙健，魏登云.马尔可夫(Markov)链在体育教学评价中的应用改进［J］.天津体育学院学报，2005，20(2):33-35.(HUANG Baohong，SUN Jian，WEI Dengyun.Improve the application of the Markov chain method on teaching evaluation in physical education［J］. Journal of Tianjin Institute of Physical Education，2005，20(2):33-35.(in Chinese))

［16］GB3838—2002 地表水环境质量标准［S］.