双边四元数傅里叶变换的性质

许旺明

（三峡大学理学院，湖北宜昌 443002）

近年来，国内外学者提出了许多新方法来进行信号处理.值得注意的是四元数傅里叶变换这一工具得到了广泛的研究和应用.在文献［1］中，作者成功地将四元数傅里叶变换运用于二维线性时不变系统.在文献［2－4］中，作者将四元数傅里叶变换运用于彩色图像分析.在文献［5－6］中，与四元数傅里叶变换有关的四元数校正技术得到很大的发展.除此之外，四元数傅里叶变换还被应用于二维解析信号［7］，图像水印［8－9］等.由此可以看出，四元数傅里叶变换已经成为信号处理的有力工具.

由于四元数傅里叶变换具有广泛的应用背景，许多学者对四元数傅里叶变换的性质进行了研究.然而，四元数乘法的非交换性导致四元数傅里叶变换具有3种不同的定义方式，即右边四元数傅里叶变换，双边四元数傅里叶变换，以及左边四元数傅里叶变换.在文献［7］中，Bülow 及其合作者给出了一些双边四元数傅里叶变换的性质并据此引进了二维超复信号.在文献［10］中，Bahri及其合作者研究了右边四元数傅里叶变换，给出了许多右边四元数傅里叶变换的重要性质.作者证明了右边四元数傅里叶变换将实信号分解成具有不同对称性的4个部分.

在本文中，将首先给出文献［7］第5 节的定理1的另一证明，并利用此结果证明双边四元数傅里叶变换也可将二维实信号分解成具有不同对称性的4个部分.

1 双边四元数傅里叶变换的性质

为了更清楚地理解双边四元数傅里叶变换，首先回顾一下四元数的概念.四元数集是一个定义了乘法法则的集合H＝｛a＋ib＋jc＋kd｜a，b，c，d∈R｝，该乘法法则定义如下：

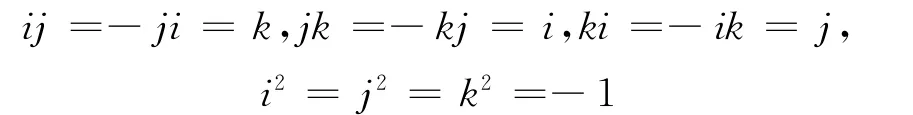
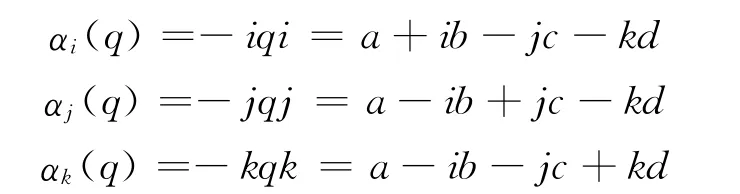
定义函数f∈L2（R2；H）的双边四元数傅里叶变换Fqf 为

其中，x＝（x1，x2），u＝（u1，u2）∈R2.需要指出的是，一般情况下，（1）中的等号是在L2（R2；H）范数意义成立，而不是在点态意义下几乎处处成立，但在本文中，总是假设∫R2｜f（x）｜2d2x 存在，即式（1）中的等号也可视为在点态意义下几乎处处成立.该变换是可逆的，它的逆变换由下面式子给出：

与实函数f 的傅里叶变换具有埃尔米特对称性类似，双边四元数傅里叶变换具有下列性质.

定理1 一个二维实函数f 的双边四元数傅里叶变换Fq具有四元埃尔米特性.

证明：仅仅需要证明（Fqf）（－u1，u2）＝αj（（Fqf）（u1，u2））其余情况类似可得.注意到－jij＝－i并且f 是实的，有：

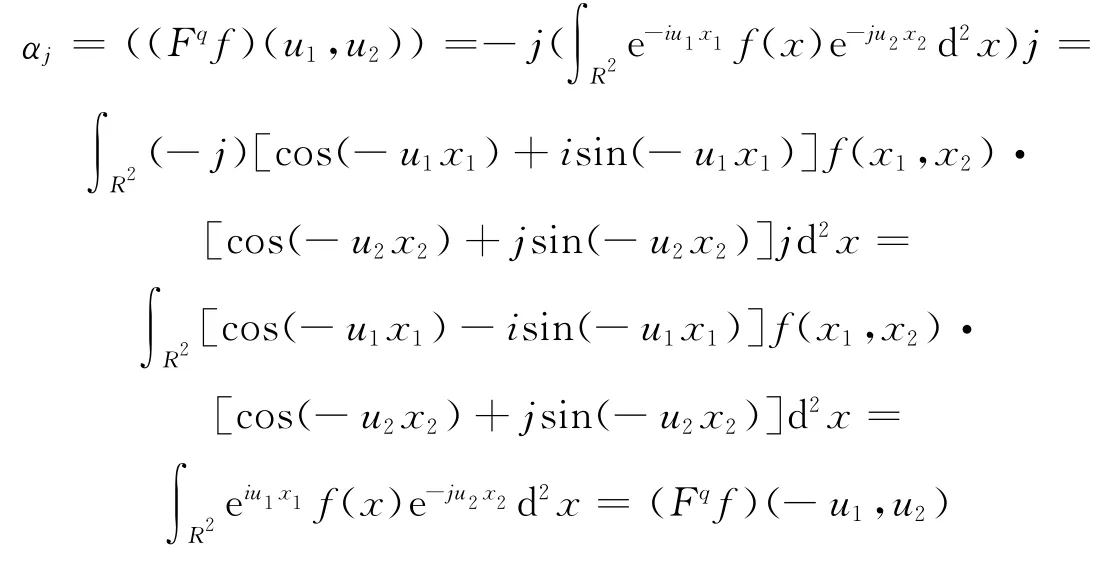
证毕.

一个实函数的傅里叶变换可以分解成具有不同对称性的两个部分：偶对称部分fe→Fe和奇对称部分fo→Fo，其中Fe是实值的，而Fo是纯虚数值的.事实上，能将任意的实函数写成如下形式：

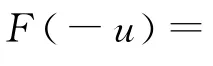
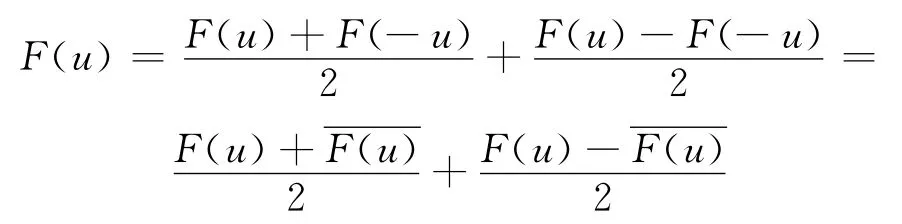
它是一个实值函数与一个纯虚数值函数之和.一个二维实值函数的双边四元数傅里叶变换也具有类似的性质.

定理2 一个二维实值函数f 的双边四元数傅里叶变换Fqf 可以被分解成具有不同对称性的4个部分

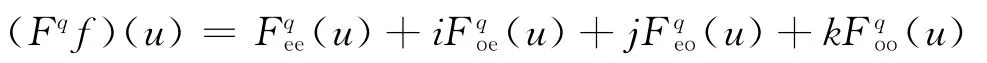
这里下标e和o表示偶和奇对称元素.

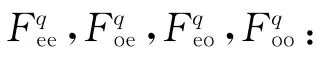
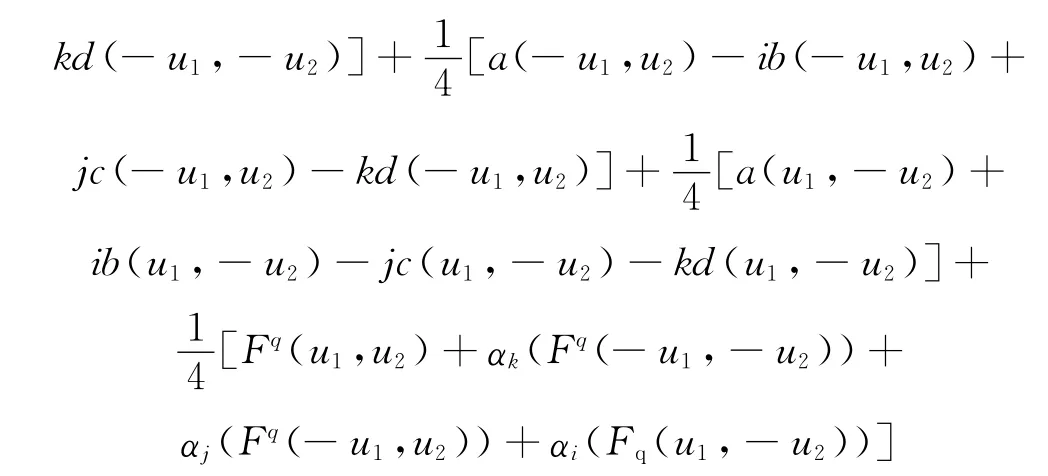
注意到

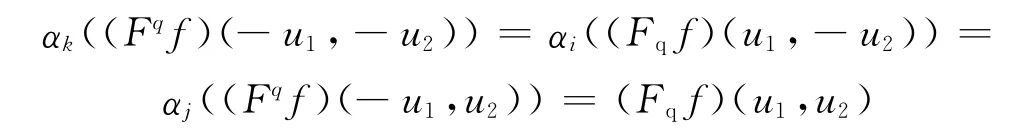
证毕.

3 结 论

为了在图像处理等领域中更好地利用双边四元数傅里叶变换，本文研究了双边四元数傅里叶变换的部分性质.首先重新证明了一个二维实函数的双边四元数傅里叶变换具有四元埃尔米特性.这一重新证明从新的角度理解了双边四元数傅里叶变换.基于这一新的理解，构造性地证明了一个二维实值函数的双边四元数傅里叶变换可以被分解成具有不同对称性的4个部分.

［1］ Ell T A.Quaternion Fourier Transforms for Analysis of 2－dimensional Linear Time－invariant Partial－differential Systems［C］.32nd IEEE Conf.Decision Contr.，San Antonio，TX，Dec.25－17，1993，1830－1841.

［2］ Ell T A，Sangwine S J.Hypercomplex Fourier Trans－forms of Color Images［J］.IEEE Trans.Image Process，2007，16：22－35.

［3］ Sangwine S J.Fourier Transforms of Color Images Using Quaternion or Hypercomplex，Numbers［J］.Electron.Lett，1996，32：1979－1980.

［4］ Sangwine S J，Ell T A.Hypercomplex Fourier Transforms of Color Images［C］.IEEE Int.Conf.Image Process，2001，1：137－140.

［5］ Moxey C，Sangwine S J，Ell T A.Hypercomplex Correlation Techniques for Vector Images［J］.IEEE Trans.Signal Process，2003，51：1941－1953.

［6］ Pei S C，Ding J J，Chang J H.Efficient Implementation of Quaternion Fourier Transform，Convolution，and Correlated by 2－D Complex FFT［J］.IEEE Trans.Signal Process，2001，49：2783－2797.

［7］ Bülow T，Sommer G.Hyper Complex Signals－A Novel Extension of the Analysis to the Multidimensional Case［J］.IEEE Trans.Signal Process，2011，49：2844－2852.

［8］ Bas P，Bihan N L，Chassery J M.Color Image Watermarking Using Quaternion Fourier Transform ［C］.IEEE Int. Conf. Accoustics， Speech and Signal Process.（ICASSP＇03），Hong Kong，2003，3：521－524.

［9］ Chang J H，Pei S C，Ding J J.2D Quaternion Fourier Spectral Analysis and Its Applications［J］.IEEE Int.Symp.Circuits and Systems，2004，3：241－244.

［10］Bahri M，Hitzer E M S，Hayashi A，et al.An Uncertainty Principle for Quaternion Fourier Transform［J］.Computer ＆ Mathematics with Applications，2008，56：2398－2410.