基于分层攻击的社团结构稳定性研究
2013-12-23刘婉璐兰明明
刘婉璐,韩 华,兰明明
(武汉理工大学 理学院,湖北 武汉430070)
社团结构指整个网络是由若干个群或团构成的,每个群内部的节点之间的连接相对非常紧密,而各个群之间的连接相对比较稀疏[1-2]。目前对社团结构的研究主要集中于社团划分算法的探索,而划分出的社团是否稳定,是否会随着网络中节点或边的增减发生变动,是需要进一步探索的问题,即社团结构的稳定性问题。目前,在社团结构稳定性问题的研究中,KARRER 等[3]提出了社团稳定性可以作为社团结构划分优劣的衡量标准。CHENG 等[4]分析了社团结构对于随机攻击的稳定性,对于蓄意攻击的脆弱性。社团结构的稳定性研究有着很重要的现实意义,如在股票网络[5]中,不同的社团代表不同的行业,当股票网络受到打击时,这些行业能否维持稳定对于整个股票网络的特性研究有重要意义,可为投资者决策、行业评估及宏观经济调控等提供现实可循的依据。
目前在复杂网络稳定性研究中,攻击策略主要有蓄意攻击和随机攻击[6]。蓄意攻击包括基于节点的度攻击[7]和基于点介数攻击[8]。随机攻击即随机地攻击网络中的节点或边。对于典型的无标度网络,蓄意攻击是有效的攻击方式,而对于无标度特性不明显的网络,蓄意攻击的优势不但不能完全体现,反而表现了攻击的片面性。而现实世界中存在一些网络,它们不具备典型的无标度特性,如何对这些网络进行有效攻击是需要探讨的问题。笔者提出一种新的攻击策略,称之为分层攻击,即将网络中的节点按某种特性分成n 部分,每一部分取出相应比例的节点,这种攻击策略既避免了随机攻击的盲目性,又避免了蓄意攻击的片面性。
笔者将从攻击策略和社团结构稳定性测度两方面展开研究,先对初始网络进行社团划分,再分别用分层攻击、蓄意攻击和随机攻击对网络进行打击,然后对攻击后的网络进行社团划分,用测度E 衡量攻击前后网络社团划分的差异。通过对分层攻击、蓄意攻击和随机攻击进行对比研究,验证分层攻击策略的有效性。最后用足球俱乐部网和爵士乐队网进行实证研究。
1 复杂网络的攻击策略
在复杂网络稳定性研究中,除了传统的蓄意攻击和随机攻击,吴俊等[9]不仅提出了在不完全信息条件下如何对网络进行攻击的方法,还提出了如何利用信息广度参数和信息精度参数来控制网络的攻击信息。邓宏钟等[10]提出用仿真的方法来研究在不同打击策略下,当复杂网络拓扑结构不同时,其抗毁性能的变化。汪大明[11]提出了社团分离优先攻击策略,他认为社团间的连边较为稀疏,攻击这些“桥梁”应该是一种有效的毁伤策略。
在网络中,对节点的重要性评估主要研究节点的度、点介数、点聚类系数等。节点的度和点介数反映的只是节点本身的特性,而点聚类系数的定义为与该节点相连的k 个节点之间实际存在的边数与总的可能的边数之比。因此,点聚类系数不仅反映了节点本身的特性,也反映了与该点相连的k 个节点所共有的属性,可以将这k 个节点看成一个小社团,故采用节点聚类系数来研究社团结构稳定性更有意义。
1.1 蓄意攻击与随机攻击
设网络中共有N 个节点,对网络进行蓄意攻击时,将节点按其聚类系数从大到小排序,若网络中节点移除比例为f,则依次移除聚类系数较大的Nf 个节点;对网络进行随机攻击时,若网络中节点移除比例为f,则随机移除网络中的Nf 个节点。
1.2 分层攻击
在蓄意攻击和随机攻击的基础上,笔者提出一种新的攻击策略,即分层攻击。分层攻击包括以下步骤:
(1)将点聚类系数从0 到1 分为k 层,分别记为X1,X2,…,Xk。设网络中共有N 个节点,X1,X2,…,Xk中每层包含的节点数为N1,N2,…,Nk,则每层中包含的节点数的比例为α1=N1/N,α2=N2/N,…,αk=Nk/N;
(2)设整个网络需要移除节点的比例为f,则整个网络需要移除的节点数为Nf,故每层需要移除的节点数分别为:M1= α1·Nf = N1/N·Nf =N1f,M2=α2·Nf =N2/N·Nf =N2f,…,Mk=αk·Nf=Nk/N·Nf=Nkf;
(3)在X1,X2,…,Xk中分别移除聚类系数较大的N1f,N2f,…,Nkf 个节点。
对于无标度特性不明显的网络,分层攻击是有效的攻击策略,其综合考虑了各个层次的节点,既避免了随机攻击的盲目性,又避免了蓄意攻击的片面性。因此,从某种意义上来说,分层攻击能够更加全面而又有目的性地攻击网络中的节点,从而达到攻击的目的。
2 社团结构稳定性测度
很多学者对社团结构稳定性测度进行过研究,如KARRER 等提出了用V 测度来衡量社团划分的差异,RAND[12]提出了R 测度,DONGEN[13]研究了D 测度。而PENG 等[14]提出的E 测度与笔者的研究思路较吻合,明确表示出网络受攻击前后其社团划分的差异性,故笔者采用该种测度进行研究。

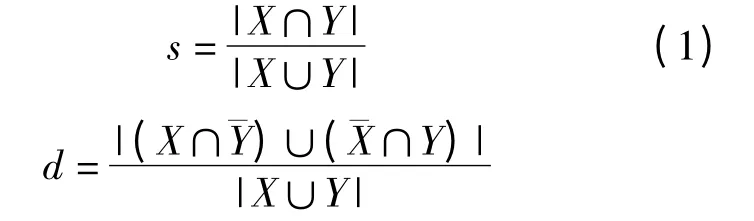
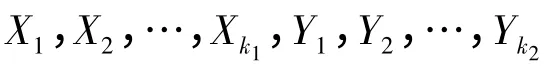

其中,k = max(k1,k2),在该定义下,E 值越小,表明攻击前后社团划分差异性越小,社团结构稳定性越强;E 值越大,表明攻击前后社团划分差异性越大,社团结构表现出脆弱性。
3 仿真实验与分析
足球俱乐部网(football network)和爵士乐队网(jazz band network)有较强的社团性,而通过Matlab 仿真分析得出它们的度分布拟合度不高,故它们不具备明显的无标度特性。因此采用足球俱乐部网和爵士乐队网进行仿真实验,研究其社团结构稳定性问题,并验证对于这种无标度特性不明显的网络,分层攻击是否是有效的攻击策略。
3.1 社团结构划分
足球俱乐部网[15]的数据是由GIRVAN 和NEWMAN 研究2000 年美国大学足球赛所得。联赛一共由115 支足球队组成,这些队伍之间进行了613 场比赛,构建网络时用115 个点代表参赛队伍,若两支队伍之间进行了比赛,则将这两点进行连边。用GN 算法对该网络进行社团结构划分,当划分成9 类时,模块度Q=0.598,达到最大值。
爵士乐队网[16]的数据来自于The Red Hot Jazz Archive,其中198 个节点代表1912—1940 年参加演出的198 个乐队,若两个乐队至少拥有一个相同的音乐家,则将两点进行连边,共有2 742条边。用GN 算法对该网络进行划分,当划分成14 类时,模块度Q=0.403,达到最大值。
3.2 社团结构稳定性
对足球俱乐部网和爵士乐队网,分别用分层攻击,蓄意攻击和随机攻击3 种攻击策略对其进行攻击,再用GN 算法对攻击后的网络进行社团划分,对比研究测度E 随着节点移除比例而发生的变化,如图1 和图2 所示。
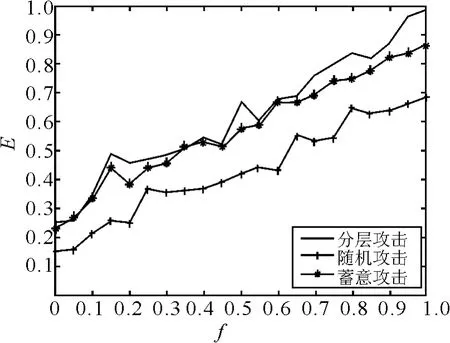
图1 足球俱乐部网测度随节点移除比例的变化
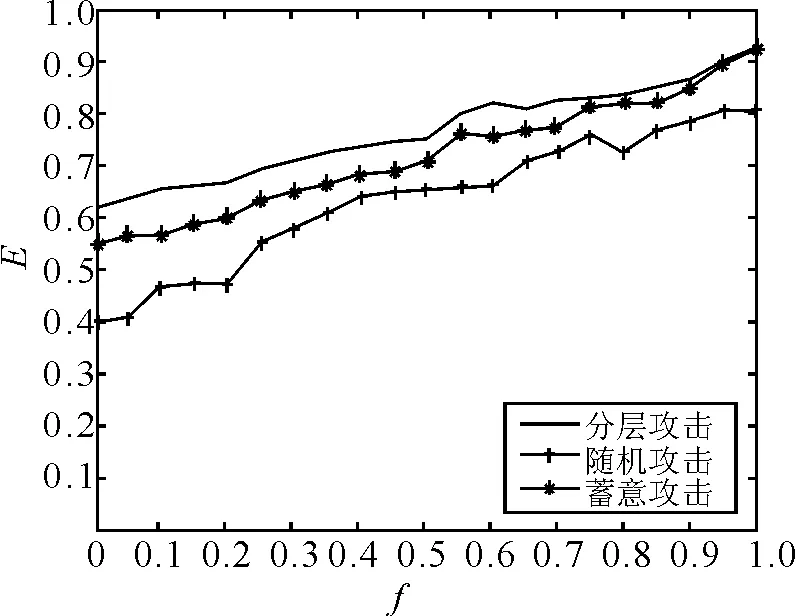
图2 爵士乐队网测度随节点移除比例的变化
由图1 和图2 均可看出,测度E 随节点移除比例整体呈上升趋势,说明随着节点移除比例的增加,社团结构稳定性逐渐降低。测度E 在分层攻击下的值最大,表明用该方法对网络进行攻击,社团划分的差异性最大,社团结构表现出脆弱性。因此,相比于蓄意攻击和随机攻击,分层攻击对这两个网络的攻击效果更好。在蓄意攻击下,测度E 的值也较大,社团结构在蓄意攻击下也表现出脆弱性;但在随机攻击下,测度E 的值相对较小,社团结构在随机攻击下表现出稳定性。而与足球俱乐部网相比,爵士乐队网中测度E 的值偏大,这可能是由于足球网的社团性能更强,因此足球网络攻击前后的社团划分的差异性相对较小。
通过对足球俱乐部网和爵士乐队网的仿真实验,得出了社团结构在分层攻击和蓄意攻击下表现出脆弱性,在随机攻击下表现出稳定性的结论,同时用3 种攻击策略的对比研究验证了对于无标度特性不明显的网络,分层攻击是更加有效的攻击策略。
4 结论
笔者研究了社团结构的稳定性问题,从网络的攻击策略和社团结构稳定性的度量两方面展开研究,在蓄意攻击和随机攻击的基础上提出了分层攻击策略。分别用分层攻击、蓄意攻击和随机攻击对网络进行打击,用测度E 衡量网络攻击前后社团划分的差异,若测度E 的值较大,说明社团结构表现出脆弱性,若测度E 的值较小,说明社团结构表现出稳定性。用足球俱乐部网和爵士乐队网进行仿真实验,结果表明测度E 在分层攻击下的值最大,即在分层攻击下,社团结构更加脆弱,验证了对于无标度特性不明显的网络,分层攻击比蓄意攻击和随机攻击对网络的攻击效果更好。在实际操作中,若要对网络进行破坏,可采取分层攻击策略,提高攻击效果;相应地,若要防止网络被破坏,则要对不同类别的节点加以保护,增强网络的抗毁性能。
[1] 汪小帆,李翔,陈关荣. 复杂网络理论及其应用[M].北京:清华大学出版社,2006:54-87.
[2] 解㑇,汪小帆.复杂网络中的社团结构分析算法研究综述[J].复杂系统与复杂性科学,2005,2(3):1-12.
[3] KARRER B,LEVINA E,NEWMAN M E J.Robustness of community structure in networks[J]. Phys Rev E,2008 (77):46-59.
[4] CHENG J,LI X J,DI Z R,et al. The attack tolerance of community structure in complex networks[EB/OL].[2012-11-23]. http://arxiv. org/abs/1001.2377v1.
[5] 马源源,庄新田,李凌轩.沪深两市股权关联网络的社团结构及其稳健性[J]. 系统工程理论与实践,2011,31(12):2241-2250.
[6] ALBERT R,JEONG H,BARABASI A L.Error and attack tolerance of complex networks[J].Nature,2000,(406):378-382.
[7] 黄金源,张宁,肖仰华.基于拷贝模型的复杂网络鲁棒性研究[J].计算机应用研究,2010,27(4):1403-1406.
[8] BARTHELEMY M . Betweenness centrality in large complex networks[J]. Euro Phys J B,2004,38(2):163-168.
[9] 吴俊,谭跃进,邓宏钟.基于不等概率抽样的不完全信息条件下复杂网络抗毁性模型[J]. 系统工程理论与实践,2010,30(7):1207-1217.
[10]邓宏钟,吴俊,李勇,等. 复杂网络拓扑结构对系统抗毁性影响研究[J]. 系统工程与电子技术,2008,30(12):2425-2428.
[11]汪大明.复杂网络社团模型与结构研究[D].长沙:国防科学技术大学图书馆,2010.
[12] RAND W M. Objective criteria for the evaluation of clustering methods[J].Journal of American Statistical Association,1971(66):846-850.
[13] DONGEN S V. Performance criteria for graph clustering and Markov cluster experiments[M].The Netherlands:Centre for Mathematics and Computer Science Amsterdam,2000:54-98.
[14]PENG Z,LI M H,WU J S,et al.The community structure of scientific collaboration network[J].Physica A,2006(367):577-583.
[15]GIRVAN M,NEWMAN M E J.Community structure in social and biological networks [J]. Proc Natl Aead Sei,2002(99):7821-7826.
[16] GLEISER P,DANON L. Community structure in jazz[J].Adv Complex Syst,2003,6(4):565-573.
