模糊评语集的证据理论在质量评估中的应用

2013-12-23卞树檀

武汉理工大学学报（信息与管理工程版） 2013年3期

刘仁，卞树檀，于强

(第二炮兵工程大学101 教研室，陕西西安710025)

针对评估中存在的不确定性，笔者引入模糊评语集来描述不确定性，利用证据理论在处理不确定问题中的优势，通过多指标证据的合成，降低评估的不确定度，使评估结果尽量准确。评估作为一种由定性到定量，再由定量到定性的过程，过分依赖定量分析，通过繁琐的数值计算得到的精确结果，却不能给出结果的可信度，本身就没有实际意义。因而笔者结合原始测试数据，利用模糊评语集得出的评估结果更切合实际。

1 证据理论

1.1 证据理论基本概念

证据理论又称信任函数理论，它是经典概率论的一种扩充形式。20 世纪60 年代，DEMPSTER 在多值映射的工作中把证据的信任函数与概率的上下值相联系，提供了一个构造不确定性推理模型的一般框架。20 世纪70 年代，SHARE对DEMPSTER 的理论进行了扩充和完善，用信任函数和似真度量重新解释了多值映射，在此基础上形成了处理不确定信息的证据理论［2］。

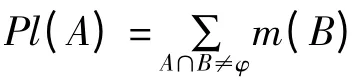
1.2 融合指标权重的基本可信度分布

在DEMPSTER 组合规则中，对各信息源所提供的证据信息是平等对待的，各组证据之间没有优劣的区分。这在很多时候是不合理的，特别是在各信息源的可靠性、重要性和可信度差异很大的情况下，DEMPSTER 组合规则可能会给出与客观情况不相符的结果［3］。在武器装备质量评估中，由于各指标对系统质量影响的重要性程度不一致，存在一些关键指标，因此，在进行证据组合时必须考虑重要性的差异。笔者通过证据基本可信度分配组合前的调整，形成了融合各指标权重信息的基本可信度分配函数。在进行各证据合成时，对于权重高于平均权重的证据支持的命题应该更加支持，反对的命题更加反对;对于权重低于平均权重的证据支持的命题支持度与反对的命题反对度都应该有所减弱。利用式(1)对证据的基本可信度分配和指标权重进行融合:

总体来看，情报信息机构的知识服务在经过几年的理论导入之后，随着研究和实践的深入，以文献为载体的成果数量在一个较长的时间里出现了波动增长的态势。近年来统计数据的下滑，反映了在大数据、云计算和人工智能等现代信息技术迅速发展的条件下，知识服务的理论和实践进入了蛰伏期和升级换挡阶段。

当各指标的权重相等时，显然有m wk=1，其中m 为指标数量，即调整前后证据的基本可信度分配函数保持不变，与主观逻辑一致。由于确定各指标权重的方法很多，且不是笔者的研究重点，在此不再赘述。

1.3 证据理论的缺点

证据理论在处理不确定性信息融合方面虽已有一些应用，但同时也存在一些问题，其中最突出的是证据冲突问题。证据理论在解决低冲突问题时具有较好的效果，但在处理高冲突问题时合成的结果往往会产生悖论，在证据完全冲突时，证据理论甚至无法进行合成。

设有两个证据m1和m2，焦元为A、B、C，基本可信度分配函数为m1(A)=0.9，m1(B)=0.1，m1(C)=0.0，m2(C)=1.0，m2(A)=0.0，m2(B)=0.1，m2(C)=0.9，则利用合成规则合成的结果为:K=0.99，m(A)=0.0，m(B)=1.0，m(C)=0.0。虽然m1、m2对B 的支持度都较低，但融合结果却认为命题B 为真，不符合常理。分析可知，只要某一个证据的某焦元基本可信度分配函数为0，无论其他证据如何支持它，最终的合成结果对该焦元的基本可信度分配函数都为0，这显然是不合理的，达不到融合各证据的目的。

设有两个证据E1和E2，焦元分别为A、B，基本可信度分配函数为m1(A)=1.0，m1(B)=0.0，m2(A)=0.0，m2(B)=1.0。则K =1，无法对其进行合成。

由此可见证据理论在处理实际工作中遇到数据异常问题时显得力不从心，该理论的容错性较差。

2 基于相似系数的证据理论

定义5 Ei和Ej为识别框架Θ 上的两个证据，其基本信任函数分别为mi、mj。证据Ei的焦元为{mi(A1)，mi(A2)，…，mi(An)}，证据Ej的焦元为{mj(B1)，mj(B2)，…，mj(Bm)}，则证据Ei和Ej间的相似系数可表示为:

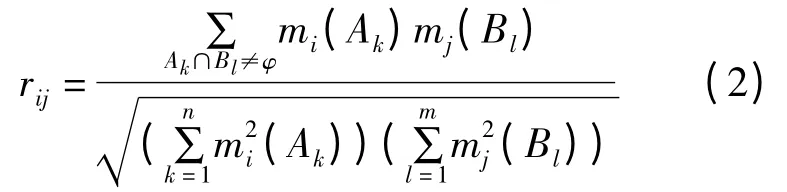
相似系数rij用来度量证据之间的相似程度。由式(2)可知，rij∈［0，1］，其值越大，说明相似性越好。当两个证据完全冲突时，rij=0，当两个证据完全相同时，rij=1，可知相似系数的定义与主观逻辑一致［4］。

假设现有n 个证据，利用式(2)可求得n 个证据相互之间的相似系数矩阵R =(rij)n×n，显然R 是一个对称矩阵，且主对角线上元素为1。

定义6 每一证据与其他证据的相似系数相加的数值作为其他证据对该证据的支持度，即:

将各证据的支持度归一化，作为证据Ei的可信度，其表达式为:

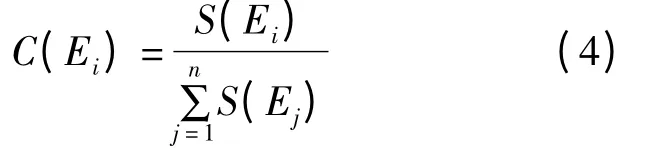
可信度越高表明证据越可靠，利用可信度对各证据的基本可信度分配进行加权平均，作为证据合成的基本可信度分配。若存在n 个证据，则将加权平均的基本可信度分配进行n－1 次合成。

3 模糊评语集

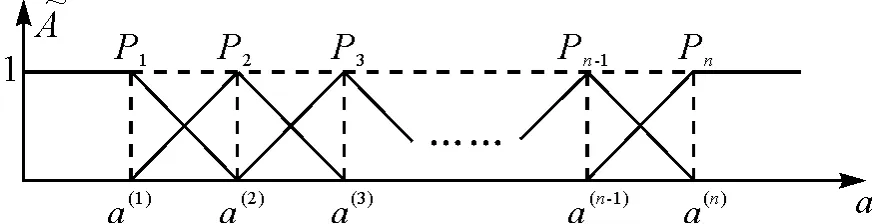
图1 模糊评语集的隶属度

其中:

4 算例

某武器装备的质量由6 个指标参数F ={f1，f2，f3，f4，f5，f6}决定，测试数据预处理后为［0.864，0.831，0.904，0.861，0.877，0.897］。由文献［9］求得各指标权重为W =［0. 068 0，0. 076 8，0.330 2，0.116 6，0.169 4，0.239 1］。

(1)由专家组确定质量的模糊评语集为P ={很好，好，一般，差，很差}，模糊评语集的模糊三角隶属函数如图2 所示。

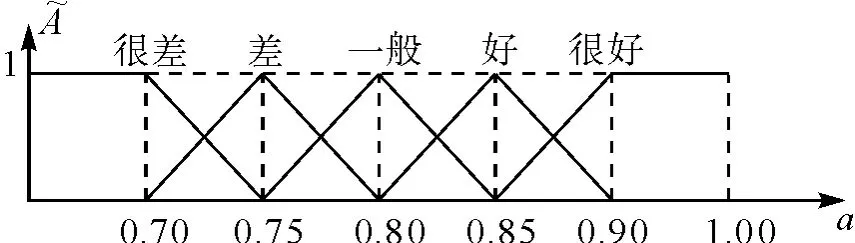
图2 指标的模糊评语集标准

(3)融合指标权重后的基本可信度分配为A11=［0.404 8，0.595 2，0.000 0，0.000 0，0.000 0］，A12=［0.000 0，0.556 2，0.443 8，0.000 0，0.000 0］，A13=［1.000 0，0.000 0，0.000 0，0.000 0，0.000 0］，A14=［0.292 0，0.708 0，0.000 0，0.000 0，0.000 0］，A15=［0.540 7，0.459 3，0.000 0，0.000 0，0.000 0］，A16=［0.981 1，0.018 9，0.000 0，0.000 0，0.000 0］。

(4)由于现有的证据高度冲突，采用基于相似系数的证据理论对证据进行合成。求得各证据间的相似系数矩阵。

求得的各证据可信度分别为［0. 203 2，0.102 9，0.147 4，0.183 6，0.212 2，0.150 7］。以各证据的可信度为权重，对证据的基本可信度分配进行加权平均可得证据的基本可信度分配为［0.545 8，0.408 5，0.045 7，0.000 0，0.000 0］。由于有6 个指标提供了6 个证据，现对加权平均得到的基本可信度分配利用证据理论合成规则进行5次合成，可得装备相对模糊评语集的最终合成结果为［0.850 6，0.149 4，0.000 0，0.000 0，0.000 0］。

(5)利用最大隶属度原则max m(pi)=m(很好)=0.850 6，可得装备的质量水平为很好，且对其质量水平为很好的支持度较高，比较确定。