寄售模式下基于旁支付契约设计的供应链协调

朱 燕，牛占文，何龙飞

(天津大学 管理与经济学部，天津300072)

供应链管理是设计和保持一种良好的契约和模式，通过资源集成，借助合作企业的力量更好地发挥自身的核心优势，使自身和整个供应网络获得竞争优势的一个过程［1］。在现实中，供应链各成员总是以自身利益最大化为目标进行决策。在这种分散决策情形下，供应链成员的利己行为将导致供应链低效，如何设计契约来减小利己行为导致的低效并改善供应链的系统收益一直是供应链管理研究的热点。笔者通过在寄售价格契约中引入旁支付来解决由单个供应商和单个零售商组成的两级供应链的协调问题。

所谓寄售，是指供应商将货物存放在购买商的库存中，在货物没有被购买商使用或销售之前，货物的所有权归供应商所有，购买商只有在使用或销售货物后才向供应商支付费用。在现实生活中，寄售模式非常常见。例如，许多生产商(Dell、Philip、Honeywell、海尔、长虹等)都要求供应商将生产用的零部件、原材料等存放在自己的仓库里，用完后再与供应商结账;很多宾馆房间里存放的各种饮料、食品和闭路节目点播等实际上也是一种寄售模式;甚至连电子商务网站(如eBay、Amazon.com、阿里巴巴、淘宝、易趣等)所采用的也是一种寄售合同［2］。

典型的寄售契约有两种形式:①供应商将货物存放在零售商处，首先由零售商决定从每单位产品的销售收入中提取收入分配比例，然后再由供应商决定寄售产品的销售价格和寄售数量，称为基于收益共享的寄售契约;②首先由供应商决定寄售产品的批发价格和寄售数量，然后由零售商决定寄售产品的零售价格和订货量或零售价格，称为寄售价格契约。

RUBIN 等［3］将旁支付定义为“存在于供应商和零售商之间的用于激励双方脱离各自的最优决策的额外货币性支付”。

关注于分散决策并通过旁支付契约设计来协调供应链的文献已经有很多，如文献［4－10］，但研究寄售模式下的供应链协调问题的文献则相对较少。WANG［11－12］等基于收益共享寄售契约下供应链的收益情况，比较了集中决策和分散决策下的供应链收益，但没有研究供应链协调问题。ZHANG 等［13－14］在WANG 等基础上，进一步研究了供应链协调问题，ZHANG 等运用基于收益共享的旁支付契约实现供应链协调，但ZHANG 等认为实现协调后的系统收益增量可以在零售商与供应商之间任意分配，并没有考虑收益增量分配的合理性和公平性问题。

RU 等［15］研究了在批发价格契约的寄售模式下，供应商和零售商谁来决定寄售库存量的问题。分别在VMCI 和RMCI 寄售价格契约的条件下，将分散决策的收益与集中决策进行比较，但没有进一步研究如何实现供应链协调的问题。

笔者在RU 和WANG 研究的VMCI 寄售价格契约基础上，引入了旁支付来减少分散决策下的供应链收益损失。重点研究了如何设计契约参数以保证供应链系统收益增量分配的合理性和公平性的问题，运用Rubinstein 讨价还价模型求解供应链双方的收益增量的分配比。

1 基本问题描述和集中决策模型

1.1 基本问题描述

(1)问题描述和模型假设。笔者以单供应商和单零售商组成的两级供应链为研究对象，假设该供应链由供应商主导(供应商具有优先决策权)。供应商通过寄售的方式销售产品，零售商只有在将产品销售出去之后才向供应商付款，供应商承担库存持有成本。供应商与零售商之间采用的是基于批发价格的寄售契约，且由供应商决定寄售在零售商处的产品数量。

模型假设如下:①只考虑一个销售周期，在每个销售周期开始之前，供应商生产q 单位的某种产品并通过零售商进行销售，假设供应商只生产一种产品;②供应商生产单位产品的生产变动成本和库存持有成本为cM，零售商销售每单位产品发生的相关成本为cR，c =cM+cR为销售每单位产品供应链发生的总成本，α =cR/c 为零售商的单位成本占供应链的单位成本的比例，那么1－α为供应商的单位成本占供应链的单位成本的比例;③为了简化模型，假设期末没有销售出去的产品不存在残值和任何处置成本，同时，不考虑缺货成本。

(2)需求函数。假设在单销售周期里，市场对供应商产品的需求随机且与产品的价格相关，采用乘法模型来反映需求的随机性。供应商产品的市场需求用D(p)来表示:

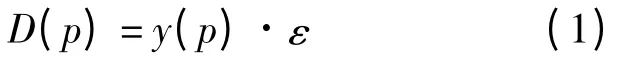
式中:p 为供应商产品销售价格;y(p)为供应商产品市场需求与价格之间的确定性关系;ε 为需求的随机性，令ε∈［A，B］，B ＞A≥0 ，E(ε)=μ。

根据文献［11］，y(p)采用如下形式:

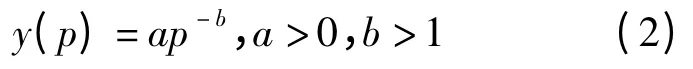
式中，b 为产品的需求价格弹性，表示需求对供应商自身产品价格变动的反应灵敏程度。需求价格弹性可以大于1、小于1 或等于1，分别表示需求富有弹性、需求缺乏弹性和需求单一弹性。需求价格弹性越大，表示需求对价格变化越敏感。笔者假设供应商的产品是需求富有弹性的，因此有b ＞1。

(3)符号说明。系统参数和决策变量符号如表1 所示。

表1 各系统参数和决策变量符号

1.2 集中决策

假设在集中决策情形下，由一个集中决策者代替供应商和零售商做决策，其目标是确定最优的(p*，q*)以最大化供应链总收益ΠC(p，q)，即:

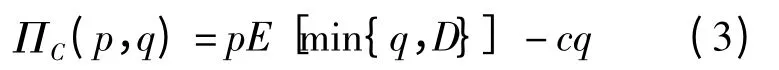
根据文献［16－17］定义z=q/y(p)，z 为供应链的产品数量对市场期望需求的满足率，反映产品的平均可获得性。那么选择最优决策(p*，q*)等价于选择最优的(p*，z*)。将q =y(p)代入式(3)，可得供应链的总期望收益为:

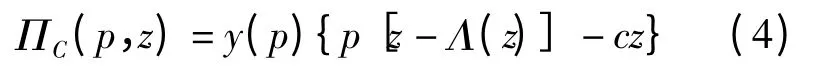
由一阶条件∂ΠC(p，z)/∂p=0，可得产品的最优销售价格为:

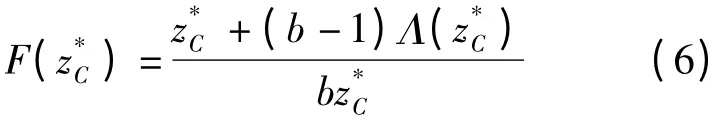
由式(5)和式(6)可得产品最优销售价格为:

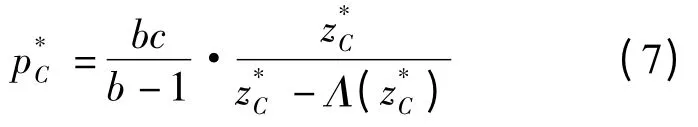
将式(6)和式(7)代入式(4)，可得供应链的总期望收益为:

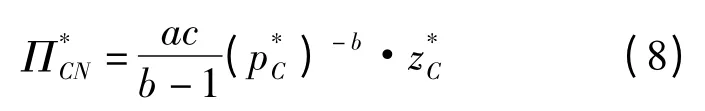
集中决策模型的结果将作为分散决策的比较基准。

2 分散决策

在分散决策情形下，供应商与零售商之间构成非合作的序贯博弈关系，他们各自进行决策，目标都是使自身收益最大化。决策分两阶段进行，首先，由作为先决策者的供应商确定产品的寄售价格w 和寄售数量q;然后，零售商根据供应商给定的w 和q，确定产品的销售价格p。接下来，采用逆向归纳法来求解该模型。

2.1 零售商的销售价格决策

在分散决策的第二阶段，根据供应商在第一阶段确定的寄售价格w 和库存因子z，零售商的目标是选择最优的零售价格p 以最大化自身收益ΠD，R(p/w，z)，即:

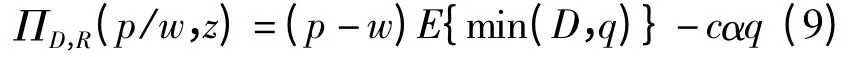
将q=y(p)z 代入式(9)得零售商的收益为:

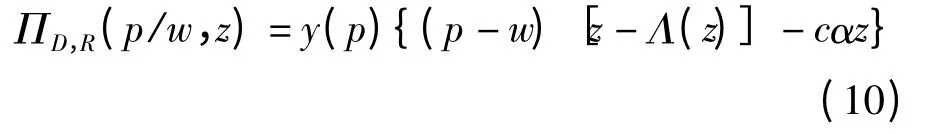
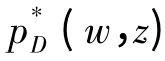
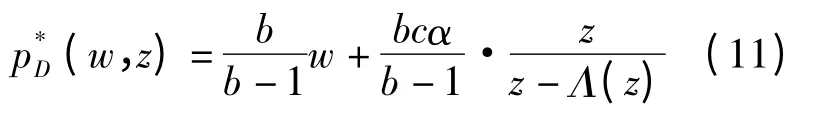
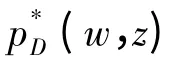
2.2 供应商的寄售价格和数量决策

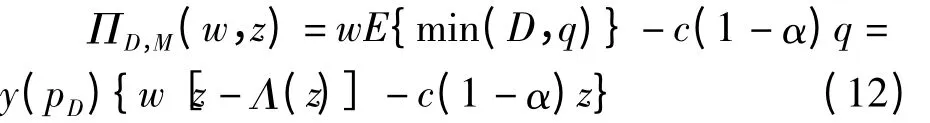
要求解使供应商期望收益ΠD，M(w，z)最大的(w，z)，首先就要求解对于任意给定的z，最优的寄售价格w*(z);然后再求解最大化期望收益ΠD，M(w，z)的z*。

由一阶条件∂ΠD，M(w，z)/∂w=0，可得供应商的最优寄售价格w*(z)为:

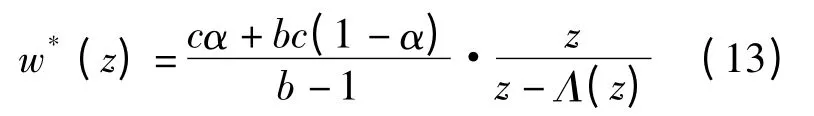
对于任意给定的z，当w ＜w*(z)时，有∂ΠD，M(w，z)/∂w ＞0;当 w ＞ w*(z)时，有∂ΠD，M(w，z)/∂w ＜0，因此w*(z)是使ΠD，M(w，z)最大的唯一值。由式(13)知:

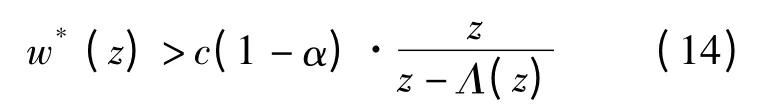
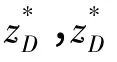
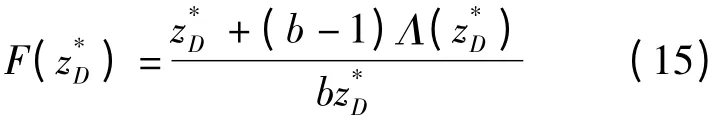
根据式(15)和式(6)可得:

将式(13)和式(15)代入式(11)有:

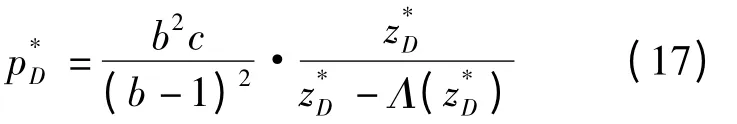
根据式(17)和式(5)有:

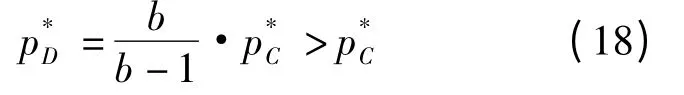
2.3 分散决策下的均衡收益

将式(13)、式(15)和式(17)分别代入式(10)和式(12)，可得零售商、供应商以及供应链整体在分散决策下的收益为:

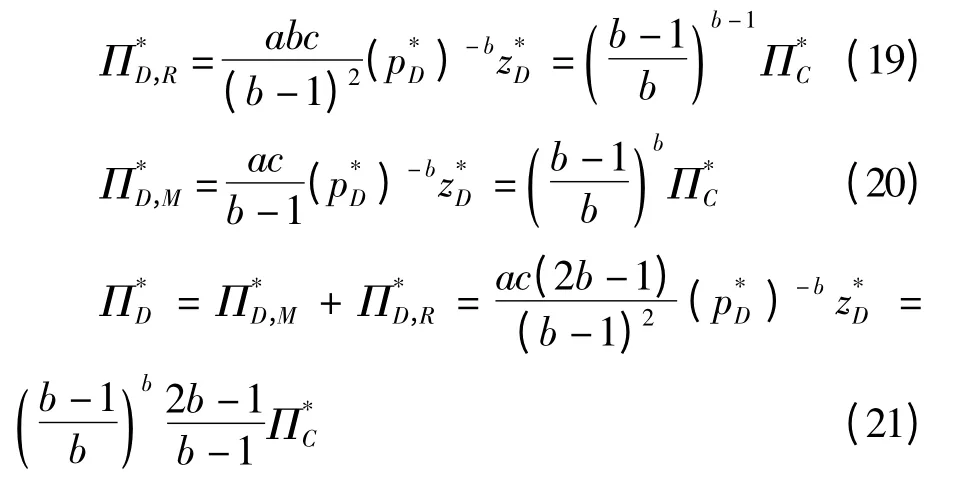
与集中决策相比，分散决策下的供应链收益损失率为:

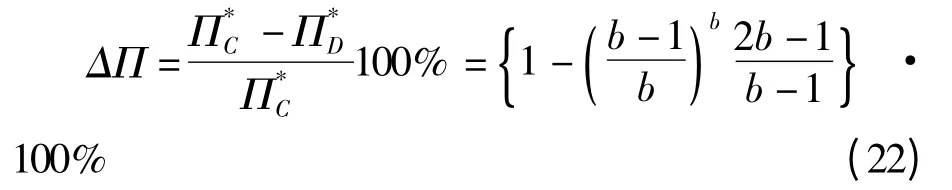
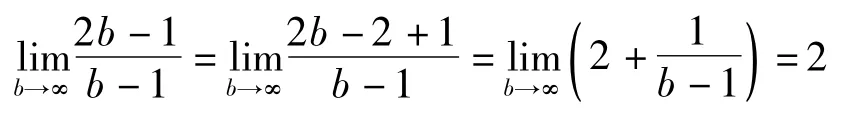
根据极限的四则法则可得:

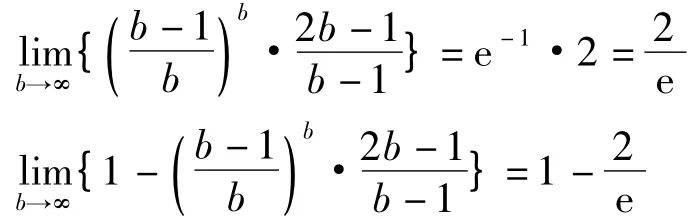
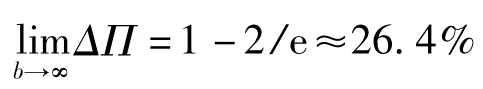
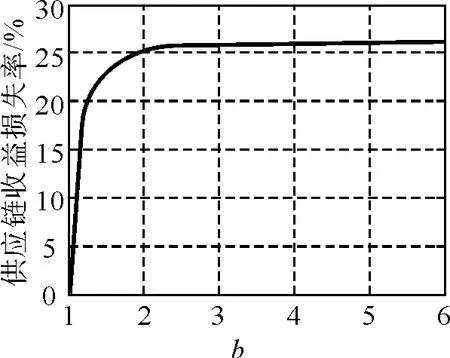
图1 供应链收益损失率ΔΠ 与b 的关系

推论1 分散决策下，基于批发价格的寄售契约，供应链的收益损失不会超过集中决策总收益的26.4%。

3 供应链协调

从以上分析可以看出，分散决策下的供应链总收益与集中决策相比总是有损失的。因此，考虑在寄售价格契约中引入旁支付来实现供应链协调，并运用Rubinstein 讨价还价模型求解供应链收益增量的分配比例和旁支付契约参数φ，解决了文献［13］未考虑的供应链收益增量分配合理性和公平性的问题。

在基于寄售价格的旁支付契约(w，φ)的条件下，零售商和供应商的收益分别为:

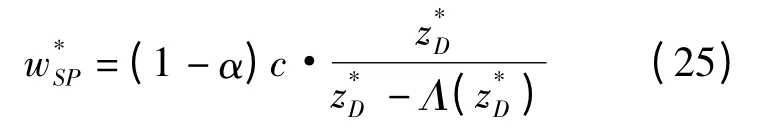
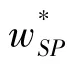
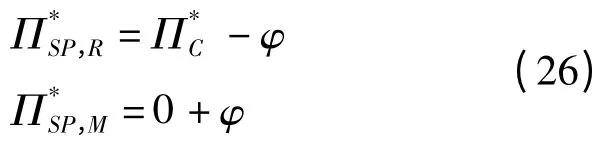
接下来，要解决如何设计参数φ 才能使旁支付契约具有合理性和公平性的问题。LENG 和ZHU 指出对于“二人非零和博弈”的收益增量分配问题，通常是运用纳什谈判解和夏普利值来求解。用这两种方法得出的结论是，供应链收益增量应该在供应链成员之间平均分配。而何龙飞等采用Rubinstein 讨价还价模型求解供应链收益增量的分配问题。与纳什谈判解不同的是，在Rubinstein 讨价还价模型中，收益增量的分配不是在供应链成员之间平均进行，而是取决于谈判双方的耐心程度和实力强度。与纳什谈判解和夏普利值相比，Rubinstein 讨价还价模型更接近现实。因此，笔者采用Rubinstein 讨价还价模型来求解参数φ。

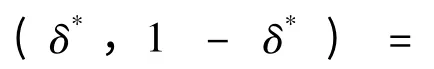
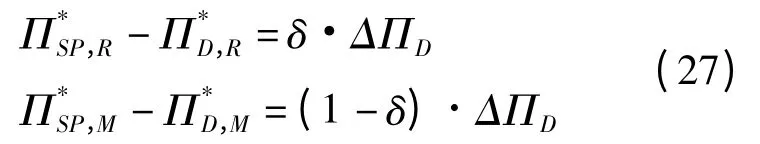
求解式(27)可得:

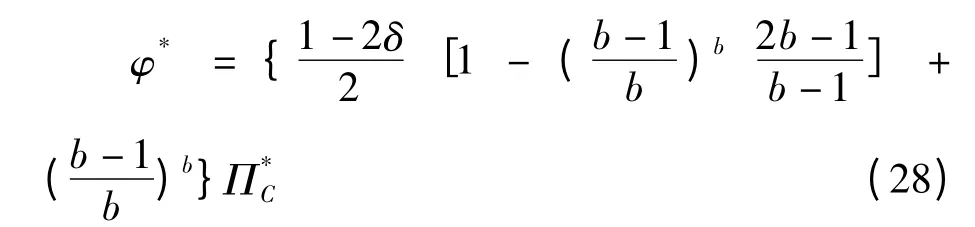
4 结论

笔者在文献［15］的基础上，建立了VMCI 寄售价格契约下的序贯博弈模型，分别求解了其在集中决策和分散决策情形下的最优决策和均衡收益。结果表明，与集中决策相比，分散决策下的系统收益损失最大可达到26.4%。对于分散决策下的供应链收益损失，通过引入旁支付可以完全实现供应链协调。最后，运用Rubinstein 讨价还价模型求解了双方的收益分配比例，解决了已有相关文献未能有效考虑的供应链收益增量分配的合理性和公平性问题。

［1］ ZHAO D，FANG M. The key of network manufacturing:integrating material，information，capital and knowledge flows［C］//The Proceedings of the 7th Annual International Manufacturing Symposium. Cambridge:［s.n.］，2002:1276－1283.

［2］ 黄庆扬，陈俊芳. 基于可控提前期的随机寄售库存模型［J］.管理工程学报，2010，24(1):138－145.

［3］ RUBIN P A.CARTER J R.Joint optimality in buyersupplier negotiations ［J］. Journal of Purchasing and Materials Management，1990，26 (2):20 –26.

［4］ CACHON G. Supply chain coordination with contracts［M］.Netherlands:［s.n.］，2003:229－340.

［5］ LARIVIERE M，PORTEUS E. Selling to the newsvendor:an analysis of price－only contracts［J］. Manufacturing ＆ Service Operations Management，2001，3(4):293－305.

［6］ CACHON G P，LARIVIERE M A.Supply chain coordination with revenue－sharing contracts:strengths and limitations［J］. Management Science，2005，51 (1):30－44.

［7］ TAYLOR T A.Supply chain coordination under channel rebates with sales effort effects［J］. Management Science，2002，48 (8):992－1007.

［8］ BERNSTEIN F，FEDERGRUEN A.Decentralized supply chains with competing retailers under demand uncertainty［J］.Management Science，2005，51 (1):18－29.

［9］ LENG M，ZHU A. Side－payment contracts in two－person nonzero－sum supply chain games:review，discussion and applications［J］.European Journal of Operational Research，2009，196(2):600－618.

［10］何龙飞，赵道致，刘阳.基于自执行契约设计的供应链动态博弈协调［J］. 系统工程理论与实践，2011，31(10):1864－1878.

［11］ WANG Y，JIANG L，SHEN Z. Channel performance under consignment contract with revenue sharing［J］.Management Science，2004，50(1):34－47.

［12］WANG Y.Joint pricing－production decisions in supply chains of complementary products with uncertain demand［J］.Operations Research，2006，54(6):1110－1127.

［13］ZHANG D，MATTA R，LOWE T J. Channel coordination in a consignment contract［J］. European Journal of Operational Research，2010，207(2):897－905.

［14］ LI S，HUA Z. A note on channel performance under consignment contract with revenue sharing［J］. European Journal of Operational Research，2008，184(2):793－796.

［15］ RU J，WANG Y. Consignment contracting:who should control inventory in the supply chain?［J］. European Journal of Operational Research，2010，201(3):760－769.

［16］ PETRUZZI N，DADA M. Pricing and the newsvendor problem:a review with extensions［J］.Operations Research，1999，47 (2):184－194.

［17］ADIDA E，RATISOONTORN N.Consignment contracts with retail competition［J］.European Journal of Operational Research，2011，215(1):136－148.

［18］张维迎.博弈论与信息经济学［M］.上海:上海人民出版社，1996:119－123.

［19］黎诣远. 微观经济分析［M］. 北京:清华大学出版社，1996:131－137.