双渠道供应链中售后服务横向合作策略

陈远高，郭燕翔

(浙江财经学院 信息学院，浙江 杭州310018)

随着Internet 电子商务应用的普及，采用双渠道供应链战略的厂商日渐增加。网络渠道信息传递便捷，菜单成本低廉，商品陈列不受物理空间限制，但网络的虚拟性使消费者对在线商品缺乏实际体验和感触，导致众多消费者望而却步［1］。而传统渠道凭借其具有实体场所和一对一人员服务的优势，在商品体验以及物理性服务方面具有优势［2］。因此厂商往往通过传统渠道和网络渠道间的服务合作实现不同渠道的优势互补［3－4］。

在已有的双渠道供应链研究文献中，研究焦点主要集中在厂商的渠道选择、渠道竞争，以及供应链纵向的契约协调方面。近年来，随着消费者对于网络购物的追捧，研究者开始关注双渠道供应链中存在的渠道横向合作问题。按照已有研究中渠道横向合作模式的不同，可以分为以下3 种:①需求推荐合作模式。CHEN 将其定义为在线的信息中介商向零售商提供需求推荐的合作模式［5］;肖剑等研究了渠道间的需求转让合作带来的供应链协调问题［6］。②库存与配送合作模式。SEIFERT 等提出传统销售渠道中的多余库存通过网络直销渠道进行销售［7］;张波和黄培清在此基础上将其拓展到网络零售商向传统零售商进行顾客推荐而传统零售商负责商品配送和货款回收的模式［8］。③一般服务合作模式。YROJOLA 研究了服务替换成本对双渠道间消费者转化的影响［9］;肖剑等讨论了制造商直销渠道与零售渠道之间服务合作导致的服务定价问题［10］。与已有研究不同，笔者考虑了一类存在售后服务横向合作的双渠道供应链系统，网络零售商进行在线的产品零售，而售后服务环节由传统零售商承担，形成基于售后服务的渠道服务横向合作模式。

1 模型建立

假设网络零售商通过其在线商店进行产品的销售，由于不具备实体店铺和售后服务人员，网络零售商将其产品的售后服务外包给具有服务能力的传统零售商负责，并与传统零售商订立{s，t}的契约，即传统零售商为客户提供服务水平s 的售后服务，而网络零售商则向传统零售商支付t 单位的服务费用，供应链系统模型如图1 所示。

图1 存在服务横向合作的双渠道供应链系统

假设网络零售商和传统零售商均能按照批发价格w 从制造商处采购产品进行销售，借鉴BANKER 等［11］和杨树等［12］的模型，双渠道需求函数可以表示为:

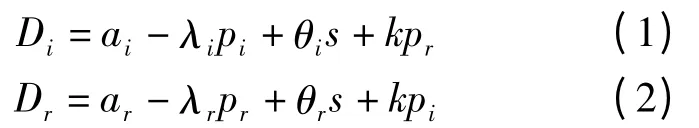
其中:ai、ar分别为网络渠道与传统渠道的市场规模(ai，ar＞0);λi、λr分别为双渠道中产品价格敏感程度(λi，λr＞0);pi、pr分别为双渠道中产品零售价格;k 为渠道之间的需求替代性与价格竞争程度(0≤k ＜1);θi、θr分别为双渠道消费者对于售后服务的敏感程度(θi，θr＞0);s 为渠道提供的售后服务水平。传统零售商的服务成本为ηs2/2，η 为服务成本系数。不考虑传统零售商服务能力限制的问题，通过其已有的售后服务网络提供服务，则不存在成本的增加。

网络零售商和传统零售商的利润函数Πi、Πr可以表示为:

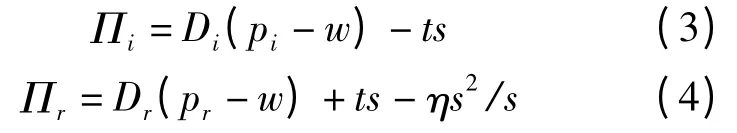
为了分析简单，假设网络零售商与传统零售商的销售成本为零，网络零售商和传统零售商从制造商处采购的产品批发价格为零，消费者对产品价格的敏感程度λi，λr=1，0≤k ＜1。

2 供应链Stackelberg 博弈均衡分析

假设网络零售商为Stackelberg 博弈的领导者，决定网络零售价格pi和愿意支付的服务费用t，传统零售商决定零售价格pr和服务水平s。由利润最大化条件可以得到:

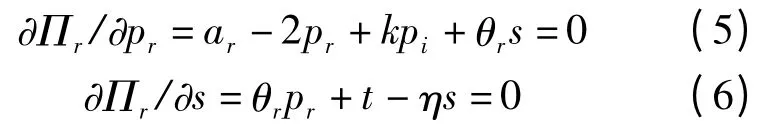
二阶条件的Hessian 矩阵为:

将pi、t 的值代入式(5)和式(6)可得到:

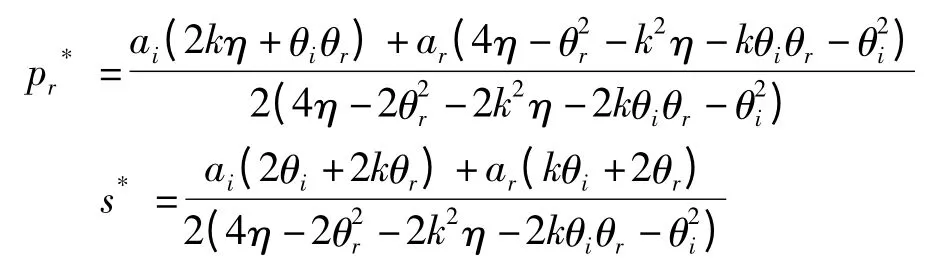
此时，网络零售商与传统零售商的最大利润分别为:

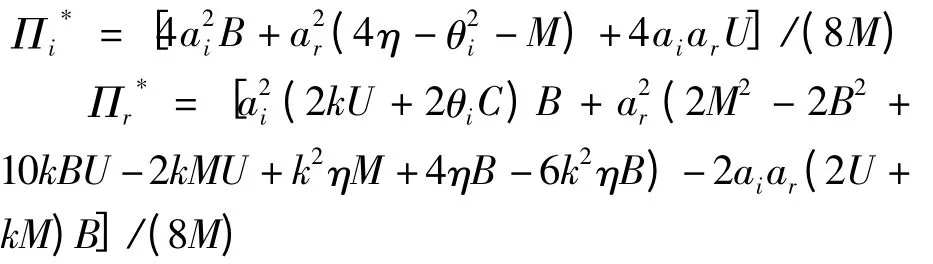
命题1 当存在服务横向合作的双渠道供应链系统达到Stackelberg 均衡时，双渠道供应链存在以下特征:

(1)双渠道供应链的定价、服务水平、服务外包佣金、利润随网络市场与传统市场规模(ai、ar)的增加而递增。市场规模越大，网络零售商与传统零售商可获得最优定价越高，服务水平越高，网络零售商愿意支付的服务外包佣金越高，二者可获得的利润越大。

(3)当两种渠道的市场规模相等(ai=ar)且传统零售商的服务成本系数固定时，双渠道供应链的最优定价和服务水平随着两种渠道中服务敏感程度的增加而提高。

证明:

(1)当供应链系统达到Stackelberg 博弈均衡时，容易证明ai、ar与各决策变量取值为单调递增关系。命题1 中的特征(1)得证。

(2)当ai=ar，令ai=ar=a，可以得到∂pi*/∂η=［－ (2 + k)aC2－(2－k2)aθrC］/M2，因为0≤k ＜1，C ＞0，所以∂pi*/∂η ＜0。同理可证pr*、t*、s*及Πi*与η 均为单调递减关系。命题1 中的特征(2)得证。

(3)∂pi*/∂θi= ［(4C + 2θr)aB + (θiU +2kηC)a］/(2M2)，因为U ＞0，B ＞0，C ＞0，所以有∂pi*/∂θi＞0，可得pi*与θi为单调递增关系，同理可证pr*、pi*、s*与θi、θr之间均为单调递增关系。命题1 中的特征(3)得证。

综上，命题1 得证。

证明:令ai=ar=a，可以得到:

3 算例分析

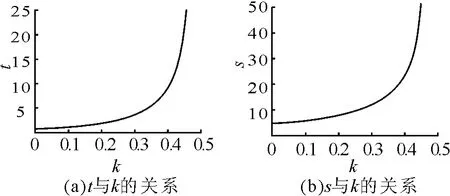
图2 渠道竞争程度与服务费用、服务水平的关系

设k=0.2，即网络渠道与传统渠道间的需求替代性和竞争程度较弱，渠道服务敏感程度与渠道最优定价、渠道服务水平的关系如图3 所示。

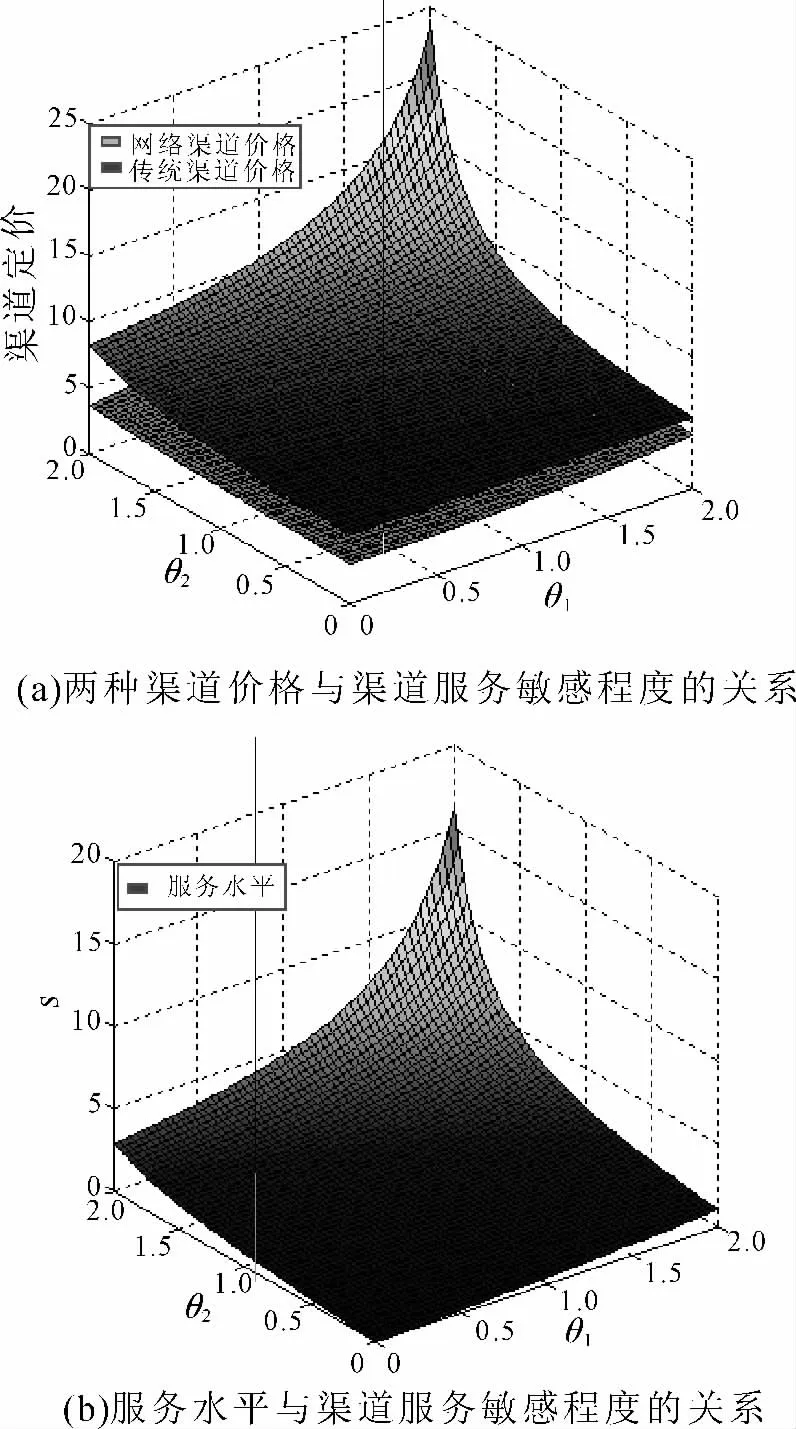
图3 渠道服务敏感程度与渠道定价、服务水平的关系

由图3 可知，在渠道双方都可以获得正利润的前提下，双渠道中的产品最优定价与横向合作的服务水平均随双渠道服务敏感系数的递增而增加。说明随着网上购物的成熟，消费者对于网络购物的售后服务质量必将越来越重视，网络零售商需采取有效措施来改善和提高服务水平及质量，从而获得更高的产品定价，并能使合作双方都能从中获取更多利润。假设网络零售商独立提供售后服务的成本要高于传统零售商，令ηi=3，ηr=2，双渠道供应链的利润分配与渠道竞争程度的影响关系如图4 所示。

图4 渠道竞争条件下横向服务合作与供应链利润关系

从图4 可知，在渠道间缺乏竞争的条件下，服务合作对于传统渠道的影响作用不明显，但却能够有效提升网络渠道的利润水平。随着渠道间需求替代性与竞争程度的加剧，供应链双方均能从横向的服务合作中受益，且传统零售商利润增长趋势要快于网络零售商，充分说明横向服务合作有利于服务资源的优化配置与应用。

4 结论

笔者考虑了双渠道供应链系统中的售后服务横向合作模式，建立了双渠道供应链的服务横向合作模型，分析了Stackelberg 博弈中网络零售商与传统零售商的最优渠道服务、最优定价和供应链的利润分配，以及相关参数对决策变量的影响。结果表明，供应链渠道间的售后服务合作有利于供应链系统资源的优化配置，但服务合作效果受到渠道市场规模、渠道间竞争程度，以及消费者服务敏感程度的影响。

［1］ COUGHLAN A T，ANDERSON E，STERN L W，et al.Marketing channels［M］.Upper Saddle River:Prentice Hall，2001:65－134.

［2］ BITNER M J，BROWN S W，MEUTER M L.Technology infusion in service encounters［J］.Journal of the Academy of Marketing Science，2000，28(1):138－149.

［3］ PHILIP J T，SWINDER J.How do consumers evaluate internet retail service quality?［J］. The Journal of Services Marketing，2003，17(2/3):243－248.

［4］ YUAN X，DAVID B G.Developing a framework for measuring physical distribution service quality of multi－channel and "pure player" internet retailers［J］.International Journal of Retail ＆ Distribution Management，2006，34(4/5):278－286.

［5］ CHEN Y，IYER G，PADMANABHAN V.Referral infomediaries［J］.Marketing Science，2002，21(4):412－434.

［6］ 肖剑，但斌，张旭梅.双渠道供应链电子渠道与零售商合作策略研究［J］. 系统工程学报，2009，24(6):673－679.

［7］ SEIFERT R W，THONEMANN U W，SIEKE M A.Integrating direct and indirect sales channels under decentralized decision－making［J］.International Journal of Production Economics，2006，103(1):209－229.

［8］ 张波，黄培清.虚拟供应链的Internet 零售商交付渠道选择［J］.工业工程与管理，2008，13(1):27－30.

［9］ YROJOLA H.Physical distribution considerations for electronic grocery shopping［J］.International Journal of Physical Distribution ＆ Logistics Management，2001，31(10):746－761.

［10］肖剑，但斌，张旭梅.双渠道供应链中制造商与零售商的服务合作定价策略［J］.系统工程理论与实践，2010，30(12):2203－2211.

［11］BANKER R D，KHOSLA I，SINHA K K. Quality and competition［J］. Management Science，1998，44(9):1179－1192.

［12］杨树，杜少甫，梁樑，等. 旅游供应链最优服务质量决策［J］.管理科学学报，2009，12(3):37－43.