基于序列比对方法的股市波动实证研究

徐 梅，刘秀秀

(天津大学 管理与经济学部，天津300072)

股价波动反映了金融市场风险的变化，采用科学的方法预测股价波动对于风险管理、风险规避具有重要的意义。目前国内外关于股价波动的研究方法主要有两大类:一类是金融计量学的研究方法，包括广义自回归条件异方差(GARCH)类模型和随机波动(SV)类模型［1］等，另一类是混沌等非线性系统的理论和方法［2］。目前大多数方法着重预测股价未来具体的波动值，其模型选择的关键是要使预测值与真值之间的数量误差最小化。但人们有时可能更关心未来风险所处的等级，希望通过对波动等级或波动所处区间的预测达到预测风险、规避风险的目的。笔者将符号时间序列方法与生物信息学中的序列比对方法引入到股价波动的预测中，提出一种新的股价波动预测方法，该方法既可预测波动值，又可预测波动等级。

序列比对是生物信息学中一种基本的信息处理方法［3］，虽然序列比对方法在金融时间序列之间的相似性分析中得到少量应用［4］，但在股价波动的预测中还未见报道。笔者采用符号化方法将股价波动时间序列转化为符号序列，这样就与生物学中的残基有相似的模式，即符号的个数与残基的数目都是确定的，可以一一设定相似比对分值，从而可以用序列比对方法对两个波动序列进行相似性度量，进而利用K－近邻法实现对股价波动的预测。

1 时间序列符号化

时间序列符号化，就是根据一定的规则设置阈值函数，将有许多不同值的时间序列转化为仅有几个互不相同符号的序列［5］。符号化的目的是简化系统，捕获时间序列大尺度的特征，从而降低噪声的影响。将时间序列符号化的步骤为:根据一定的规则将时间序列划分为有限个区间，每个区间分配不同的符号。若共有n 个符号，则符号集大小为n，根据每个数据落入区间的不同，将时间序列转换成由一系列离散化的符号组成的符号序列［6］。

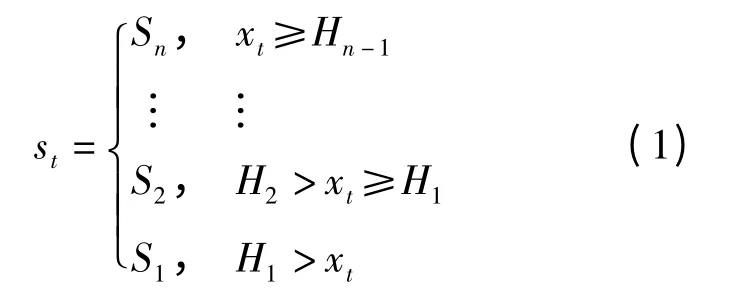
2 序列比对

2.1 序列比对问题描述

序列比对是运用某种特定的数学模型或算法，找出两个或多个序列之间的最大匹配碱基或残基数［7］，通过插入适当的空位来模拟基因序列中的突变现象，寻找序列间的相似区域。空位引入有生物学的依据，它意味着两个序列有残基的插入与缺失。而空位插入也有较好的经济学意义，它改变了原始序列中符号所处的位置，允许经济效应传播过程中时延的存在，这是对单纯计算两个序列中相对应数值相似程度的重大突破与改进。

序列比对问题可以表示为MSA =(Σ′，Q，A，F)，其中:

(1)Σ′ =Σ∪{－}为序列比对的符号集;－表示空位;Σ 为基本字符集，对于DNA 序列，Σ ={a，c，g，t}代表4 个碱基，对于符号时间序列{st，t=0，1，…，N－1}，Σ ={S1，S2，…，Sn}代表n 个符号，st与Si满足式(1);

(2)Q={Q1，Q2，…，QT}为序列集，其中Qi=(ci1，ci2，…，ciLi)，cij∈Σ，Li为第i 个序列的长度;

(3)矩阵A =(aij)T×D，(D≥max{L1，L2，…，LT})，aij∈Σ′为序列集Q 的一个比对结果，其中:矩阵的第i 行为参与比对的第i 个序列的扩张序列(即插入空位的序列，如果移去所有的－将得到原来的序列);矩阵中的每一列不允许同时为－;

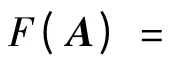
(5)序列比对问题MSA 就是通过插入适当的空位，构建出一个使得相似性度量函数F(A)达到最大的比对A［8］。

空位的引入有着重要的作用，但如果对引入空位的数目不加以限制，即使匹配得分再高也可能没有意义。因此必须对空位进行罚分，以限制引入空位的数目。罚分包括起始空位罚分和延伸空位罚分，通常采用线性罚分函数g(k)=－kd或仿射罚分函数g(k)=－d－(k－1)b(d ＞0)来对空位进行罚分，其中k 为空位个数，d 为初始罚分，b 为延伸罚分。

2.2 计分函数

在进行序列比对时，传统的计分方法将匹配的数据计为1 分，不匹配的数据计为0 分，然而在经济领域中，为了反映经济指标趋势变化的强弱，对于长度为n、m 的序列Z = {Z1，Z2，…，Zn}和T={T1，T2，…，Tm}，计分函数可表示为:

sc(Zi，Tj)为元素Zi和Tj的相似性得分值。对于不同的研究对象可以采用不同的计分函数以获得更多信息。

设序列Z′和T′为在序列Z 和T 中插入空位后得到的扩展序列，序列比对就是把序列Z′和T′上下罗列起来，相应的位置进行一一比较。两个序列比对后的相似性总得分为:

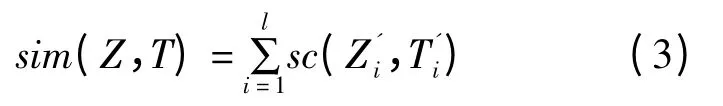
其中:l≤|Z′| + |T′| ，|Z′|、|T′|分别为序列Z、T 扩展序列Z′、T′的长度。

2.3 动态规划算法

Needleman－Wunsch 算法是基于动态规划的全局比对算法。对于长度分别为n、m 的序列Z和T，其比对过程可用一个以序列Z 为最左边一列，T 为最上面一行的(n+1)×(m+1)得分矩阵M 来表示。初始化得分矩阵M 为:M1，1= 0，Mi，1=－id，M1，j=－jd，Mi，j为矩阵中第i 行，第j列元素的最优匹配得分［9］，递归计算式为:

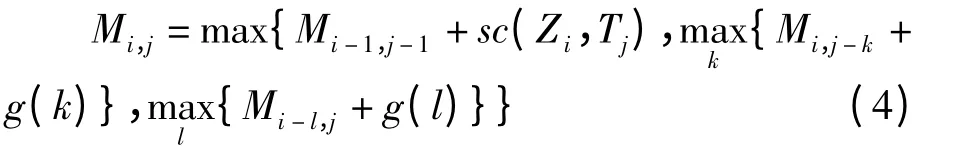
其中:1 ＜i≤n+1，1 ＜j≤m +1，1≤k ＜j，1≤l ＜i，d 为初始罚分，g(k)=－kd 为连续k 个空位的罚分。Mn+1，m+1为Z 和T 两个序列全局比对的相似性总得分，因此从矩阵M 最右下角的单元到左上单元回溯最佳路径，可找到最优联配结果。从最大的右下角元素开始回溯可以得到最优匹配序列，而从次大的元素开始回溯可以得到次优匹配序列，以此类推。若联配得分矩阵M 中的箭头为对角线，则序列Z 和序列T 中的两个数据相对应;若箭头为水平方向，则在序列Z 的相应位置插入一个空位;若箭头为垂直方向，则在序列T的相应位置插入一个空位。因为可以插入多个空位，所以最优比对结果可能不唯一。

3 基于K－近邻法的股价波动预测

K－近邻法的基本思想是在多维空间中找到与未知样本最近邻的K 个点，这K 个点就是未知样本的K 个最近邻，可以根据这K 个最近邻的数据特征对未知样本进行预测。实际度量中常用欧氏距离d(x，y)=‖x－y‖来描述各样本之间的相似性程度［10］。笔者为了预测股价波动值及波动区间，不采用距离函数刻画样本相似性程度，而是采用序列比对方法中式(3)所示的相似性总得分sim 作为度量指标。进而在整个样本序列中找出与比对目标序列较优匹配的K 个子序列，根据这K 个子序列的后续值或符号即可得到比对目标序列下一时点波动值或波动区间的预测。

笔者通过设置相似性总得分sim 的阈值q 来确定K，阈值q 越大，查询到匹配的子序列越少，K越小;反之q 越小，查询到的子序列越多，K 越大。

3.1 波动值预测步骤

(1)设波动时间序列为{Vt，t=1，2，…，N}，待预测波动值为VN+1，依据时间序列符号化方法将{Vt}转换为波动符号序列{SVt，t=1，2，…，N}。

(2)将符号序列{SVt，t =1，2，…，N}分割成m 维的向量:

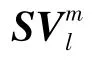
(4)依据相似性总得分计算每个最近邻的权重ωj为:

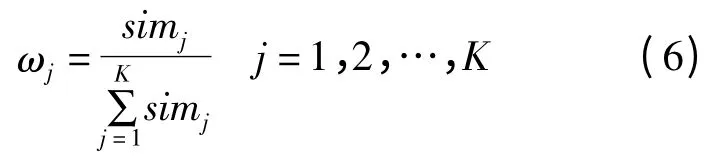
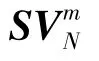
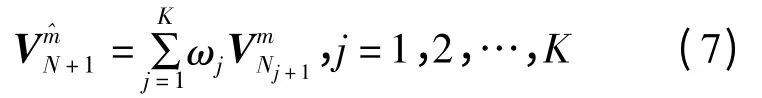
3.2 波动区间预测步骤

(1)设波动时间序列为{Vt，t =1，2，…，N}，依据时间序列符号化方法将其转换为波动符号序列{SVt，t =1，2，…，N}，设符号集大小为n，对应的符号为{Si，i =1，2，…，n}，待预测波动符号为SVN+1。

步骤(2)～步骤(4)同波动值预测步骤。

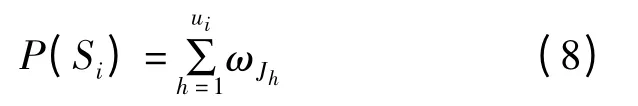
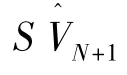
4 实证分析

笔者以上海证券交易所综合指数(简称上证综指)和深圳证券交易所成分股价指数(简称深证成指)2010 年1 月—12 月，采样间隔为20 min的高频数据为样本数据，上午9:30—11:30 和下午13:00—15:00 是连续竞价时间，每天交易时间为4 h，则每日有12 个数据，确定K－近邻法中的嵌入维数m 为12，从2010 年1 月4 日至2010 年12 月31 日共有2 904 个数据。以2010 年11月—12 月的540 个数据为待预测数据，比较股价波动的实际值与预测值，从而验证基于序列比对的股价波动预测方法的有效性。

设Pt为t 时刻的价格，则收益Rt可表示为:

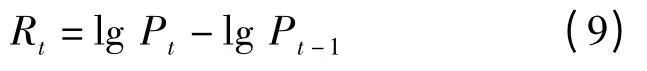
波动Vt定义为:

4.1 时间序列符号化

对于上证综指和深证成指的波动时间序列{Vt}，采用符号化方法，将其转化为符号序列{SVt}。取符号集大小n=5，5 种符号分别用－2、－1、0、1、2 表示，由弱到强依次对应5 种不同的波动等级。设置各个符号出现的概率向量为{15%、20%、30%、20%、15%}，根据式(1)进行符号化，其中的各百分位数如表1 所示。例如，当上证综指Vt∈［4.37 ×10－7，2.39 ×10－6］时，SVt=－1。

表1 波动时间序列的符号划分区间

4.2 股价波动值预测

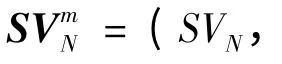
以预测上证综指2010 年11 月1 日第一个波动值为例，则2010 年10 月29 日的符号序列{0，0，1，1，2，－2，0，－1，1，0，0，－2，2}为比对目标序列。将比对目标序列放在矩阵最左边一列，比对样本序列中的某一向量放在矩阵最上面一行，计算联配得分矩阵。首先根据式(2)计算计分矩阵，然后根据式(4)计算全局比对中联配得分矩阵M 的最右下角元素并回溯出联配序列，较大的K 个元素所对应的联配序列即为比对目标序列的K 个最近邻。该例有一个最大得分6 分，4 个次大得分5 分及7 个得分4 分，其中最大得分6 分所对应的联配得分矩阵如图1 所示。

1 2010 年10 月29 日上证综指最优联配得分矩阵

最优联配结果如下:

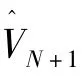
图2 2010 年11 月—12 月上证综指波动时间序列实际值与预测值曲线

为检验该方法的预测效果，引入MAPE 度量指标，MAPE 值即为平均相对误差绝对值，计算公式为:

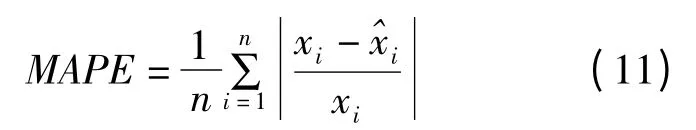
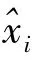
如果MAPE 值低于10%，则认为预测精度较高。利用上述方法计算上证综指和深证成指的波动时间序列MAPE 指标值，分别为3. 86%、4.07%，MAPE 值均低于5%，可见使用符号化序列比对方法来寻找历史上相似的子序列，进而预测今后时间序列值的效果较好。

4.3 股价波动区间预测

按照波动区间的预测步骤可得出2010 年11月—12 月540 个波动符号的预测值，将上证综指和深证成指的实际符号与预测符号分别进行比较，符号完全相同(如2 和2)的比例为32.04%、31.30%，符号相差1 级(如－1 和0)的比例为49.81%、47.04%，符号相差2 级(如－2 和0)的比例为9.44%、13.33%，符号相差3 级(如－1 和2)的比例为6.30%、5.37%，符号相差4 级(仅－2和2)的比例为2.41%、2.96%。可见实际值和预测值对应相同或相近(仅指相差一级)符号的比例为81.85%、78.34%，说明波动区间相同或相近的比例较高，预测效果较好。根据符号值来判断波动的强弱，不关注具体的波动数值，而从大尺度的角度确定波动所处的区间，以判断未来风险所处的等级。

5 结论

笔者将符号时间序列分析方法与生物信息学中的序列比对方法引入股价波动的预测中，可以捕获时间序列的非线性特征，降低噪声的敏感性，也不用做出数据是否平稳等假设，预测的结果不仅包括未来具体的波动值，也包括波动的等级或波动所处的区间。实证研究表明，该方法预测能力较强，适用范围广泛，验证了序列比对方法应用于金融领域的可行性。

［1］ BORDIGNON S，CAPORIN M，LISI F.Generalised long－memory GARCH models for intra－daily volatility［J］.Computational Statistics ＆ Data Analysis，2004，51(12):5900－5912.

［2］ 刘军，邱晓红，汪志勇，等.基于相似性最优模块神经网络的股票预测［J］.江西师范大学学报:自然科学版，2008，32(4):443－448.

［3］ 应嘉，赵睿，尚彤.生物信息学在人类基因计划中的应用［J］.北京大学学报:医学版，2002，34(4):389－ 392.

［4］ TAKUYA Y，KODAI S，TAISEI K，et al.Symbolic analysis of indicator time series by quantitative sequence alignment［J］.Computational Statistics and Data Analysis，2008(53):486－495.

［5］ 马东玲.符号时间序列分析在睡眠脑电中的应用［J］.微计算机信息，2010，26(10－1):231－232.

［6］ DAWC S，FINNEY C E A，TRACY E R. A review of symbolic analysis of experimental data［J］.Review of Scientific Instruments，2003(44):915－930.

［7］ 张永，王瑞.生物信息学中的序列比对算法［J］. 电脑知识与技术，2008(1):181－184.

［8］ 张敏.生物序列比对算法研究现状与展望［J］.大连大学学报，2004，25(4):45－48.

［9］ NEEDLEMAN S B，WUNCH C D. A general method applicable to the search for similarities in the amino acid sequence of two proteins［J］.Journal of Molecular Biology，1970(48):443－453.

［10］许东，代力民，邵国凡，等.基于RS、GIS 及k－近邻法的森林蓄积量估测［J］.辽宁工程技术大学学报，2008，24(2):195－194.

［11］ JAYAWARDENA A W，LI W K，XU P. Neighbourhood selection for local modeling and prediction of hydrological time series［J］.Journal of Hydrology，2002，258(1－4):40－57.