一类基于动态优化问题的混沌猴群算法

齐艳玉，兰燕飞

(天津大学 系统工程研究所，天津300072)

一些性能优异的启发式智能算法，如遗传算法(GA)［1－4］、粒子群算法(PSO)［5］和人工神经网络(ANN)［6－7］等在很大程度上增强了人类对复杂优化问题的求解能力，已在各个领域得到了广泛应用。但这些算法几乎毫无例外地都很难逃脱所谓的“维数灾难”问题，在实际应用中也受到诸多限制。2008 年ZHAO 和TANG［8］提出一种新的用于求解大规模、多峰优化问题的智能优化算法，即猴群算法(MA)。随后，郝士鹏［9］结合猴群算法和混沌搜索技术，提出了混沌猴群算法(CMA)。基于混沌的遍历性及不重复性而提出的混沌搜索技术比传统的随机搜索技术速度更快，质量更高，将混沌搜索技术引入到MA 中在很大程度上避免了猴群算法陷入局部最优。作为一种智能算法，MA 及其改进算法能够有效地求解高维、非线性不可微的函数优化问题，并且MA 需要调整的参数也少，这使得MA 易于实现，具有广阔的应用前景。文献［10］在利用模糊模拟技术来估计目标函数中模糊事件可信性的基础上设计了基于模糊模拟的猴群算法来对无约束优化问题进行求解，并获得了原模糊约束满足问题的约束一致解。文献［11］针对项目进度问题的模糊相关机会规划模型设计了猴群算法的模糊模拟求解方法。文献［12］针对入侵检测系统存在高漏报率的问题，提出了一种基于猴群算法的入侵检测技术，改进了生成规则的质量，提高了入侵检测系统的检测率。文献［13］结合输电网扩展规划问题的特点提出了求解含有离散变量优化问题的离散猴群算法(DMA)。然而，由于MA 出现的时间较短，对MA 及其改进算法的应用研究还较少。笔者拟设计一种适用于求解动态规划问题的智能算法，鉴于CMA 在问题求解的性能方面更优于MA，因此，选用CMA 设计了求解一类动态规划问题的混沌猴群算法。

1 一类动态优化问题的模型

动态优化问题广泛存在于工程实际和日常生活中，其最优解会因为目标函数、环境参数或者约束条件的变化而随时发生变化，因此，在解决这些动态优化问题时，需要一类功能强大的智能算法对变化做出准确响应，并及时地做出新环境下的最优或满意决策。

目前，对动态优化问题的求解，一方面，由于实际系统的复杂性较难得到解析解，另一方面，借助计算机应用智能算法求解的研究很少，因此，需利用性能优越的智能算法去求解动态优化问题。

考虑如下一类动态优化问题的基本模型［14］:

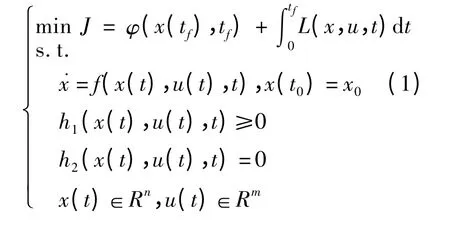
求解最优控制问题，传统方法包括变分法、最大(最小值)原理、动态规划等。对于一些复杂的实际问题，有时利用传统方法很难求得解析解，然而，实际应用中人们需要得到的往往只是一些阶段的数值解，因此，智能算法作为一种新的求解方法被用来帮助寻找数值解。

2 一类动态优化问题的混沌猴群算法

2.1 混沌猴群算法

猴群算法是一种新的用于求解大规模、多峰优化问题的智能优化算法，其思想在于通过模拟自然界中猴群爬山过程设计了爬、望和跳这3 个过程。郝士鹏结合猴群算法和混沌搜索技术提出了一种改进的、性能更加优越的猴群算法，称为混沌猴群算法CMA，主要包括混沌初始化、步长递减的爬过程、参数递增的混沌望过程和边缘跳过程4 个步骤。

2.2 模型的离散化处理

计算机所处理的数据是数字量，它不仅在数值上是整量化的，而且在时间上是离散化的，因此在利用CMA 进行求解之前，先对模型进行离散化处理。离散是按一个等样采样周期t 的采样过程处理，即将t 变为kt(k=0，1，2，…，为一正整数)。控制变量u(t)被认为仅在采样时刻发生变化，在相邻两采样时刻之间，u(t)是通过零阶保持器保持不变的，且等于前一采样时刻之值，即在kt 和(k+1)t 之间，u(t)=u(kt)=常数。式(1)通过离散化，可转化为如下形式［15］:

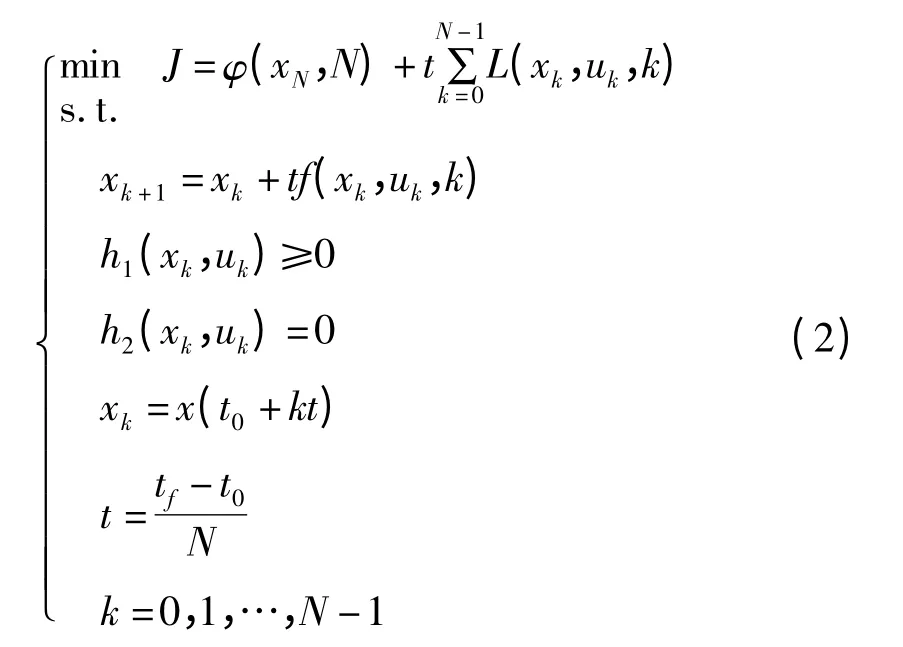
经离散化后，可以看出，原问题变为一个多维的优化问题，由于CMA 在求解多维优化问题上的优越性，因此可采用CMA 对其求解。

2.3 混沌猴群算法求解动态优化问题

(1)解的表示。令正整数M 为猴群的规模，xi=(xi1，xi2，…，xin)，i=1，2，…，M，xi表示第i 个猴子的当前位置，每只猴子的位置对应优化问题的一个决策向量。在式(2)中，决策向量为u =(u1，u2，…，uN)，令M =5，则向量ui= (ui1，ui2，…，uiN)，i=1，2，…，5，表示5 只猴子的位置，同时又可以视为式(2)的5 个解。

(2)混沌初始化。郝士鹏采用Logistic 函数y(k+1)=4y(k)(1－y(k))产生混沌变量来进行初始化，其中，y 为混沌变量，k 为迭代次数。但是Logistic 函数只有当初值y0∉{0.00，0.25，0.50，0.75}时，混沌变量y(k)的轨迹才可以遍历整个值域范围。笔者采用一个遍历性更好且没有初始值限制的混沌函数y(k+1)=sin 2/y(k)来对模型的解进行初始化。在值域［a，b］内产生混沌变量的步骤如下:①令k=0，且设置y(0)的初始值;②利用混沌函数y(k+1)=sin 2/y(k)产生下一次迭代后的混沌变量值;③利用线性变换公式u(k)=a +y(k)(b－a)将混沌变量的值域转换到优化问题的定义域内;④若达到规定最大迭代次数，则终止;否则，令k =k+1，返回步骤②。

uij(i=1，2，…，M，j=1，2，…，N)的初始值通过在［a，b］上循环迭代产生混沌变量。

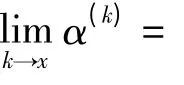
(4)参数递增的混沌望过程。经过爬过程之后，每只猴子都达到了各自所在山峰的顶处，即目标函数达到了局部最优。望过程是用来观察周围邻近区域是否存在比当前位置更高的山峰，若存在，则跳过去。CMA 设计了一种逐渐递增的视野参数β 与递增的望时间ω 来达到算法的收敛速度和解的质量与CPU 的耗费时间的平衡:β(k+1)=ρβ(k)，ω(k+1)=φω(k)，其中，ρ 和φ 为递增因子，k 为循环次数。

(5)边缘跳过程。假设经过望过程后猴子已经不能在其视野范围内找到更好的位置，边缘跳过程的主要目的在于搜索由当前区域转移到新的区域，猴子跳的方向为沿着指向猴群支点的方向跳到视野的最边缘处。

(6)终止。经过步长递减的爬过程、参数递增的混沌望过程和边缘跳过程之后，完成了一次完整的循环，在达到预设的循环次数之后，CMA将终止。

3 数值算例

考虑如下例子:

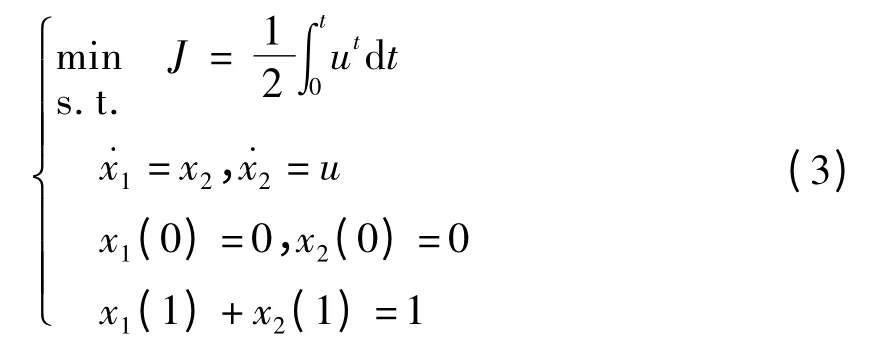
对式(3)求解的CMA 用C + +语言实现，参数的设置见表1，结果见表2。

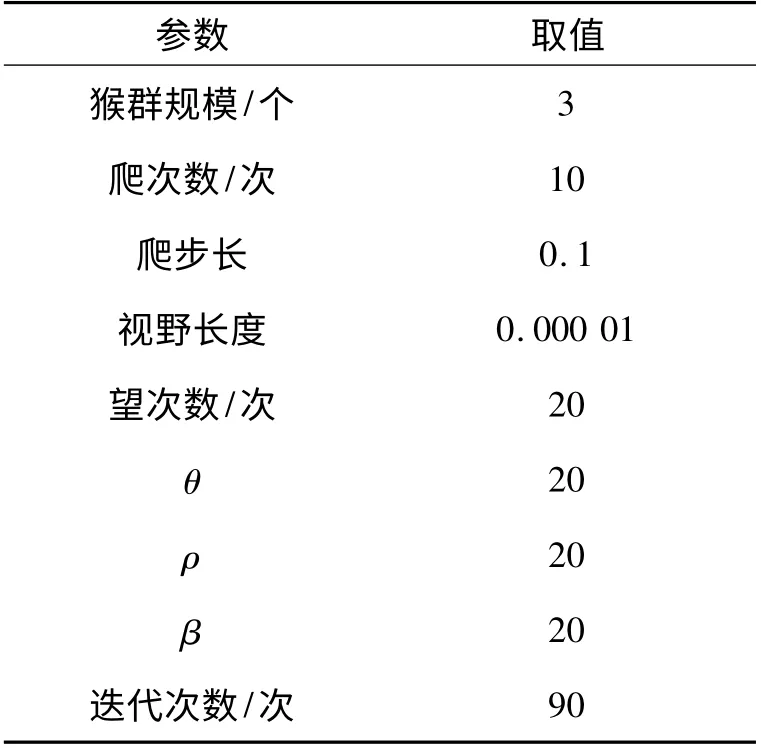
表1 CMA 的参数

表2 例子的结果

J 的最优值为0，由表2 可以看出，用CMA 计算出的结果非常接近最优值，并且N 越大，结果越精确，可以根据实际需要选择合适的N 值，图1为N=10 时的控制函数u(t)的曲线。

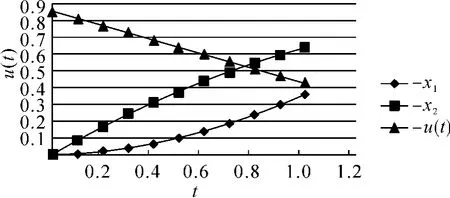
图1 控制函数u(t)的曲线

4 结论

笔者介绍了CMA 在求解动态优化问题中的应用，给出了详细的求解方法，并通过一个算例验证了方法的可行性。由于MA 及其改进算法CMA 是一种性能良好的智能算法，在实际应用中有广阔的应用前景，因此关于MA 及其改进算法的研究和应用还有大量的工作要做。

［1］ HOLLAND J H. Adaptation in natural and artificial systems［M］. Michigan: University of Michigan Press，1975:12－98.

［2］ CHANG T J，YANG S C，CHANG K J.Portfolio optimization problems in different risk measures using genetic algorithm［J］. Expert Systems with Applications，2009，36(7):10529－10537.

［3］ IP W H，HUANG M，YUNG K L，et al. Genetic algorithm solution for a risk－based partner selection problem in a virtual enterprise［J］. Computers ＆ Operations Research，2003，30(2):213－231.

［4］ WU Q H，CAO Y J，WEN J Y.Optimal reactive power dispatch using an adaptive genetic algorithm［J］. International Journal of Electrical Power Energy Systems，1998，20(8):563－569.

［5］ KENNEDY J，EBERHART R C.Particle swarm optimization［C］//IEEE International Conference on Neural Networks. Perth:［s.n.］，1995:1942－1948.

［6］ HAGAN M T，DEMUTH H B.Neural networks for control［C］//Proceedings of the 1999 American Control Conference.［S.l.］:［s.n.］，1999:1642－1656.

［7］ HOPFIELD J J.Neural networks and physical systems with emergent collective computational properties［C］//Proceedings of the National Academy of Sciences.［S.l.］:［s.n.］，1982:2554－2558.

［8］ ZHAO R Q，TANG W S. Monkey algorithm for global numerical optimization［J］. Journal of Uncertain Systems，2008，2(3):164－175.

［9］ 郝士鹏.混沌猴群算法及其应用［D］.天津:天津大学图书馆，2010.

［10］赵瑞清，郝士鹏. 一类新的模糊约束满足问题的建模与求解［J］.系统工程学报，2010，25(3):415－420.

［11］赵涛，夏雨，宗玛利.基于猴群算法的加气站项目进度研究［J］.价值工程，2010，29(8):90－92.

［12］张佳佳，张亚平，孙济洲.基于猴群算法的入侵检测技术［J］.计算机工程，2011，37(14):131－133.

［13］王靖然，余贻鑫，曾沅.离散猴群算法及其在输电网扩展规划中的应用［J］. 天津大学学报，2010，43(9):798－803.

［14］刘豹，唐万生. 现代控制理论［M］. 北京:机械工业出版社，2006:23－104.

［15］老大中.变分法基础［M］. 北京:国防工业出版社，2006:76－132.