显式Colebrook-White 摩阻系数方程

苑伟民

中国石化天然气分公司广西液化天然气工程项目部，广西 北海 536000

1 Colebrook-White 方程

在计算摩阻系数的众多方程中，Colebrook-White方程较为常用［1-3］：

式中： f 为为水力摩阻系数；ε 为为管道内壁粗糙度，m；D 为为管道内径，m；Re 为为雷诺数，无量纲量。

2 Colebrook-White 方程求解

隐式Colebrook-White 方程［4-6］，早期借助图表进行估算，误差较大；随着数值算法及编程软件的发展，可运用牛顿法、弦截法、抛物线法等迭代方法［7-9］或者使用数学软件进行求解［10-13］；但迭代法计算用时较长，应用数学软件有可能不能直接得出数值解。

2.1 Lambert W 格式的方程

使用MATLAB 求解式（1）得到如下最简形式：

Lambert W 函数定义为：W=Lambert W（x），表达的数学意义为：w*exp（w）=x。 LambertW 函数是一个超越方程的形式，不能直接应用于工程计算。

2.2 WrightOmega 格式的方程

使用Maple 软件求解式（1）得到如下最简形式：

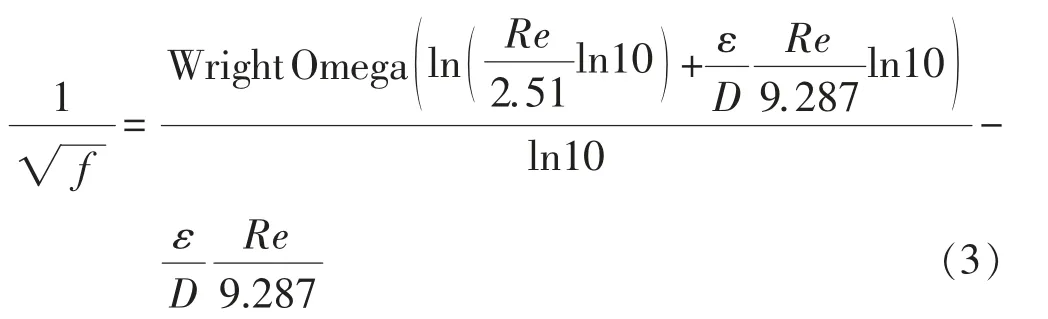
2.3 Product Log 格式的方程

使用Mathematica 软件求解式 （1） 得到带有Product Log 函数的方程， 形式更为复杂。 Product Log函数与Wright Omega 函数定义相同，仍然不能直接应用于工程计算。

3 Colebrook-White 显式方程

3.1 显式方程的推导

在数值方法研究的基础上，综合牛顿法和多重迭代法［7］，提出以下迭代法：

使用式（5）代替求导：

式（4）具有4 阶以上收敛阶。

3.2 显示方程的提出

将式（1）代入式（4），经过数学推导，简化得到显式Colebrook-White 方程：

4 计算实例

4.1 方程使用

4.1.1 已知参数

雷诺数Re=5 813 924， 粗糙度k=0.02 mm， 管径D=600 mm。

4.1.2 计算过程

将已知数值带入b、c、x0计算， 得到表1 数值，进一步带入式（6），即可解得摩阻系数。

4.2 结果分析

将式（6）与文献［10］中的方程（见表2）作对比见表3［10］。

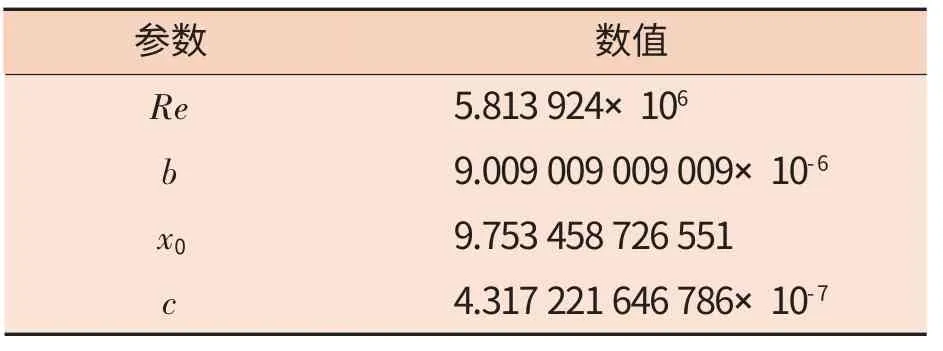
表1 数值表

表2 显式Colebrook-White方程［10］

表3 摩阻系数计算参数对比［10］

表3 中， 采用的精确值为1.050 336 403 193 8×10-2，该值是采用抛物线法和弦截法分别求解式（1）所得计算值的平均值。

生成100 组实验数据进行计算，式（6）计算结果的平均相对误差为（1.5×10-7）%，绝对误差为1.5×10-11；使用计算机编程求解， 计算所用时长约为抛物线法的1/32，约为弦截法的1/9。

5 结论

显式Colebrook-White 方程具有以下特点：

a）适用范围广，适用于所有雷诺数范围；

b）计算结果精度高，绝对误差数量级10-11；

c）计算时间短，远小于迭代算法；

d）形式简单，既适合手算也适合计算机计算。

［1］ Brown O G. The History of The Darcy-Weisbach Equation for Pipe Flow Resistance，In Environmental and Water Resources History［J］.ASCE Conference Proceedings 126 2002，126（4）：34-43.

［2］ Coelho M，Carlos Pinho. Considerations about Equations for Steady State Flow in Natural Gas Pipelines［J］.Braz.Soc.of Mech.Sci.&Eng.Vol.2007：XXIX，No.（3），262-273.

［3］［S.N.］［EB/OL］.http：//www.colebrookequation.com/，2008-05-06/2011-07-17.

［4］ Thomas G，Lester P E. Solving the Colebrook Equation for Friction Factors Part 1 of 3 in a Series of Articles［EB/OL］.http：//www.cheresources.com/colebrook1.shtml，2011-12-30/2012-01-05.

［5］ Thomas G，Lester P E. Solving the Colebrook Equation for Friction Factors Part 2 of 3 in a Series of Articles［EB/OL］.http：//www.cheresources.com/colebrook2.shtml，2011-12-30/2012-01-05.

［6］ Thomas G，Lester P E. Solving the Colebrook Equation for Friction Factors Part 3 of 3 in a Series of Articles［EB/OL］.http：//www.cheresources.com/colebrook3.shtml，2011-12-30/2012-01-05.

［7］ 钟尔杰， 黄延祝. 数值分析 ［M］. 北京： 高等教育出版社，2004：1-3.

［8］ 苑伟民，贺 三，袁宗明，等. 求解BWRS 方程中密度根的数值方法［J］. 天然气与石油，2009，27（1）：4-6.

［9］ 苑伟民，贺 三，袁宗明，等. 求解BWRS 方程中压缩因子的数值方法［J］. 管道技术与设备，2009，16（3）：14-16.

［10］ 苑伟民，青 青，袁宗明，等. Colebrook-White 方程显式公式对比研究［J］. 天然气与石油，2010，28（4）：5-7.

［11］ 苑伟民，贺 三，袁宗明，等.VB 与MATLAB 混合编程在求解天然气物性参数中的运用［J］. 中国科学论坛，2008，8（9）：21-23.

［12］［S.N.］.Colebrook Equation［EB/OL］.http：//www.engineeringtoolbox. com/colebrook -equation -d_1031.html，2011 -11-03/2011-08-05.

［13］ Wikipedia. org. Darcy Friction Factor formulae ［EB/OL］.http：//en.wikipedia.org/wiki/Colebrook -White_equation，2011-01-26/2011-07-05.

［14］ Corless R M，Jeffrey D J. Wright Omega Function［EB/OL］.http：//www.maplesoft.com/support/help/Maple/view.aspx?path=Wrightomega，2011-11-03/2011-08-06.

［15］ The Math works. Lambert W Function ［EB/OL］. http：//www.mathworks.com/help/toolbox/mupad/stdlib/wright.html，2011-11-03/2011-08-06.