干涉仪相位差测量精度及其影响因素分析＊

石 荣，阎 剑，张 聪

（电子信息控制国家重点实验室，四川 成都610036）

0 引言

干涉仪测向在频谱监管、电子侦察等领域应用广泛。大量文献对干涉仪测向的工作原理、设计准则、数据处理流程与使用方法等各个方面进行了全面的阐述［1-3］，部分文献还对干涉仪相位测量误差和测向精度问题进行了分析［4-5］，但是目前从普遍意义上来探讨干涉仪相位差测量精度与主要影响因素的并不多。本文主要针对干涉仪对单频电磁波测向应用中的通道间相位差测量精度问题展开讨论，建立了相关的数学模型，在频域对干涉仪相位差测量所能达到的精度进行了理论分析，讨论了影响测量精度的几个主要因素，并通过仿真对相关的分析结果进行了有效性验证，这对于干涉仪测向应用的分析论证与实际工程使用具有一定的参考意义。

1 干涉仪通道间相位差的测量方法

在单频平面电磁波条件下，设干涉仪的2个接收通道分别为A 与B，它们所接收到的信号分别为：

式中，t∈［0，ΔT］，ΔT 为测量时间，信号频率为f0，初始相位为φ，幅度为α，nA（t）与nB（t）分别是A 与B 两个接收通道引入的噪声与干扰，φ 为两通道接收信号的相位差，且：

式中，d 为两通道所对应的干涉仪两个接收天线之间的间距，λ为电磁波波长，θ为平面电磁波与天线视轴之间的夹角。由此可见，只要知道通道相位差φ 的测量精度，结合干涉仪基线参数与信号波长参数，就可以推导出干涉仪测向值θ所能达到的精度。

对于式（1）、（2），传统时域滤波求解过程是两式直接相乘，以及其中一个通道经过相移90°后两式相乘，2个乘积在低通滤波后可得到相位差的估计值，在不考虑噪声与干扰项的条件下可得：

式中，Filter＿LP（·）表示低通滤波算子。由上述两式可以直接求解出干涉仪两通道之间的相位差φ。但是在考虑噪声与干扰的条件下，通道间的乘积运算会因信号质量的下降而对测量精度产生影响，特别是在低信噪比条件下尤为突出。所以高精度的相位差测量都采用频域求解法。设式（1）、（2）所表示的信号在A／D采样后分别为：

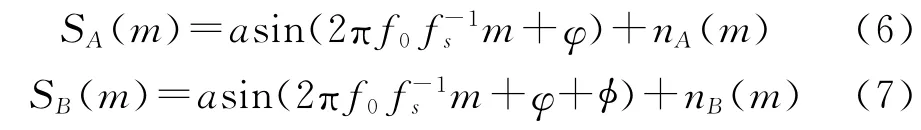
式中，m∈［1，N］，信号采样长度为N个点，采样频率为fs，且fsΔT 为N。对采样后的两通道信号分别进行DFT 离散傅里叶变换，即：

式中，k∈［1，N］，ωN为exp（-i2πN-1），并假设K0为，于是有下式成立：

式中，NA（k）和NB（k）分别是通道噪声与干扰nA（m）和nB（m）的DTF序列。由上可见，在频域内通过被测信号所在频点处对应的相位值，可直接得到通道相位φ 与φ＋φ的估计值，进而求得通道相位差（φ＋φ）-φ的估计值＾φ。为理论推导的简洁性，避免DFT 过程中单频信号在频域出现频谱泄漏现象，上述分析过程中实际隐含着KD为整数的假设。在实际应用中，也可以通过补零DFT 等方法，增大DFT 运算点数以避免频域的频谱泄漏。这同样可以在信号所在频率点处获得通道相位的估计值，且不影响整个理论模型的有效性。

2 相位差测量精度的理论模型与影响因素

2.1 信号空间模型与测量精度分析

前一小节直接从频域来估计通道中信号的相位值，在测量持续时间内的单频信号变换到频域，将会把信号能量集中在一个频率点上，其频域幅值记为X。如果在矢量信号空间中来分析这一问题，实际上可以描述为一个信号矢量X 和一个噪声与干扰矢量N 叠加合成一个综合矢量Y，相位测量值＾φ 是综合矢量X对应的相位值，而真实的相位值φ 是信号矢量X 对应的相位值，记相位估计误差Δφ 为＾φ-φ，Δφ∈（-π，π］，整个信号空间矢量叠加与相位求解如图1所示。

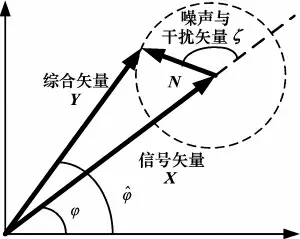
图1 频域信号矢量叠加与相位求解关系示意图

设被测信号所在频点上的噪声与干扰矢量N 的幅度为V，相位为ζ，其二维概率密度分布为pdf（V，ζ）。这一个概率密度分布函数与干涉仪接收通道噪声的概率分布有关，也与接收通道受到的干扰有关，不同的噪声与干扰对应着不同的二维概率密度分布，难以唯一地进行显式描述，但在实际应用中可以针对具体的干涉仪对象在不同频率点处实际测量得到，所以后续可将pdf（V，ζ）作为一个已知参量来对待。

在Δφ 不为0，π的条件下，根据平面几何的正弦定理，有下式成立：

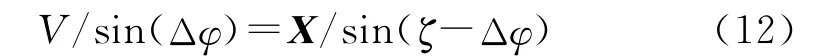
于是可得相位值Δφ 与ζ 的二维联合概率密度函数如下：

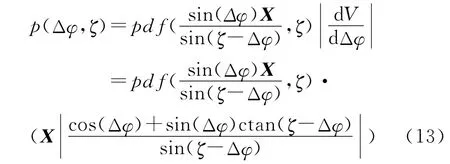
将上述二维概率密度分布转换成相位估计误差Δφ 的一维概率密度分布f（Δφ）如下：

在求得干涉仪每一个通道接收信号的相位值估计值之后，通过相减运算可直接得到干涉仪A 与B 两通道间的相位差估计值＾φ，其测量精度可用方差来描述，如式（15）所示：

式中，fA（Δφ）和fB（Δφ）分别表示通道A 和B 的相位估计误差的概率分布函数。

2.2 主要影响因素分析

从上面建立的干涉仪相位差测量精度理论模型可知，直接从数学方程上看，影响测量精度的参数有2个，分别是：频域中噪声与干扰矢量N 的概率分布函数，频域中信号矢量X 的幅度｜X｜与噪声干扰矢量N幅度V 的相对比值。

对于噪声与干扰矢量N 的概率分布函数pdf（V，ζ）来说，其中的相位因素ζ，在［0，2π）范围内一般服从均匀分布，而幅度因素V 的概率密度分布为：

1）瑞利分布

2）广义瑞利分布或莱斯分布

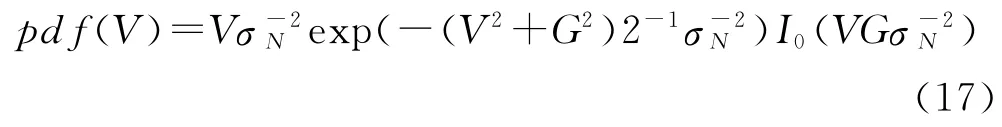
式中，I0（·）表示零阶修正贝塞尔函数，G 表示该频率点上干扰的频域幅度。该类分布一般在该频率点的干扰为单音干扰，并且通道噪声满足AWGN 加性高斯白噪声模型条件下成立。其中的单音干扰一般是由于变频杂散、本振泄露等因素造成的，在宽带干涉仪中比较常见。

3）对于其它类型的噪声与干扰矢量幅度V 的概率密度分布，可以通过实测数据获得。

根据DFT 的定义与性质，对于频域中信号矢量X的幅度｜X｜与噪声干扰矢量N 幅度V 的标准差的相对比值，可由如下2个因素来综合描述：信号的综合载噪比C／nz和测量持续时间ΔT，其中C 表示信号的功率，nz表示单位赫兹内噪声与干扰分量的功率。由于综合考虑了噪声与干扰两方面的因素，所以此处用综合载噪比来表示，且有下式成立：

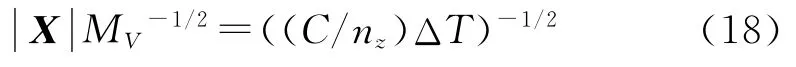
式中，MV表示V 的二阶原点矩，即MV为（V，ζ）dVdζ。由前面的信号空间矢量分析图可知，增加信号的综合载噪比C／nz与测量持续时间ΔT，可以减少估计误差的方差，从而提高干涉仪通道间相位差测量的精度。

综上所述，干涉仪相位差测量精度的主要影响因素是：频域中噪声与干扰的概率分布函数，综合载噪比和测量持续时间。实际上上述3个因素的相互作用是比较复杂的，主要是因为工程实际应用中干涉仪通道中噪声与干扰的概率分布繁杂，直接用显式的数学表达式来描述比较困难，但是另一方面也可以通过实际测量数据来获得干涉仪通道中噪声与干扰的概率分布函数，从而通过式（15）来对该干涉仪在不同条件下的通道相位差测量精度进行分析与评估。

2.3 仅考虑AWGN 条件下的精度分析结果

前面论述了影响干涉仪相位差测量精度的3个主要因素，其中最复杂的因素是噪声与干扰的概率分布函数，不同的分布函数将导致不同的测量精度。其中最简单的一种概率分布函数就是仅考虑AWGN 加性高斯白噪声，此时矢量N 的相位服从均匀分布，幅度服从瑞利分布，且有MV为2σ2N。假设干涉仪2个通道之间具有良好的一致性，即噪声的概率分布特性是一样的，下面以几种典型情况为例来加以说明：

1）（C／nzΔT）1／2≫1的情况。从平均意义上说，此时频域中信号矢量幅度远大于噪声矢量幅度。

2）（C／nzΔT）1／2大约为2～3时的临界情况。从平均意义上说，此时频域中信号矢量幅度大约是噪声矢量幅度的2～3倍，按照高斯分布特性2、3倍标准差内的幅度值出现的概率分别为：95.45%、99.73%，以此为门限做检测与相位差测量是临界情况。

如果（C／nzΔT）1／2低于临界条件，则在频域进行信号检测较困难，在此基础上实施干涉仪测向就更加困难了，所以干涉仪测向应用一般在临界条件以上使用。综上所述，在（C／nzΔT）1／2不同取值情况下，通过式（14）计算出的相位估计误差的概率密度f（Δφ）如图2所示。

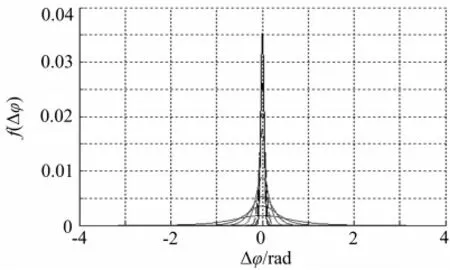
图2 在（C／nzΔT）1／2不同取值情况下Δφ 的概率密度分布图

图2中的7条曲线分别是（C／nzΔT）1／2为1，2，3，5，10，15，20时的曲线。利用上述概率密度分布函数，通过式（15）便可计算出干涉仪通道间相位差测量误差＾φ的标准差与（C／nzΔT）1／2之间的关系如图3所示。

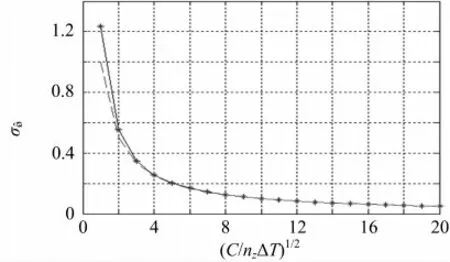
图3 σφ＾与（C／nzΔT）1／2的关系曲线图

3 仿真分析

前面对干涉仪相位差测量精度的理论模型与主要影响因素进行了分析，下面针对不同条件通过蒙特卡罗仿真对上述理论推导得出的结果进行验证。

仿真条件为：采样率1GHz，信号测量时间长度取为1μs，对应1000个采样点。单频信号的载波频率为125MHz，干涉仪两个通道之间接收到的信号之间的相位差为0.6π，干涉仪接收通道中没有干扰分量，仅存在AWGN 噪声分量。（C／nzΔT）1／2分别取1～20时，通过蒙特卡罗仿真，可得到相位差测量误差的标准差，将其绘制成曲线如图4所示。

图4 通过蒙特卡罗仿真得到的与（C／nzΔT）1／2的关系曲线图

图4中线型为虚线的曲线为反比参考曲线，实线曲线为仿真结果曲线。当C／nzΔT≥4时，标准差σφ＾与（C／nzΔT）1／2之间近似成反比关系；当C／nzΔT≤3时，二者之间的反比关系不再成立，相位差测量误差迅速增大。通过图4与图3的对比可见，蒙特卡罗仿真得到的结果与前面理论推导的结果具有高度的一致性，这同时说明了前面理论模型的有效性。

4 结束语

本文针对干涉仪对单频电磁波测向应用中接收通道间相位差测量的精度问题进行了理论分析，讨论了影响测量精度的几个主要因素，包括：信号综合载噪比、测量时间、频域噪声与干扰的分布特性等。所得到的仿真结果与理论计算结果具有高度的一致性，从而验证了理论分析的有效性。这样在实际应用中，可直接利用上述理论分析得到的精度曲线，开展对干涉仪测向的系统设计，测量误差分析等设计论证工作，所以本文的分析结果对于干涉仪测向的实际工程应用具有一定的参考意义。■

［1］王金辉.相位干涉仪测向系统算法研究［J］.电子质量，2010（3）：14-16.

［2］李银波，陈华俊.鉴相方法的分析与比较［J］.电讯技术，2008，48（6）：78-81.

［3］胡宗恺，饶志宏.高精度数字鉴相技术的FPGA 实现［J］.通信技术，2010，43（12）：177-179.

［4］田德明.影响干涉仪测向接收机测向精度的因素分析［J］.舰船电子对抗，2010，33（2）：45-48.

［5］王国华，李长满，许剑锋.数字化宽带测向系统中的相位差测量及误差分析［J］.电子技术，2009（1）：61-64.