基于RBF神经网络模型的电站锅炉燃烧优化
2013-12-20鲍春来张竞飞
鲍春来,张竞飞
(华北电力大学 能源动力与机械工程学院,保定071003)
电站锅炉是火力电站的主要设备,其运行的性能直接影响火电站的经济指标和环保指标。笔者以火电厂锅炉燃烧过程为研究对象,在引入人工神经网络之RBF网络的基础上,建立了锅炉的运行优化模型。建立的神经网络模型以与电厂燃烧控制系统有密切联系的机组负荷、一次风量、二次风量、燃尽风量等作为输入变量,以二次风挡板开度等作为输出变量,用电厂采集到的历史数据样本进行训练,由此得到优化模型。
1 RBF神经网络
RBF神经网络是一种局部性神经网络模型,其网络模型见图1。它的生物基础是存在于大脑皮层和视觉皮层的局部调节与交叉重叠的接受域,因此这种采用局部接受域来实现函数映射的神经网络结构和基于插值与近似理论的网络结构被统一称作径向基函数神经网络[1]。
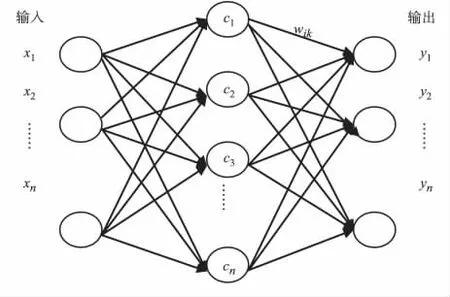
图1 RBF神经网络结构图
网络学习的过程就是对各个参数调整、修正、完善的过程,本文采用的是一种最临近聚类的算法,将存在于中心内一定范围的点都汇聚到中心,并按均值修正中心的位置;同时为了避免初期训练时中心点的频移过大,所以采用了改进的“加权聚类法”来减小距离中心较远点对中心的影响。
RBF神经网络的训练算法如下:
设有q组训练样本,输入的X=(x1,…,xn)是一个n维向量,T=(t1,…,tn)是输出的m 维向量,所以是一个n×m的网络。该网络初始的隐含层节点只有一个。()作为样本,C1=()是隐含层第一个节点中心,隐含层的输入输出之间权值大小w,w1j=定义节点中心宽度、聚类距离、网络最大的允许误差和修正步长分别为σ,d,emax,μ。
取第p(2≤p≤n)组样本,设此时的网络中有h个隐含层节点,则进行图2中流程的运算。若所有的样本都己训练完,则训练运算结束;否则取下一组样本,继续进行上述过程的学习。

图2 算法训练过程图
当样本训练完成后应该使用全部样本再训练一遍网络,同时按全局最优修正权值,以最终确定网络[2]。
2 影响锅炉燃烧的因素
针对某电厂采用前后墙对冲燃烧的锅炉,其燃烧效率和NOx的排放质量浓度与过量空气系数、燃烧器的结构参数、燃尽风量、磨煤机投运组合方式及煤质变化有较大关系,其中NOx排放质量浓度主要受过量空气系数、燃尽风量、磨煤机的投运组合方式和煤质变化的影响 ,而燃烧器结构的变化对其影响较小[3]。
具体分析如下:
(1)过量空气系数增大时NOx的排放质量浓度随之增加,过量空气系数减小时锅炉热效率逐渐提高;但为了控制水冷壁的高温腐蚀和炉膛结渣,锅炉的过量空气系数应在一个合理范围内。
(2)燃尽风量增加时,炉膛内烟气中的氧气体积分数降低,CO的体积分数增加,这样会明显降低NOx的生成量。燃尽风率在刚开始增加时飞灰中碳的质量分数是有所降低的;但当燃尽风率增加到一定程度之后,炉膛出口飞灰中碳的质量分数随燃尽风率的增大而升高,使锅炉的不完全燃烧热损失随之增大。
(3)磨煤机的投运组合方式也就是燃烧器层投运方式,其组合方式的不同会导致主燃烧区和燃尽风(OFA)区域的距离发生改变,从而使NOx的排放质量浓度受到影响。如将最上面燃烧器停用时,则NOx的排放质量浓度最低;若将最下面的燃烧器停用时,则NOx的排放质量浓度最高。
(4)煤种影响,其NOx的排放质量浓度会随着煤的含氮质量分数和挥发分质量分数的增加而降低。
(5)一次风量的增减对制粉系统的运行影响较大,小幅度增加一次风速即可能降低锅炉效率,但对NOx的排放质量浓度影响不大。二次风门全开时锅炉效率比二次风门全关时略高,但其NOx的排放质量浓度却比全关时增加明显。
3 燃烧优化模型的建立
3.1 确立燃烧优化目标函数
600MW机组燃煤锅炉的优化目标函数为:

式中:A、B分别是影响NOx排放、锅炉效率的参数集合;m(NOx)为 NOx的排放质量浓度;ηgl为锅炉效率。
寻优的目标即为X越小越好,因此从运行历史数据中找到多个能满足寻优目标的参数集合,首先是找到影响NOx排放质量浓度和锅炉效率的因素集。
锅炉运行性能参数决定着燃烧状况,当某一性能参数超出规定范围时,需要通过相应的调整使性能参数回归于规定范围,因此需要找出使性能参数发生变化的可调量,以便当性能参数超出规定范围时可迅速调节这些可调量。将调节系统看成一个子组,则对一个子组的可调量进行调整会引发那些状态量和性能参数变化。找出调节量对应的性能参数的变化,就可对应地找出使某一性能参数变化的最直接调节量。
3.2 优化目标的确定
锅炉燃烧过程中参变量的数量和种类都非常多,可以选择的优化目标也很多。由于建立神经网络的目的是用以进行优化指导,所以优化目标包括在模型输出的参量之中;同时根据不同的需要,可以在输出参量中灵活地选择优化目标;对于多目标优化问题,还可将多个优化目标按照一定原则组合在一起。本文从经济性和环保性角度出发,选取影响锅炉热效率与锅炉NOx排放质量浓度组成优化目标。
当这两个量同时作为优化目标的时候,同时实现优化有一定的难度,所以就必须将两个优化目标能够变成单目标的问题。最常用的合成方法就是通过加权平均、乘除法以及功效系数法等。考虑到本文优化对象的输入与输出都不是单个的量,而优化算法是针对单个目标的,所以采用线性加权合法来作为目标的统一方法:

式中:m为目标的个数,分别给各单一的目标函数分配上权系数λi,将其作为新的目标函数[4]。
3.3 输入和输出参数的确定
影响燃烧特性的主要因素大体可总结为:负荷、燃煤特性、二次风与燃尽风配风方式、过量空气系数、一次风粉质量浓度沿高度方向的分布等。本文选择较为重要的运行状态参数作为燃烧优化的输入量:(1)总风量与入炉总煤量代表负荷对燃烧效果的影响;(2)选择5个给煤机开度及5台磨煤机通风量作为输入参数;(3)二次风前后墙各投放3层,共6层,取6个二次风门开度作为影响因素,用以描述二次风对燃烧优化状态的影响;(4)取风箱与炉膛压差作为一个输入参数;(5)有2层燃尽风,取2层燃尽风开度值作为描述燃尽风影响的输入参数;(6)空气预热器中空气温度值也是影响因素之一;(7)采用省煤器后的烟气中氧气的体积分数作为氧量对燃烧的影响因素;(8)煤种特性取电厂每天定时化验的全水分、空干基水分、干燥基灰分、干燥无灰基挥发分和收到基低位热值作为输入参数。
将测试所得数据作为输入参数值,将锅炉效率和NOx排放质量浓度作为求取的输出参数值。
3.4 锅炉燃烧(高效低NOx)优化系统实现
锅炉负荷和燃用煤种对某特定工况是不可调的,锅炉运行人员可以根据优化目标的不同,调整各个可调参数的具体数值。由于在优化计算时存在约束条件(例如一、二次风压),所以必须保证在锅炉安全运行的范围内进行调整,不可因优化目标而影响安全生产。
本文实例中需要优化的可调输入参数为二次风挡板开度、燃尽风门开度和烟气中氧气体积分数;输出参数为锅炉热效率、NOx排放质量浓度。神经网络模型优化结构见图3。
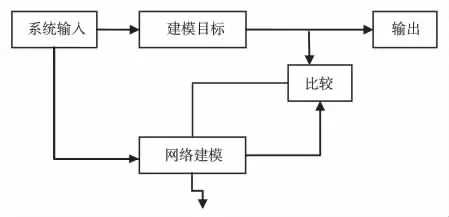
图3 神经网络模型优化图
4 算例与求解
4.1 低NOx排放的优化
参照上文中描述的优化问题所采用的数学模型进行参数设置,从采集到的用于训练的神经网络的数据样本中选择出NOx排放质量浓度(m(NOx))最高、最严重的工况组进行优化计算,式(2)中取λ1=1,λ2=0,在负荷一定的情况下单纯进行NOx优化实验。将训练好的神经网络作为求取目标值的目标函数,通过优化算法获得额定负荷下的NOx质量浓度最低时的二次风门和燃尽风门的开度值(只取其中的最优值,不采用次优解)。
通过多次的迭代求得各个优化参数最优值,输入值见表1,输出值见表2。
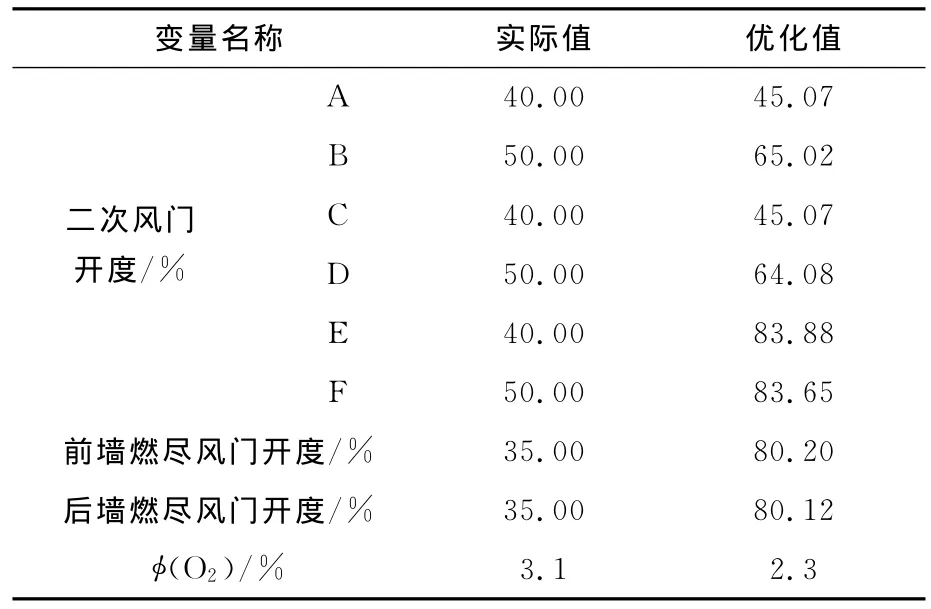
表1 以低NOx排放为目标的优化参数输入值
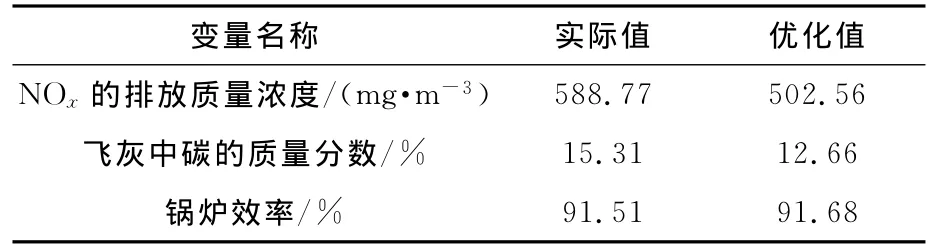
表2 优化输出值
优化结果表明:采用较大开度的燃尽风开度对于降低NOx的排放质量浓度有利,优化后的风门开度意味着炉内燃煤量与空气的比例状况得到调整,从而达到NOx质量浓度的降低;模型提供的优化建议也与抑制燃料型NOx生成的原则相一致。由于优化目标采用的是单一量,所以锅炉效率变化并不大。
4.2 锅炉效率优化
取λ1=0,λ2=1,在负荷一定的情况下单纯进行锅炉效率优化实验,其结果见表3及表4。
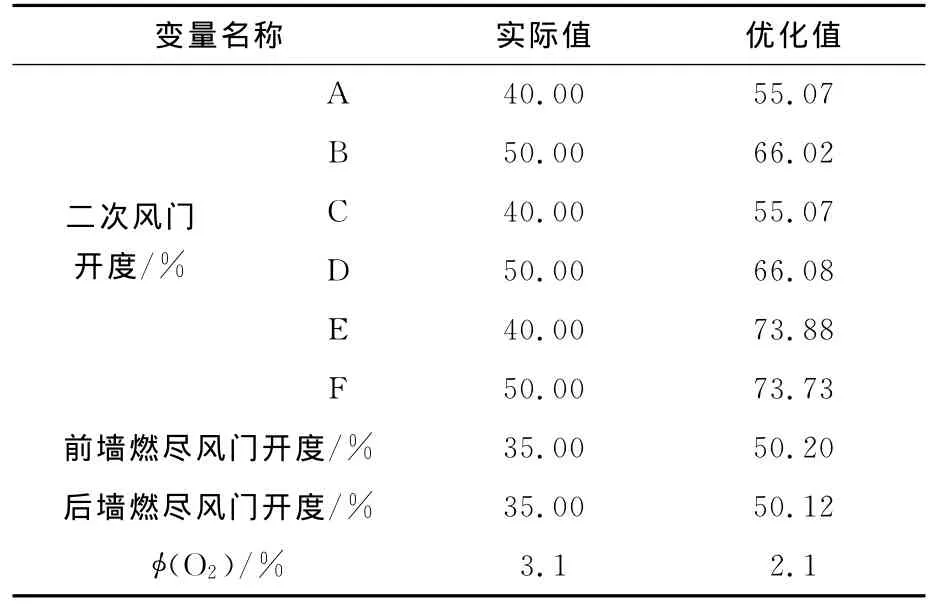
表3 以高锅炉效率优化目标的输入值

表4 优化输出值
4.3 锅炉效率与m(NOx)同时优化
取λ1=0.5,λ2=0.5,当两个优化目标的权重大小相同时,得到两方面都兼顾的优化目标,其结果见表5及表6。
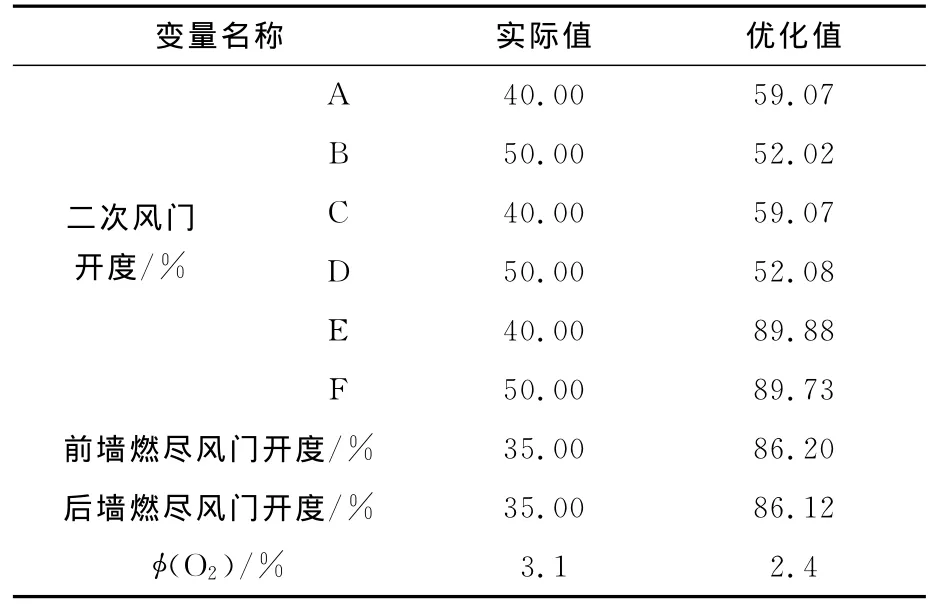
表5 两者兼顾的优化结果输入值
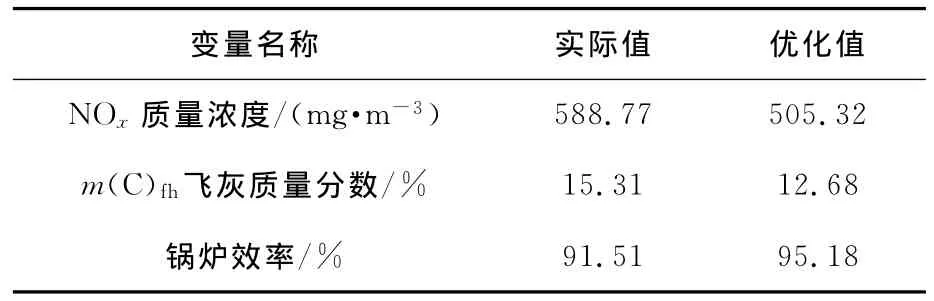
表6 优化输出值
4.4 存在的不足
由于飞灰中碳的质量分数m(NOx)的测量值并不准确,m(NOx)也需要更精确的值,锅炉效率也受到排烟温度和飞灰中m(C)fh的影响,所以优化的结果并不完全满意,需要进一步研究和改进。
5 结语
本课题以某电厂锅炉为研究对象,利用RBF神经网络的手段,建立了锅炉在复杂燃煤情况下的燃烧模型,在建立的神经网络模型的基础上取出当输出目标为最佳值时的各个可操控变量的设定参考值,将这些参考值提供给锅炉的调节机构,进而达到锅炉优化运行的目的。
结果表明:根据模型建议的燃烧参数调整,可准确改善锅炉运行情况,明显降低NOx排放质量浓度,提高锅炉效率,具有一定的实用价值。
[1]陈磊 .神经网络在电站锅炉燃烧优化中的应用研究[D].长沙:长沙理工大学,2009.
[2]潘维加.300MW单元机组煤粉炉燃烧控制系统的研究及其改进[J].中国电机工程学报,2000,20(9):78-80.
[3]周思远,黄孝彬,闫顺林 .针对600MW前后墙对冲燃烧优化模型的确立与分析[J].应用能源技术,2011(10):23-25.
[4]许力 .智能控制与智能系统[M].北京:机械工业出版社,2007:207-210.
