UTM投影和Gauss-Krüger投影及其变换实现

2013-12-19周朝宪房志峰于彩虹张云国高应波燕丹晨

地质与勘探 2013年5期

周朝宪，房志峰，于彩虹，张云国，高应波，燕丹晨，杨强

(1.有色金属矿产地质调查中心，北京 100012;2.中色地科矿产勘查股份有限公司，北京 100012;3.北京矿产地质研究院，北京 100012;4.山东政法学院信息科学系，山东济南 250014;5.中国科学院遥感应用研究所，北京 100101;6.国家海洋环境预报中心，北京 100081)

1 引言

所谓投影，包括2部分内容，一是对地球这个椭球体参数最佳近似的理论化;二是把这个理论化的地球椭球体上的坐标点(大地坐标系的经纬度)转到(主要通过解析变换、数值变换和数值解析变换)(杨启和，1986;吕晓华等，2002;夏兰芳等，2007)平面坐标(即方里网)上。投影变换对于航天、航空、航海、建筑、军事和地质起着至关重要的作用，现实生活也一刻离不开投影变换。几百年来，人们发明了各种投影算法，如面投影、线投影和角度投影(杨启和，1981，1994a，1994b;Snyder，1987)等，但是各种投影都有其优点也都有其缺点。无法保证角度、方向、长度和面积等同时不失真，只能顾及一部分而尽力抑制其他部分的失真。如Gerarus Mercator于1569年提出了墨卡托(Mercator)投影，尽管其投影后的长度和面积都失真，并且从赤道到两极畸变越来越大，但是保证了在投影后任意一点上的角度和形状不失真，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对飞行器和船舰在航行中的定位、确定航向都具有有利条件，给航行者带来很大方便。墨卡托投影图很利于导航，省去了大量畸变矫正计算。

在此基础上，人们逐渐发展出横墨卡托(Transverse Mercator，即TM)投影，TM投影的一个发展方向是正切的 Gauss-Krüger(高斯－克吕格)投影，为前苏联、中国和德国等所采用，随后又发展出另一种投影，即横正轴割UTM(Universal Transverse Mercator，通用横墨卡托)投影，现在为大部分国家所采用。尤其随着地勘行业“走出去”的实施和加快，我们必须熟悉国外通用UTM坐标。另外，GPS系统也越来越广泛地使用于国内建设，如国内近些年开始广泛使用的GPS接收机，再者，对任一点的大地经纬度坐标和Gauss-Krüger投影之间的转换比较麻烦，尤其是到一个新区工作。而对任一点的大地经纬度坐标和UTM坐标之间转换相比十分简便，不需要各个地区的特定校正参数。UTM投影替代Gauss-Krüger投影已成大势所趋(沈本忠，1986;Li et al.，2003)。另外，我国的卫星数据一般采用UTM投影。这些都对我们熟悉和掌握UTM坐标提出了迫切要求，要求我们了解UTM投影，掌握其和大地坐标以及Gauss-Krüger投影坐标之间的相互转换。但是，现在的国内教科书，如2006年版的《控制测量学》(孔祥元等，2006)，也往往对UTM投影介绍得远不如Gauss-Krüger投影详细。另外，我们国内在对UTM投影和Gauss-Krüger投影原理的理解上往往有些偏差，在投影变换使用上还有些差距。本文在此试图对此进行简单探讨。

2 Gauss-Krüger投影

无论Gauss-Krüger投影还是UTM投影都是TM投影，TM投影不是球心透视横圆柱投影(王正梅等，2002)①，在百度百科②上也把Mercator错误解释成球心透视横圆柱投影。因为前者是等角度投影，而后者是任意投影，不能保证其等角度。

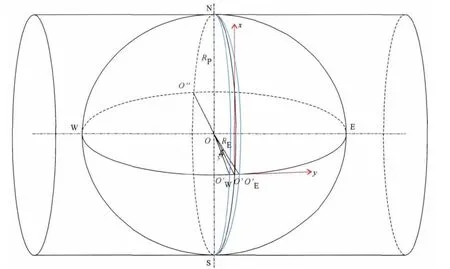
图1 Gauss-Krüger投影Fig.1 Gauss-Krüger projection

无论是UTM投影还是Gauss-Krüger投影都是等角投影(又称正形投影)，即投影后的任意一点上长度与方向无关，依然保持投影后该点的微小图形相似性。

Gauss-Krüger投影由 C.F.Gauss在进行汉诺威地区的测量中提出(使用双投影，即从椭球体投影到球体，然后投影到平面)，并由J.H.Krüger于1912年对其进行了改正，采用单一等积投影(A single equivalent projection)，并做了进一步数学推导而完成。Gauss-Krüger投影为椭圆柱横轴正切地球椭球体，椭圆柱的中心通过椭球体。从而将椭球体上的点投影到椭圆柱上。正切线为中央经线，将中央经线两侧各3度(即6度带投影)和1.5度(即3度带投影)作为一个投影带进行投影。见图1。

由此，Gauss-Krüger投影条件如下(杨启和，1981;王正梅，2002;孔祥元等，2006):

(1)中央经线和赤道投影为互相垂直的直线，并为其他经纬线的对称轴，离开赤道的纬线是弧线，凸向赤道。离开中央经线的其他经线是弧形，凹向中央经线。离开中央经线越远，变形越大。

(2)投影后无角度变形，即正形投影。

(3)中央经线投影后无长度变形，即中央经线圆为标准经线圆(standard line)。

据此可知其数学公式。其数学公式在很多文献中都有论述，如杨启和(1981)、孔祥元等(2006)、Deakin et al.(2010)、Kawase(2011)和 Dorrer(2003)，故不在此叙述。

3 UTM投影

UTM投影为美国陆军工程兵测绘局(Army Map Service，US Army Corps of Engineers)于 20 世纪 40年代提出(Langley，1998)。当时对美国本土采用Clarke 1866椭球体，对全球其它地方，包括夏威夷，采用国际椭球体(International Ellipsoid)。韩国建等(1994)所说的UTM采用Clarke 1866椭球体是不严谨的。UTM投影现在采用WGS(World Geodetic System)84椭球体(其最新版为2004年修订的EGM(Earth Gravitational Model)96③。

UTM投影为椭圆柱横正轴割地球椭球体，椭圆柱的中心线位于椭球体赤道面上，且通过椭球体质点，从而将椭球体上的点投影到椭圆柱上。两条割线圆在UTM投影图上长度不变，即2条标准经线圆。两条割线圆之正中间为中央经线圆，中央经线投影后的长度为其投影前的0.999 6倍，比例因子k=投影后的长度/投影前的实际长度。则标准割线和中央经线的经度差为 1.620 6°，即 1°37'14.244″。参见图2。具体推导为:

中央经线投影的比例因子k=0.999 6，即为中央经线圆(通过地球椭球体质点O、南北极N和S以及O'C的圆)圆周长的0.999 6倍为其同心圆(即弧段 N标O—O'T—S标O，圆心为地球椭球体质点 O，叫做中央标准圆，即图2中圆心为O点的红色圆)圆周长。这样N标O—O的长度(表示为N标OO，下同，略)=地球极半径RP(即NO)的0.999 6倍。N标OO=N标EO标E(O标E为线 N标ES标E和线 WE 的交点)，则:

sin(α)=N标EO标E/R标=N标OO/R标=0.999 6 ×RP/R标

式中α为角N标E—O－E，即点N标E的纬度。R标为标准割线圆上(也在地球椭球体表面上)N标E的地球椭球体半径。

由于纬度很高，接近90°，故可做近似RP=R标，则

sin(α)=0.999 6 ×RP/R标=0.999 6，则

α =88.379 4°

可以算出横正轴割椭圆柱与地球椭球体割线的纬度为 88.379 4°N 和88.3794°S(如图2)。而一些学者，如韩国建等(1994)、孙立东(2008)、陈悟天(2010)、刘明波等(2010)和熊忠招(2010)等认为，椭圆柱割地球于80°S和84°N。从我们的计算来看，他们的此种观点是错误的。退一步讲，如果他们的观点是对的，则正轴割的条件不能成立，即椭圆柱中心线不在椭球体赤道面上并通过椭球体质点。何况这样的话，也不符合UTM的投影条件。

这样，可以求出两个标准割圆和中央经线圆之间的距离 N标ON标E为:

N标ON标E=RE×sin(90°－88.3794°)=RP×sin(90°－88.3794°)=179 776 m。

式中，极半径 RP=6 356 752.314 245 m(根据WGS 84地球椭球体参数③)。

即标准割线圆在UTM投影上距离中央经线距离为179.776 km(见图3)。这样，陈悟天(2010)所说在UTM投影带中央经线两侧330 km处各有一个标准经线是错误的。

每个UTM投影带为经度6°。对一个窄经度(如6°)带投影而言，Gauss-Krüger投影以其中央经线保持长度不变，而向中央经线两侧逐渐变形，明显不如UTM保持中央经线缩短至0.999 6，而出现2条长度不变的子午线的整个投影带上的长度变形合理，改善了该6°带内长度投影变形分布(图3)。这也是UTM投影相比Gauss-Krüger投影的长处之一。

由此，UTM投影除了中央经线投影后长度缩短0.0004，其两侧的两条割线的长度无变化外，和Gauss-Krüger投影条件基本一样(杨启和，1981;王正梅;2002;孔祥元等，2006;)。其数学推导公式在很多文献中都有论述，如，Dozier(1980)、Osborne(2008)和 Deakin et al.(2010)。故亦不在此叙述。

从赤道随着纬度的增加，收敛角(即真北和UTM投影北的夹角)越来越大。为保证投影的精度及大陆地区投影的一致性，UTM投影仅适用于纬度84°N和80°S的范围(这个范围覆盖了除南极洲外的几乎所有陆地)。

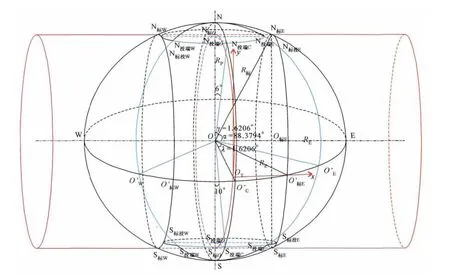
图2 UTM投影Fig.2 UTM projection

4 UTM投影和Gauss-Krüger投影异同

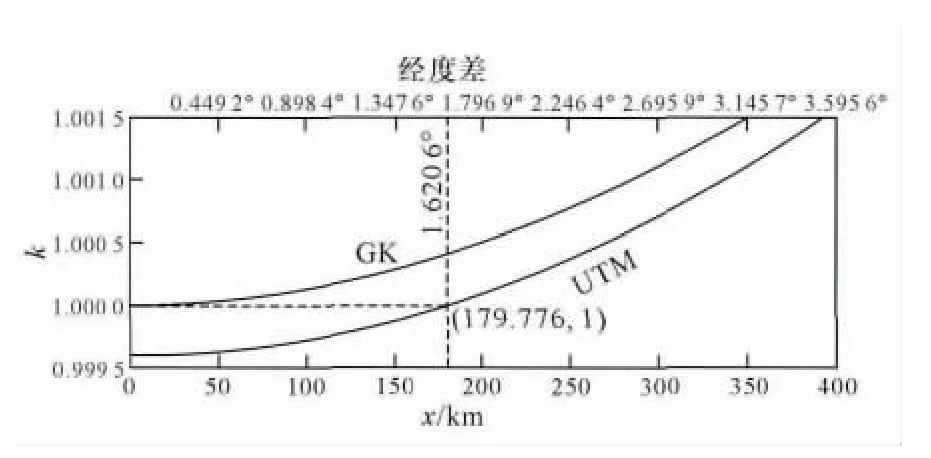
图3 经线圈长度投影变形因子k随该经线圈与中央经线的距离x的变化Fig.3 Variation of k with the distance x from the central meridian

4.1 Gauss-Krüger投影分带和UTM投影分带及其带号

二者同属TM投影，其根本性的区别在于其数学公式的区别。我们在此仅仅讨论应用中二者的差异，以利于工程使用。以前国内说的3度带和6度带是指Gauss-Krüger投影而言，6度带起始经度0°，即0～6°E为6度带带号为1，沿着赤道经线一次向东类推，带号也一次增加。3度带起始经度为1.5°E，即1.5 ～4.5°E 为3 度带，带号为1，以此类推，共120带。

UTM分带的起始经度为180°W。即180°W～174°W，其带号为1，依次向东逐个累加。和Gauss-Krüger 6度带投影一样，也是全球共分60个6度带。

4.2 Gauss-Krüger投影和 UTM 投影伪偏移

两种投影的东伪偏移都是 500 km，Gauss-Krüger投影北伪偏移为零，UTM北半球投影北伪偏移为零，南半球则为10，000 km(见图4)。

图4 一个UTM投影6度带(据Langley(1998)修改)Fig.4 An UTM projection 6 degree zone(modified from Langle，1998)

4.3 Gauss-Krüger投影和UTM投影x和y坐标

UTM投影与Gauss-Krüger投影的x和y坐标是相反的，即UTM投影中x和y分别为经向和纬向数值(图2和图4)，而Gauss-Krüger投影中x和y分别为纬向和经向数值(图1)。具体原因源自于其投影数学公式，亦可参见图1、图2和图4。

5 投影变换实现

UTM投影与Gauss-Krüger投影相比，中央经线的长度比为0.999 6，严格的数学换算比较复杂，手工计算基本是不能实现的，常借助于软件来实现。有人提出了简易的算法公式，但是因为简易公式得出的结果是，这两种投影数学公式的差异差别300 m。这在实际工作中是不可以接受的。

我们国内常用的MapGIS软件没有UTM投影，且不怎么适用于国外的经纬度，如没有南半球纬度。ArcInfo软件无国内现用的Gauss-Krüger投影。相比之下，MapInfo®(2010 Pitney Bowes Software Inc.)兼有包括UTM投影和Gauss-Krüger投影在内的众多投影，且市场占有率较大，易于获得。故此本文采用MapInfo® Professional版本10.5来探讨一下如何快速实现批量投影变换，其步骤如下:

(1)将数据输入或者转成Excel文件(如文件名字为“坐标变换.xls”)，使用 MapInfo®打开“坐标变换.xls”文件。生成“坐标变换.TAB”，关闭MapInfo®。然后重新打开“坐标变换.TAB”文件。点击“表－创建点(Create Points)”，确认投影为“Longitude/Latitude(WGS 84)”(这里先以经纬度为例转成UTM方里网过程为例简要描述)，并设置x和y相对应的经纬度坐标列，设置生成点的样式，生成点对象，并将生成的点对象另存为“坐标变换A.TAB”文件。然后关掉MapInfo®。

此时注意确认投影(Projection)椭球体，如UTM投影采用WGS 84椭球体(图5)，并进一步指出投影所属的带号和南北半球。有些地图的经纬度使用的不是WGS 84椭球体。遇到此种情况，在图5的“投影”(Projection)中选区正确的投影椭球体。如非洲有些国家的地图使用Arc 1960体系，则图5中应该选择“Longitude/Latitude(Arc 1960)”，如不加以改正，将相对于选择“Longitude/Latitude(WGS 84)”椭球体将产生数值向NNW偏移281 m。

(2)重新打开“坐标变换 A.TAB”文件，点击“表－更新列(Update Column)”，使用对话框(如图6)对UTM投影x和y坐标列分别进行更新，得到UTM投影的方里网x和y坐标(图7)。可以导出所得坐标。

对方里网坐标转成经纬度坐标步骤基本同上，只是在上述第二步“创建点”时采用UTM投影或Gauss-Krüger投影，第三步“更新列”时采用经纬度投影。

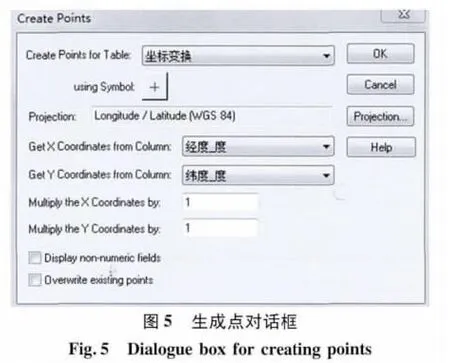
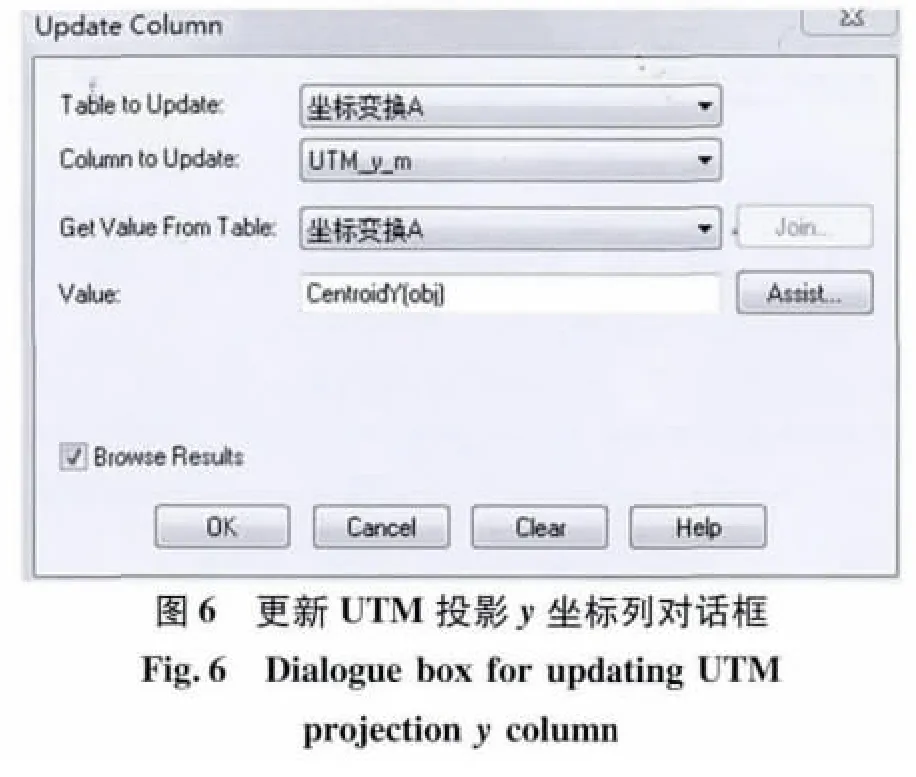
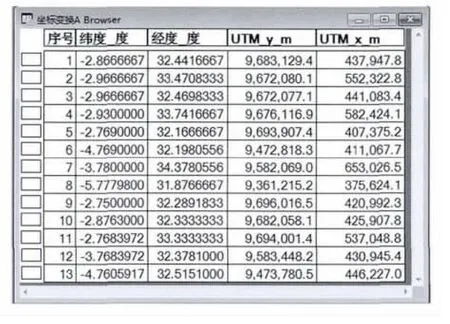
图7 得出的UTM投影x和y坐标对话框Fig.8 Dialogue box for resulted UTM projection x and y coordinates from longitude and latitude

使用中国境内购买的正规汉化版MapInfo®Professional版本10.5求出的TAB文件中，对南半球的点，其数据有时没有对UTM投影y坐标北伪偏移10，000 km校正。使用中国境内销售的正规MapInfo®Professional版本10.5软件时注意此问题，要手工对得出的y坐标数据进行北伪偏移改正。但是在其MAP文件中的实际投影点却无此毛病。发现此问题后，本文采用MapInfo® Professional版本10.5的英文版简易汉化版进行的变换。

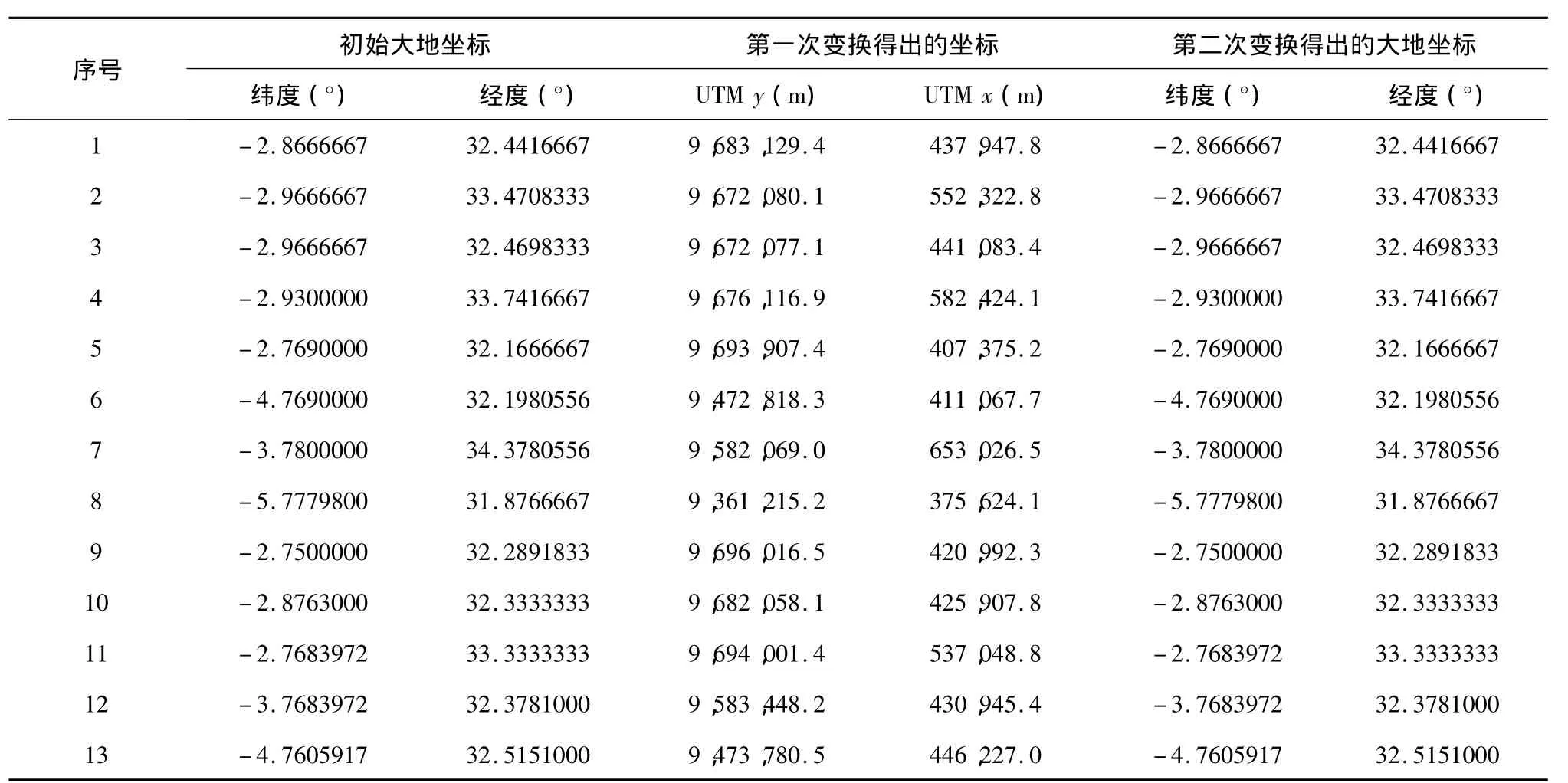
表1 大地坐标和UTM投影坐标变换结果(WGS 84)Table 1 Results of conversion from WGS 84 ellipsiod longitude and latitude to UTM WGS 84 coordinates and vice versa.

6 结论

UTM投影与Gauss-Krüger投影都是正形横墨卡托投影。Gauss-Krüger投影是椭圆柱横正轴切地球椭球体，投影后中央经线长度不变，从投影原点随着纬度和经度增加，投影后的长度、面积等畸变逐渐增大。

UTM投影为椭圆柱横正轴割地球椭球体，从中央经线圆投影比例因子k为0.999 6倍，向两侧k逐渐增大，到距离中央经线179.776 km(WGS 84椭球体)，即经度差1.620 6°，即为两条标准割线圆的位置，该割线圆在UTM投影图上k=1。向外长度以及面积畸变逐渐变大。向南北两极收敛角也逐渐增大，为保证投影精度在一定范围内及使用方便，UTM投影只适用于80°S和84°N的纬度范围内。

两种投影的伪偏移也不同以及x和y表达方式不同。

使用MapInfo®可以很简单快速地实现大地坐标和UTM投影以及Gauss-Krüger投影坐标之间的大批量数据的相互转换。

致谢在论文的撰写过程中得到中国科学院遥感应用研究所刘少创研究员和张烁的宝贵建议，姜高珍和甘凤伟博士以及匿名审稿人等提供了协助，在此表示感谢。

［注释］

① Mercator’s Projection［EB/OL］.http://www.math.ubc.ca/～ israel/m103/mercator/mercator.html.2012 －12 －01.

② 墨卡托投影［EB/OL］.http://baike.baidu.com/view/301981.htm.2012－12－01.

③ World Geodetic System［EB/OL］.http://en.wikipedia.org/wiki/World_Geodetic_System#cite_note－2.2012－12－01.

Chen Wu-tian.2010.Construction survey in countries using UTM projection［J］.Science and Technology Information，(8):36 － 37(in Chinese with English abstract)

Deakin，R.E.，Hunter M.N，Karney C.F.F.2010.The Gauss-Krüger project，Presented at the Victorian Regional Survey Conference［J］.Warrnambool:10 －12

Dorrer E.2003.From Elliptic Arc Length to Gauss-Kriiger Coordinates by Analytical Continuation［M］.in:Geodesy—the challenge of the 3rd millennium，Springer Verlag:91－99

Dozier J..1980.Improved algorithm for calculation of UTM and geodetic coordinates［R］.NOAA Technical Report NEES 81

Han Guo-jian，Di Qiu-sheng，Tan Si-xiu.1994.Differences between UTM projection and Gauss-Krüger projection［J］.Survey and Mapping of Sichuan，(2):51－56(in Chinese)

Kawase K.2011.A general formula for calculating meridian arc length and its application to coordinate conversion in the Gauss-Krüger projection［J］.Bulletin of the Geospatial Information Authority of Japan，59:1－13

Kong Xiang-yuan，Guo Ji-ming.2006.Control Survey［M］.Wuhan:Wuhan University Press:1－150(in Chinese)

Langley R B.1998.The UTM grid system［J］.GPS World，8:46－50

Li S.，Zhang L.，Cui Y.，and Yin X.2003.Relationship and applications of UTM projection and Gauss—Krüger projection，Proceedings of the 21st International Cartographic Conference(ICC)Durban，South Africa，10.16 August 2003.Cartographic Renaissance.Hosted by The International Cartographic Association(ICA)，ISBN:0－958－46093－0 Produced by:Document Transformation Technologies

Liu Ming-bo，Lei Jian-ming，Wei Chan.2010.UTM projection and projection deformation treatment［J］.Hydropower of Northwest，(6):7－9(in Chinese with English abstract)

Lü Xiao-hua，Liu Hong-lin.2002.A comprehensive appraisial of numerical transformation method for map projection［J］.Journal of Institute of Surveying and Mapping，19(2):150－153(in Chinese with English abstract)

Osborne P..2008.The Mercator Projection［M］.Edinburg

Shen Ben-zhong.1986.A new calculation for Mercator transverse projection ellipsoidal coordination［J］.Journal of Xi’an College of Geology，8(1):71－86(in Chinese with English abstract)

Snyder J P.1987.Map projections-A working manual［R］.U.S.Geological Survey Professional Paper 1395，US Government Printing Office

Sun Li-dong.2008.Similarities and differences of Gauss-Krüger projection and Universal Mercator projection［J］.Port Engineering Technology，(5):51 －53(in Chinese with English abstract)

Wang Zheng-mei.2002.A Comparison of Gauss-Krüger projection with transverse perspective cylindrical projection ［J］.Bulletin of Survey and Mapping，(3):11－12(in Chinese with English abstract)

Xia Lanfang，Hu Peng，Huang Meng-long.2007.A numer ical implementation of analytical transformation using map projection［J］.Science of Surveying and Mapping，32(3):69 －71(in Chinese with English abstract)

Xiong Zhong-zhao.2010.Establishment of independent coordinate systems on the UTM projection［J］.Geospatial Information，8(2):41－43(in Chinese with English abstract)

Yang Qi-he.1981.The Gauss-Krüger projection and the Transverse Mercator projection［J］.Bulletin of Survey and Mapping，(6):34 －37(in Chinese with English abstract)

Yang Qi-he.1986.The research of theory and application of map projection transformation ［J］.Journal of PLA Institute of Surveying and Mapping，(1):65－72(in Chinese with English abstract)

Yang Qi-he.1994b.Summarization for theory and method of conformal projection［J］.Journal of Institute of Surveying and Mapping，11(2):133－139(in Chinese with English abstract)

Yang Qi-he.1994b.Summarization for theory and method of conformal projection［J］.Journal of Institute of Surveying and Mapping，11(3):133－139(in Chinese with English abstract)

［附中文参考文献］

陈悟天.2010.使用UTM投影坐标系国家的施工测量［J］.科技资讯，(8):36－37

韩国建，邸秋生，谭思秀.1994.UTM投影和高斯－克吕格投影的差异［J］.四川测绘，(2):51－56

孔祥元，郭际明.2006.控制测量学［M］.武汉:武汉大学出版社:1－150

刘明波，雷建明，韦婵.2010.UTM投影及变形处理［J］.西北水电，(6):7－9

吕晓华，刘宏林.2002.地图投影数值变换方法综合评述［J］.测绘学院学报，19(2):150－153

沈本忠.1986.椭球面横墨卡托投影坐标计算新公式［J］.西安地质学院学报，8(1):71－86

孙立东.2008.高斯－克吕格投影和横轴墨卡托(UTM)投影的异同［J］.港工技术，(5):51－53

王政梅.2002.高斯－克吕格投影与横切圆柱透视投影的比较［J］.测绘通报，(3):11－12

夏兰芳，胡鹏，黄梦龙.2007.地图投影解析变换的数值实现方法［J］.测绘科学，32(3):69－71

熊忠招.2010.浅谈UTM投影下独立坐标系统建立［J］.地理空间信息，8(2):41－43

杨启和.1981.高斯－克吕格投影和横墨卡托投影［J］.测绘通报，(6):34－37