中国工业企业研发效率的波及面*

于长宏， 白 辰

(大连理工大学 管理与经济学部， 大连 116024)

进入21世纪以来，随着全球化的深入发展，国家间的科技竞争不断加剧。2006年《国家中长期科学和技术发展规划纲要(2006—2020)》提出建设创新型国家，此后“增强自主创新能力，通过科技竞争力的提高实现经济结构的转变，实现经济全面协调可持续发展”日益成为全社会关注的话题。在这一背景下，研究与开发(R&D)作为建设“科技竞争力”的主要手段，也受到越来越多的重视。近年来，虽然在科学研究方面投入的资源持续增加，但我国企业在自主创新方面的表现仍然不尽如人意，这主要表现在大量的核心技术和知识产权并不为我国企业所掌握上，说明我国距离创新型国家还有很长的距离。刘和东(2011)认为，创新资源的投入只是创新型国家形成的必要而非充分条件。在建设创新型国家的过程中，R&D等创新资源的投入只是一个方面，对于我国来说，更加重要的是研发活动的投入产出效率，即研发效率[1]。

顾名思义，研发效率就是指研发行为的投入产出关系，即企业投入一单位的研发资源(包括人力、物力等)可以产生多少创新收益(比如新产品、专利等)。研发活动可以提高企业的生产率[2-4]，改善企业的绩效[5-6]，对企业的经营具有重大贡献。那么，研发活动的效率对企业经营的波及面有多大?具体来说，这里所说的波及面主要指研发效率对企业的研发决策、全要素生产率和盈利能力的影响。对于研发效率的波及面，即研发效率对于研发决策、生产率和盈利的影响，国内外的研究均较少涉及。本文主要研究研发效率如何影响研发决策、生产率和盈利水平。

国内外关于研发效率的研究主要是分析影响研发效率的因素。从国内研究来看，影响我国企业研发效率的因素主要有三大类：首先是企业的所有制结构[7-9]，比如周立群等(2009)检验了我国高科技企业中国有控股和三资企业的研发效率分布，发现产权制度、企业规模、市场结构和企业消化吸收能力等因素对研发效率的影响较为明显[7]。其次是企业内部治理结构，张长征等(2006)认为，在成本异质性的假定下，最优的报酬结构取决于研发人员对于经济报酬和非经济报酬的感知程度，给予员工权变的薪酬组合可以改善整体的研发效率[10]。最后是产业、政策等外部因素，比如原毅军、耿殿贺(2010)认为，企业规模、产业结构、政策环境以及企业研发经费是影响装备制造业研发效率的主要因素，并提出通过构建横向与纵向的技术合作机制来提高研发效率[11]。

与国内学者不同，国外的研究更关心微观因素对企业研发效率的影响。比如Mogens等(2003)的研究指出，由大股东控股的企业与其他股权结构的企业相比并没有表现出明显的效率优势[12]。Mario(2006)探讨了互联网对企业研发效率的作用，认为互联网的两大功能(搜索和共享)可以提升企业研发的成本、时间和质量效率，从而带来研发效率和吸收能力的提高[13]。Cullmann等(2010)对1995—2004年数据的实证研究表明，如果政策环境中存在限制竞争的行业进入限制，那么相关企业的研发效率和创新激励都会明显下降[14]。Zhang等(2003)的研究认为，对于中国企业来说，所有制结构和研发效率的关系十分密切，他通过测算8 341家在中国经营的企业的研发效率，认为外国企业比中国企业的研发效率更高[15]。

一、模型构建

假设企业生产两种产品——成熟产品和新产品，并且新产品的生产完全取决于企业的R&D活动，两种产品的生产函数满足Cobb-Douglas形式，分别为

(1)

式中：Y1，Y2——成熟产品和新产品的产值；

K1，L1——企业生产成熟产品所使用的资本和人力；

K2，L2——企业为生产新产品所投入的研发资本和人力。

式(1)中，αi+βi=μi。利润最大化条件为

maxK1，L1，K2，L2π=Y1+Y2-(K1+K2)-w(L1+L2)=

Y0-K0-wL0

(2)

式中：w——企业的工资水平；

Y0——企业的总产值，等于成熟产品和新产品的产值之和；

K0，L0——企业投入的资本总额，K0=K1+K2，L0=L1+L2。

企业总产值Y同样满足Cobb-Douglas形式，公式为

(3)

(4)

RDI对研发效率θ2求导得

(5)

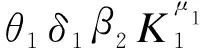
下面考察企业的生产率、利润与研发效率的关系。因为企业的总产值等于成熟产品和新产品产值之和，即Y0=Y1+Y2。将极值条件代入式(5)整理可得

(6)

显然∂θ0/∂θ2>0，所以企业的生产率是研发效率的增函数。另外，企业的利润函数为π=Y0-K0-wL0，所以相应的利润率为

(7)

利润率PR显然是生产率的增函数。根据复合函数的性质，PR同时也是研发效率的增函数。因此，研发效率具有提高企业利润水平的作用。

命题研发效率不仅能够影响企业的研发决策，而且对于提升企业的绩效(生产率和利润)也有正面作用。

二、数据来源

本文主要使用了2007年中国企业数据库中的工业企业样本，该数据库囊括了我国国有及非国有规模以上工业企业的主要财务信息，其中本文使用的数据变量有工业增加值、企业利润、固定资产总值、研发投入、从业人数、职工工资、经营时间、出口规模、管理费用、职工培训费用、所属地域等。按照二分位划分方法，我国制造业的行业代码和行业名称的对照如表1所示。

样本企业来自于我国31个省、自治区和直辖市。中国国家统计局对于我国行政区域的划分方法是：北京、天津、河北、上海、江苏、浙江、福建、山东、广东和海南被划为东部；山西、安徽、江西、河南、湖北和湖南归入中部；辽宁、吉林和黑龙江属于东北；其他省份为西部。按照这一划分，样本中位于东部、中部、西部和东北地区的企业所占的比重分别为72.38%、9.51%、12.30%和5.81%。此外，《中国工业企业数据库》将企业按照登记注册类别划分为23类，包括国有企业、集体企业、股份合作企业、联营企业、私营企业、外商投资企业以及港澳台投资企业等类别。本文将国有企业、集体企业、联营企业和国有独资公司均划归为“国有经济”，将私营企业划归为“私营经济”，外商投资企业和港澳台投资企业则划归为“外资经济”。在样本中，国有经济、私营经济和外资经济所占的比例分别为12.55%、57.92%和29.53%。

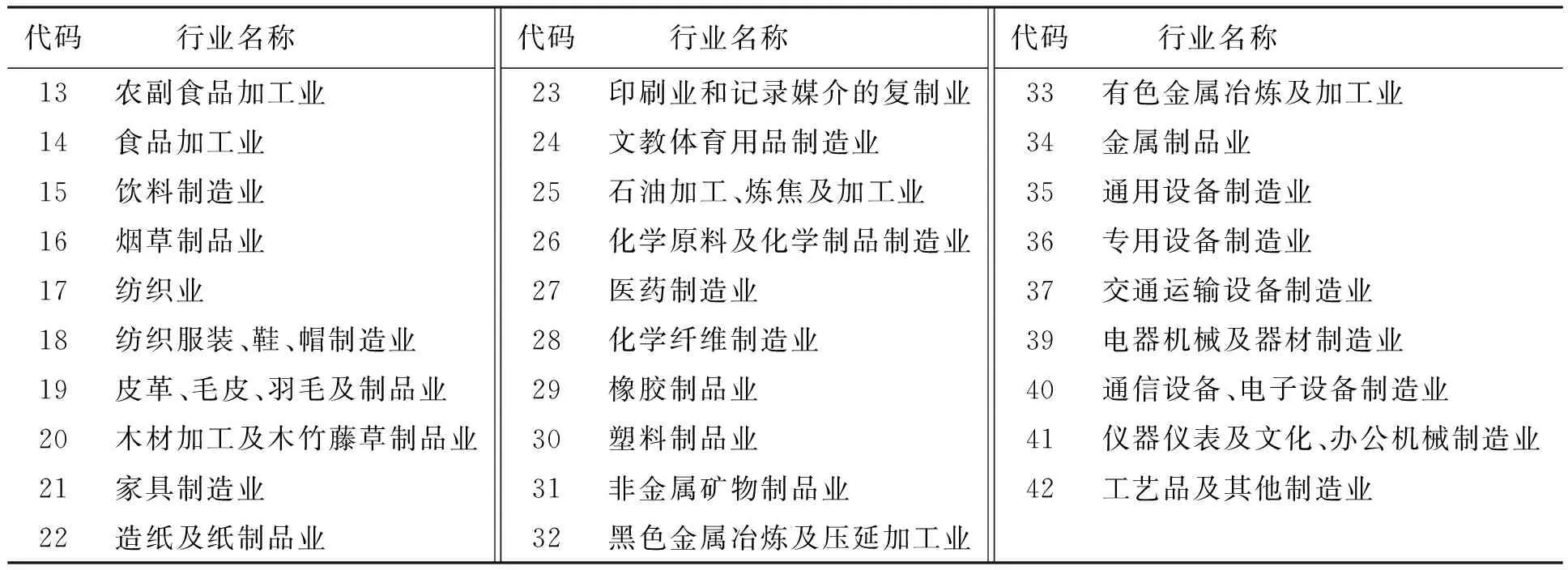
表1 我国制造业行业代码和行业名称

资料来源：中国工业企业数据库。

在应用数据库中的数据之前，还要对其进行筛选。具体的步骤如下：(1)删除明显违背事实的企业样本。由于统计上的错误，有时会遇到非正的工业增加值、固定资产总值、企业从业人数或研发支出，为了保证结果的准确性，本文将这样的样本予以删除。(2)研究中需要用到新产品销售收入，因此，在2007年没有新产品销售收入的样本不予考虑。(3)仅保留进行研发投入的企业的数据，其余的样本不采用。(4)仅保留从业人数在8人以上的企业样本，其余的不予考虑。(5)仅保留正常营业的企业样本，处于其他营业状态诸如停业、筹建、撤销等的企业予以剔除。

三、中国工业企业的研发效率

为了度量中国工业企业的研发效率，使用随机前沿分析(SFA)方法。该方法由Meeusen和Van den Broeck(1977)提出[16]，模型为

Yi=Xiβ+(Vi-Ui) (i=1，2，…，N)

(8)

式中：Yi——企业i的实际产量；

Xi——企业i各项投入的k阶列向量；

β——未知参数向量；

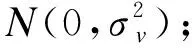
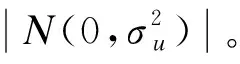
(9)

式中：Yi——企业的实际产出；

Yif——不存在非效率因素时的研发产出函数；

Ui——非效率项。

研发产出函数有两种较为常见的形式，分别是Cobb-Douglas函数和超越生产函数。前者需要满足技术中性和产出弹性固定的假设；后者虽然形式较为复杂，但不需要太多的假设。因此，本文使用超越生产函数的SFA模型来测算企业的研发效率。根据Coelli(1996)的研究，假定研发产出函数满足

lnYi=β0+β1lnKi+β2lnLi+β3(lnKi)2+

β4(lnLi)2+β5lnKilnLi+(Vi-Ui)

(10)

式中：Yi——企业的研发产出，本文使用企业在2007年的新产品销售收入来度量Yi；

Ki，Li——企业投入的研发资本和人力。

关于企业投入的研发资本，也就是当年企业所拥有的研发资本存量，Griliches(1984)认为，一般可以用此前几年内企业研发投入的现值来表示它。除此之外，还可以使用永续盘存法(PIM)来计量研发资本存量。根据吴延兵(2006)的研究，运用PIM方法表示的研发资本存量满足Kt=(1-δ)Kt-1+Rt，其中K、δ表示R&D资本存量和R&D资本折旧率。假设R&D资本存量以稳定的增长率g增长，则资本存量也可表示为Kt=(1+g)Kt-1，消掉Kt-1项并取自然对数得lnKt=lnRt+ln[(δ+g)/(1+g)]。而Pakes和Schankerman(1984)认为，由于知识的更新速度很快，所以R&D资本的折旧率很高，如果将δ看作接近于1，那么就有lnKt≈lnRt，即在一定时期内的R&D资本存量近似地等于当期的R&D投入规模。因为本文使用的是横截面数据，所以使用企业当年的R&D支出代表R&D资本存量，即企业的研发资本投入。另外，由于没有关于企业研发人员的直接数据，本文使用调整后的企业从业人数来代替研发人员人数，具体方法是用《中国科技统计年鉴》上各行业工程师和科学家占从业人员总数的比例乘以该行业内企业的总从业人数得出。运用Frontier 4.1计算随机前沿生产函数，可以得到每个企业研发投入和研发产出之间的转化关系，即研发效率，极大似然估计结果如表2所示。

表2 随机前沿分析估计结果

注：***代表因变量的估计系数在1%的水平上显著地异于零。

由表2可以看出，单边误差似然比检验值很大，因此极大似然估计结果没有被拒绝，可以采用。达到0.938 9的γ值说明非效率因素对我国工业企业研发产出的影响很大，这进一步确认了采用随机前沿分析的合理性。就研发效率的估计结果来说，我国工业企业2007年的研发效率平均值仅为0.413 6，即实际创新产出还不到生产边界的一半，表明我国企业的研发活动受到各种非效率因素的明显影响。

分别计算各行业以及各省份研发效率的平均值，并按照由高到低降序排列可以得到图1、2中的曲线。

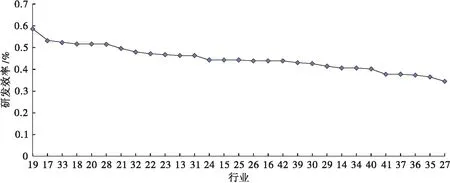
图1 我国工业行业研发效率平均值

图2 各省份平均研发效率

就行业来说，各行业的研发效率存在明显区别，研发效率最高的是皮革制品业(平均研发效率为0.585 144)，而最低的是医药制造业(平均研发效率为0.343 750)。总体来说，我国研发效率较高的行业大多是技术较为简单的轻工业，比如行业19(皮革制品业)和行业17(纺织业)；或者是资源密集的重工业，比如行业32(黑色金属加工业)和行业33(有色金属加工业)。相比较而言，技术密集的装备制造业(比如专用设备制造业)和高附加值化学工业(比如医药制造业)的研发效率普遍较低。

就省份来说，图2中的曲线明确地揭示了一个规律：东部省份的研发效率普遍较高，其次是中部，而西部的研发效率最低。沈坤荣等(2009)认为，市场竞争程度和外国直接投资(FDI)可以在较长的时期内提高内资企业的研发效率。相对于其他地区来说，东部地区由于地理位置、历史、政策等原因，其市场化程度更高且吸收了大量外资，因而具有更高的研发效率。就这一点来说，西部地区刚好相反，因而其研发效率普遍落后于东部和中部。

四、实证检验

结合前面得到的企业研发效率，运用筛选后的数据样本探讨研发效率在三个方向上对我国工业企业经营情况的波及程度：(1)研发效率对企业研发决策的影响；(2)研发效率对企业生产率的影响；(3)研发效率对企业盈利能力的影响。

1. 研发效率对研发决策的影响

引入代表企业研发强度的变量RDI，RDI等于企业2007年的研发支出除以其工业产值再取自然对数。除了代表研发效率的自然对数的变量RDE之外，还应加入其他的自变量以提高估计的准确性。根据数据库的特点并参考汤二子等(2011)[19-20]的相关分析，引入如下解释变量：(1)企业利润PRO。该变量反映了企业创造财富的能力，同时决定了企业进行研发投入的能力，因此很有可能会影响企业关于研发强度的决策。因为企业利润可能为负值，所以让PRO=sgn(profit)·ln(|profit|+1)，其中profit为企业当年利润。(2)企业规模SCALE。从经验上来说，规模较大的企业一般更有能力投入研发。本文使用企业的固定资产总值作为SCALE的计量基础。SCALE等于企业固定资产总值加1再取自然对数。(3)出口规模EX。该变量由企业当年出口规模加1再取自然对数得到。(4)员工培训支出TR。企业培训员工是为了使人力资本得到增值从而获得更高的生产效率，这样的企业可能更愿意进行研发投入。该变量由企业员工教育费用加1之后取自然对数得到。(5)企业年龄AGE。(6)管理支出MAN。作为解释变量，因为管理支出间接反映了企业的经营效率，所以很可能与研发效率相关。此外，管理费用也可能影响企业的研发决策。因为如果企业将过多的资源用于管理支出，就不可能有多余的能力投资于研发。MAN为企业管理费用加1再取自然对数。综上，假设实证模型的形式为

RDI=C+α1RDE+α2PRO+α3SCALE+α4EX+α5TR+α6AGE+α7MAN+control

(11)

式中，control包括行业、地区和企业所有制结构等信息。估计结果如表3所示。

ln RDI的回归结果显示，研发效率对企业的研发强度具有显著的促进作用。这就是说，拥有较高研发效率的企业更加倾向于进行高强度的研发活动，这个事实与模型的结论相一致。不出意外地，利润水平、企业规模、出口规模对企业研发强度的偏效应均为正。员工培训支出的系数为正，说明重视人力资本的企业进行研发的强度更大。这是因为员工通过培训提高了自身技能，使得企业的创新成果能更好地应用于生产中。管理支出MAN的符号为负，意味着高强度的研发活动与灵活、高效的企业制度相对应。如果没有整体的经营效率作保障，企业无法为R&D提供有力的支持。

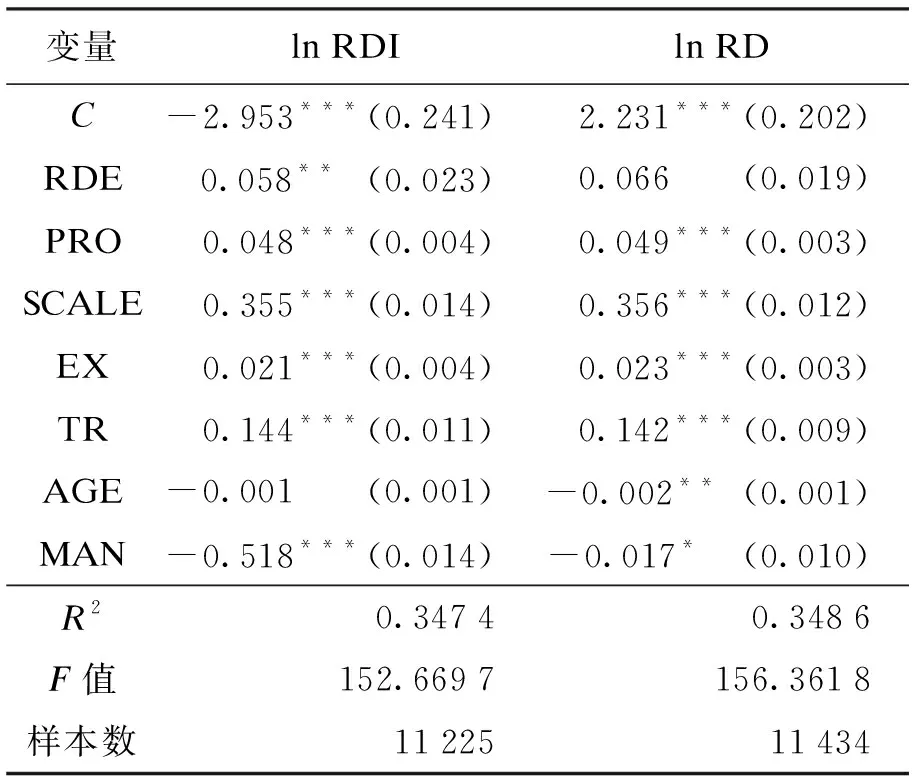
表3 研发效率对研发决策的影响

接下来要进一步考察研发效率对企业研发支出总额的影响。以RD作为反映企业研发支出的因变量，RD等于研发支出的自然对数。建立回归模型

RD=C+α1RDE+α2PRO+α3SCALE+α4EX+α5TR+α6AGE+α7MAN+control

(12)

从ln RD的结果来看，研发效率对企业研发决策的影响不仅是增加了研发强度，还明显扩大了企业的研发规模。利润水平、企业规模和出口规模对于研发规模的影响为正，说明只有达到一定规模和经营绩效的企业才会进行研发投入。员工培训支出TR与管理费用MAN的符号与方程(11)的结果相同，对此的解释也相类似。

结论1对于我国工业企业来说，研发效率高的企业进行研发投入的意愿更大。

2. 研发效率对生产率的影响

一般来说，人们经常使用的测量生产率的方法有三种：第一种方法是近似全要素生产率ATFP(Griliches等，1990)。这里ATFP=ln(Q/L)-sln(K/L)，其中，Q，K，L分别是企业的工业增加值、固定资产总值和从业人数。第二种方法是劳动生产率LTFP。假设LTFP=ln(Q/L)，其中Q为工业增加值，L为从业人数。这两种方法虽然简单易行但却各有缺陷：ATFP假定企业的生产函数为规模报酬不变的Cobb-Douglas形式，这一点与我国的实际并不相符；LTFP仅考虑企业劳动投入，所以无法全面衡量企业的生产效率。因此，本文将使用第三种方法，即于洪霞等(2011)提出的以全要素生产率作为企业生产率的标准，用企业产量的自然对数lnQ对企业使用的资本和劳动的自然对数lnK和lnL作无截距项的回归，所得的残差即为企业全要素生产率的近似对数值ln TFP。

对全要素生产率指标进行实证检验时所使用的解释变量包括研发效率RDE、研发支出RD、利润水平PRO、企业规模SCALE、出口规模EX、员工培训支出TR、企业年龄AGE、管理支出MAN，相关的数据处理方法与之前相同。在此基础上建立实证方程

ln TFP=C+α1RDE+α2RD+α2RD·RDE+α3PRO+α4SCALE+α5EX+α6TR+α7AGE+α8MAN+control

(13)

研发效率对生产率的影响如表4所示。从表4中A列的结果来看，研发效率的提高对企业全要素生产率具有正的影响，说明提升研发效率不仅可以提高企业单位研发投入的产出，还可以提升企业整体的价值创造能力。A列中还有一个奇怪的现象——研发投入对于生产率的偏效应竟然为负。为了进一步考察研发投入对生产率的影响，在方程(13)中又加入了研发投入RD的平方项，相关的回归结果整理在表4的B列中。可见研发投入规模RD和其平方项均未通过显著性检验，这是由多重共线性造成的。事实上，如果仅仅保留RD或者RD的平方项，它们在方程中的回归系数都是显著的，而且这两项的系数联合显著，因此B列中的结果仍然具有说服力。RD的平方项系数为正，说明企业的研发投入只有达到一定的规模之后才有可能促进企业生产率的提高，小规模的研发投入反而可能降低企业的生产率。这一结论说明创新活动与企业投入规模之间的关系与Schumpeter的观点大体一致。

为了进一步探究研发效率、研发投入与企业生产率之间的关系，在方程中加入了研发效率与研发规模的交叉项RD·RDE，回归的结果在表4的C列中显示。可见，RD的系数仍然为负，但交叉项RD·RDE的系数为正。这说明对于规模较小的企业来说，只要它的研发效率足够高，那么小规模的研发投入仍然可以促进企业生产率的提高。这一结论十分重要，因为它可以解释创新活动向中小企业分散这一现实——中小企业虽然不能和大企业一样进行大规模的研发投入，但是机制灵活、研发效率高。正是因为具有了较高的研发效率，中小企业有限的研发规模才能提高而不是降低其生产率。

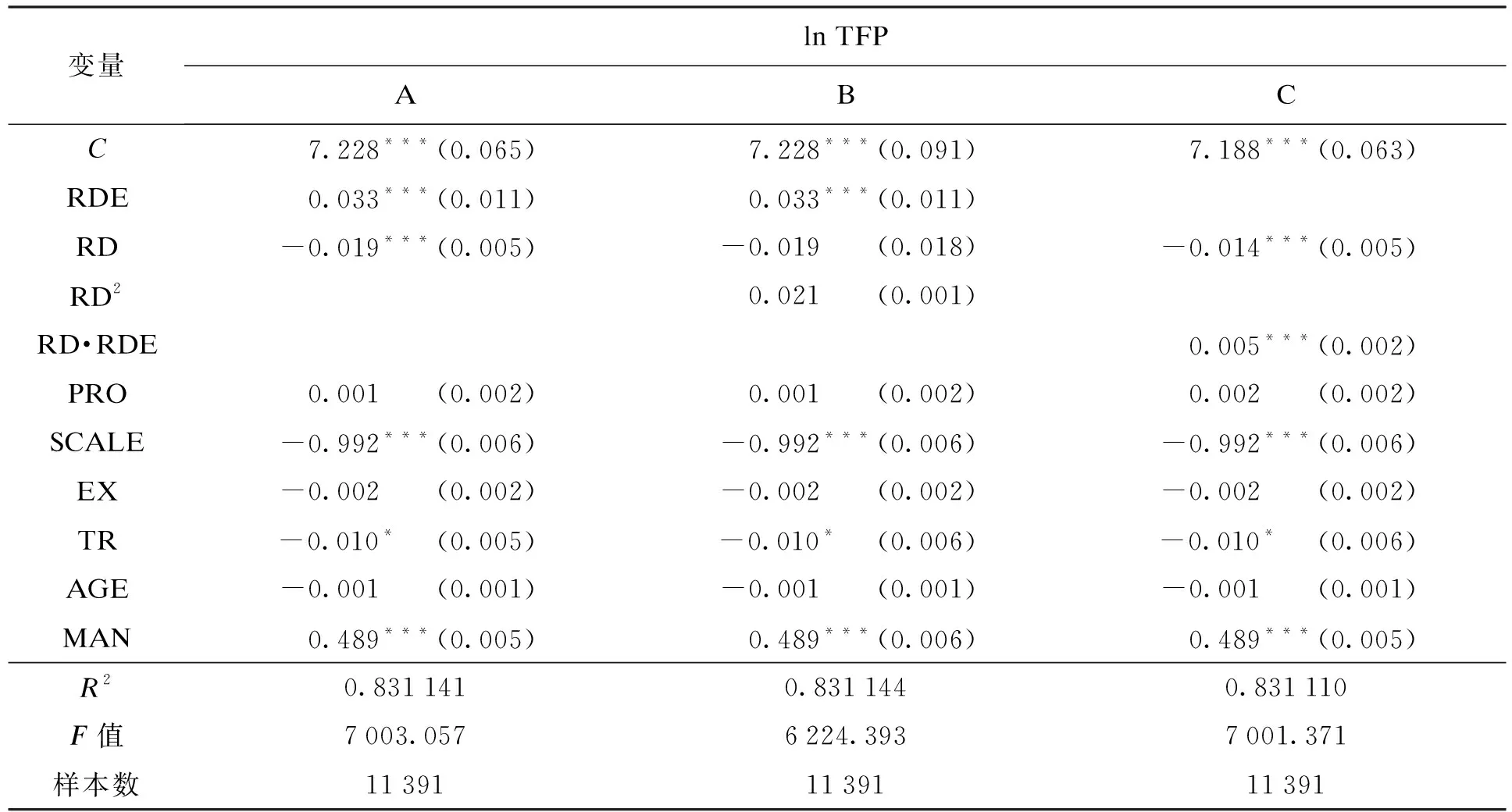
表4 研发效率对生产率的影响

结论2研发效率与企业的生产率密切相关，主要体现在两个方面：研发效率较高的企业通常具备较高的全要素生产率；研发效率明显提高了企业研发投资的利用效能，使有限的研发投入能更有效地提升企业的生产率。

3. 研发效率对盈利能力的影响

分别将企业利润PRO和利润率PR作为因变量进行检验。这里的利润率PR设定为销售利润率，等于利润总额除以工业销售总额。除了之前引入的因变量RDE、PRO、SCALE、EX、TR、AGE和MAN之外，还包括企业的研发支出RD。考虑到研发支出和研发效率关系密切并且可能影响企业的利润，这样做是必要的。相关的数据处理方式与上文相同。根据这些变量，设定回归方程的形式为

Profiting=C+α1RDE+α2RD+α3SCALE+α4EX+α5TR+α6AGE+α7MAN+control

(14)

Profiting分别为企业利润PRO和利润率PR，control项包含的内容如前。相应结果整理后如表5所示。

由表5可见，研发投入对企业利润水平和利润率具有显著的正影响。研发效率对于利润的偏效应甚至比研发规模还要大，这是因为研发效率通过两种途径影响企业的利润水平：研发效率的提高使得同样的研发投入可以获取更多的研发产出，从而增加了企业利润；研发效率的提高刺激企业继续加大研发投入，这一部分投入又可以增加利润。这两个原因决定了研发效率对企业的盈利能力具有较大的影响。

表5 研发效率对盈利能力的影响

结论3研发效率对企业盈利能力改善的影响是不可忽视的，它的作用甚至比研发投入本身更加重要。

五、结 论

创新是经济持续增长的不竭动力，Schumpe-ter(1943)指出，创新在市场经济中的地位与价格体系和竞争制度同样重要。作为社会创新的主要载体，企业的研发活动越来越受到重视。迄今为止，人们已经从很多角度研究了研发活动对企业经营绩效的影响。尽管如此，现有的研究在研发效率对企业研发决策、生产率和盈利能力的影响方面尚不够丰富，本文在这方面提供了经验证据。

本文利用相关数据测算了我国工业企业的研发效率，在此基础上检验了研发效率对企业研发决策、生产率和盈利能力的偏效应。研究发现：(1)研发效率高的企业对于创新活动往往更加积极，这似乎说明企业的资源会自发地流向具有较高效率的部门；(2)对研发效率与生产率的检验表明了两者之间的高度相关性——研发效率提高了研发投资的效率，所以研发效率高的企业其生产率通常也比较高；(3)研发效率的提高可以明显改善企业的盈利能力。就我国企业来说，提高研发效率比同等幅度地扩大研发投资规模更能提高企业的利润总额和利润率。

参考文献：

[1]刘和东.中国区域研发效率及其影响因素研究：基于随机前沿函数的实证分析 [J].科学学研究，2011(4)：548-556.

[2]Griliches Z.Productivity，R&D and basic research at the firm level in the 1970s [J].American Economic Review，1986，76(1)：141-154.

[3]Mairesse J，Sassenou M.R&D and productivity：a survey of econometric studies at the firm level [J].Science-Technology-Industry Review，1991(8)：9-43.

[4]Hall B H，Mairesse J.Exploring the relationship between R&D and productivity in French manufacturing firms [R].NBER：Institute for Prospective and Technological Studies，1992.

[5]Goto A，Suzuki K.R&D capital，rate of return on R&D investment and spillover of R&D in Japanese manufacturing industries [J].Review of Economics and Statistics，1989，71(4)：555-564.

[6]Wang E.R&D efficiency and economic performance：a cross-country analysis using the stochastic frontier app-roach [J].Journal of Policy Modeling，2007，29(1)：345-360.

[7]周立群，邓路.企业所有权性质与研发效率：基于随机前沿函数的高技术产业实证研究 [J].当代经济科学，2009(4)：70-75.

[8]张永庆，刘清华，徐炎.中国医药制造业研发效率及影响因素 [J].中国科技论坛，2011(1)：70-74.

[9]朱有为，徐康宁.中国高技术产业研发效率的实证研究 [J].中国工业经济，2006(11)：38-45.

[10]张长征，李怀祖.研发团队异质性与报酬模式对研发效率的影响分析 [J].科学学与科学技术管理，2006(3)：36-39.

[11]原毅军，耿殿贺.中国装备制造业技术研发效率的实证研究 [J].中国软科学，2010(3)：51-57.

[12]Mogens D H，Erik M，Valdemar S.Efficiency，R&D and ownership：some empirical evidence [J].International Journal of Production Economoics，2003，38(1)：85-94.

[13]Mario I K.The impact of the internet on R&D efficiency：theory and evidence [J].Technovation，2006，26(3)：827-835.

[14]Cullmann A，Schmidt-Ehmcke J，Zloczysti P.R&D efficiency and barriers to entry：a two stage semi-parametric DEA approach [R].London：Centre for Economic Policy Research，2010.

[15]Zhang A M，Zhang Y M，Zhao R.A study of the R&D efficiency and productivity of Chinese firms [J].Journal of Comparative Economics，2003，31(4)：444-464.

[16]Meeusen W，Broeck V J.Efficiency estimation from Cobb-Douglas production functions with composed error [J].International Economic Review，1977，18(4)：435-444.

[17]Battese G，Coelli T.A model for technical inefficiency effects in a stochastic frontier production function for panel data [J].Empirical Economics，1995，20(3)：325-332.

[18]Battese G，Corra G.Estimation of a production frontier model：with application to pastoral zone of eastern Australia [J].Australia Journal of Agricultural Economics，1977，21(2)：169-179.

[19]Coelli T.A guide to frontier version 4.1：a computer program for stochastic frontier production and cost function estimation [R].London：Centre for Econo-mic Policy Research，1996.

[20]汤二子，王瑞东，刘海洋.研发对企业盈利决定机制的研究：基于一致性生产率角度的分析 [J].科学学研究，2012(1)：124-133.