体-杆耦合法在预应力混凝土结构计算中的应用
2013-12-17何光宇
何光宇
(中国水电顾问集团成都勘测设计研究院,四川 成都 610072)
1 前 言
预应力混凝土结构在土木工程中应用广泛。 然而,在以往的分析中,把预应力筋(锚索)作用力用静力等效荷载作用于结构上,该方法忽略了混凝土与预应力钢束的位移协调性,误差大,同时建模过程复杂。因此,有必要寻求一种简单、有效的计算预应力结构的方法。
ANSYS是我国广泛应用的有限元计算软件。 本文提出一种新的分析模型:使用有初应力的空间杆单元来模拟预应力束;以独立建模耦合法为理论基础,在ANSYS中用Solid65单元模拟普通钢筋混凝土,用Link8单元模拟预应力钢绞线[1],用节点耦合模拟预应力筋与混凝土之间的相互作用。本方法适用于预应力筋与混凝土无相对滑动的情况。 该方法比较简单,只需几种单元和实常数即可,同时可以模拟预应力的损失。可以利用杆单元模拟任意形状的预应力筋(锚索)。
2 计算原理
2.1 预应力混凝土分析中预应力的处理
对于有初应力的空间杆单元:
[σ]=[D][ε]+[σ0]
(1)
式中 [σ]、[ε]、[σ0]——分别为应力矩阵、应变
矩阵和初应力矩阵;
[D]——为弹性矩阵。
ANSYS软件没有直接赋予杆单元初应力的方法,本文使用在杆单元中引入温度差的方法来对杆单元施加初始应力[2]。假设σ0是杆单元的期望预应力,E是杆单元的弹性模量,α是材料的热膨胀系数,ΔT是数值模拟中所需的温度差:
(2)
则杆单元中的实际应力为:
[σ]=[D][ε]+αE[ΔT]
(3)
调整温度差就能实现杆单元中不同预应力水平。
2.2 节点耦合理论[2-3]
将钢筋混凝土作为普通块体单元,预应力筋作为空间杆单元,预应力筋和钢筋混凝土的相互作用通过体-杆组合单元的节点耦合来实现。
图1为块体单元内含有一个杆单元的体-杆组合单元。
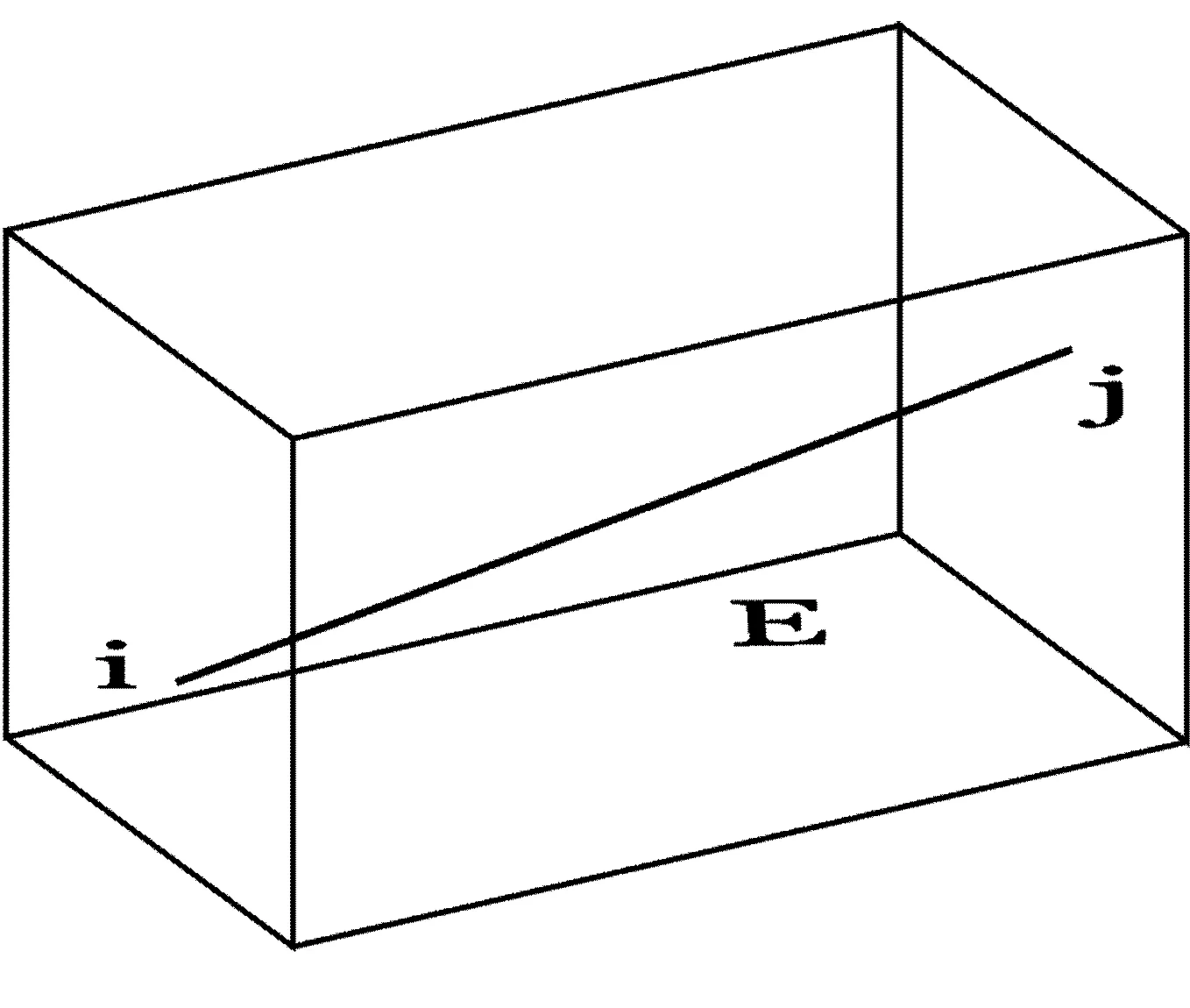
图1 体—杆的组合单元
杆单元节点i、j位于体单元内部,设{δB}e为整体坐标系下杆单元节点位移向量,{δv}e为整体坐标系下块体单元的节点位移向量。
由位移协调性,杆单元节点位移向量{δB}e可由该节点所在的块体单元E的节点位移向量{δv}e插值得到:
{δB}e={N}{δv}e
(4)
式中 {N}——为块体单元的插值形函数矩阵。
设{F}e为杆单元在整体坐标系下与节点位移向量{δB}e对应的节点力,[kB]e为杆单元在整体坐标系下的刚度矩阵,{F}e与{δB}e满足以下关系:
[kB]e{δB}e={F}e
(5)
杆单元的系统势能为:
(6)
将式(4)代入式(6)中,得:
(7)
根据最小势能原理,δ∏p=0,可以求得:
[N]T[kB]e[N]{δv}e=[N]T{F}e
(8)
简写为:
(9)

(10)
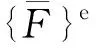
(11)
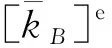
(12)
最后,对预应力钢筋混凝土结构求解:
[k]
{δ}={F}
(13)
式中 [k]——为结构的总体刚度矩阵;
{δ}——为节点自由度矢量;
{F}——为总的外荷载矢量。
预应力筋杆单元对混凝土体单元存在挖空现象,可以通过折减预应力筋杆单元的弹性模量来实现。用Es、Ec分别表示预应力筋和钢筋混凝土的弹性模量,计算时取E=Es-Ec为体—杆组合单元时的预应力筋的弹性模量。
3 预应力混凝土的建模[4]
3.1 预应力结构的建模方法
在ANSYS中,预应力混凝土分析采用实体力筋法。所谓实体力筋法就是用solid65模拟普通钢筋混凝土,而link8模拟预应力筋(锚索)。 实体力筋法将混凝土和预应力筋划分为不同的单元,预应力数值的模拟可以采用温度差实现。该方法比较简单,只需几种单元和实常数即可,同时可以模拟预应力的损失,利用杆单元模拟任意形状的预应力筋(锚索)。
3.2 独立建模耦合法的处理步骤
独立建模耦合法的基本思想是实体和预应力筋独立建几何模型,分别划分单元,然后采用耦合方程将力筋单元和实体单元联系起来,这种方法是基于有限元模型的处理。 ANSYS中利用APDL语言[4]编制的预应力混凝土结构计算程序的流程见图2。
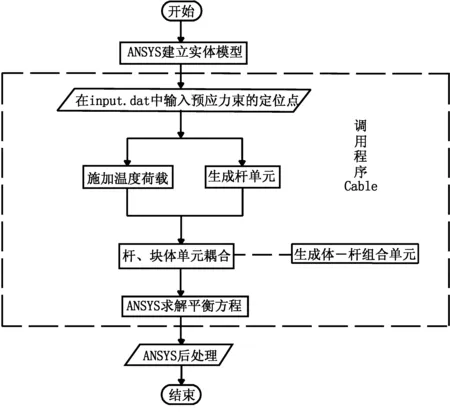
图2 预应力混凝土结构计算流程
!程序中温度荷载大小:temp0=-σ0/(α*E)
!对钢索施加温度荷载命令:
bfl,all,temp,temp0
allsel
!钢索节点和混凝土节点进行偶合命令:
ESEL,S,TYPE,,1,1,1 !选择非钢索单元
ALLSEL,BELOW,ELEM
*dim,nodec,array,ndinqr(0,14)-(nodemax+1)+1,1,1 !和钢索节点对应于最近节点
*do,i,nodemax+1,ndinqr(0,14)
nodec(i-nodemax)=nnear(i)
*enddo
allsel
*do,i,nodemax+1,ndinqr(0,14) !进行ux偶合
nodec0=nodec(i-nodemax)
cp,next,ux,i,nodec0
*enddo
!进行uy、uz偶合,同ux偶合类似。
这种方法建模特别简单,耦合处理也比较简单,是解决预应力筋线形复杂且预应力筋数量很多时的最佳方法。
4 算 例
应用ANSYS软件,及预应力混凝土结构计算程序Cable对某预应力混凝土梁进行应力变形分析。
4.1 基本资料[5]
一根计算跨径为l=20m的预应力混凝土简支梁,截面尺寸布置见图3。梁内配有抛物线形预应力筋,跨中偏心距e=350mm,预加力Np=1 125KN,简支梁受均布荷载为q=11.25kN/m;混凝土弹性模量Ec=3 200MPa,泊松比μ=0.167。预应力钢索的弹性模量Es=1.95×105MPa。
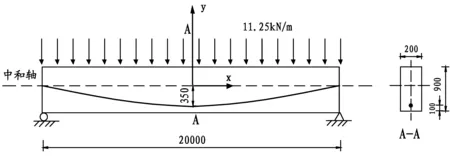
图3 预应力简支梁 (单位:mm)
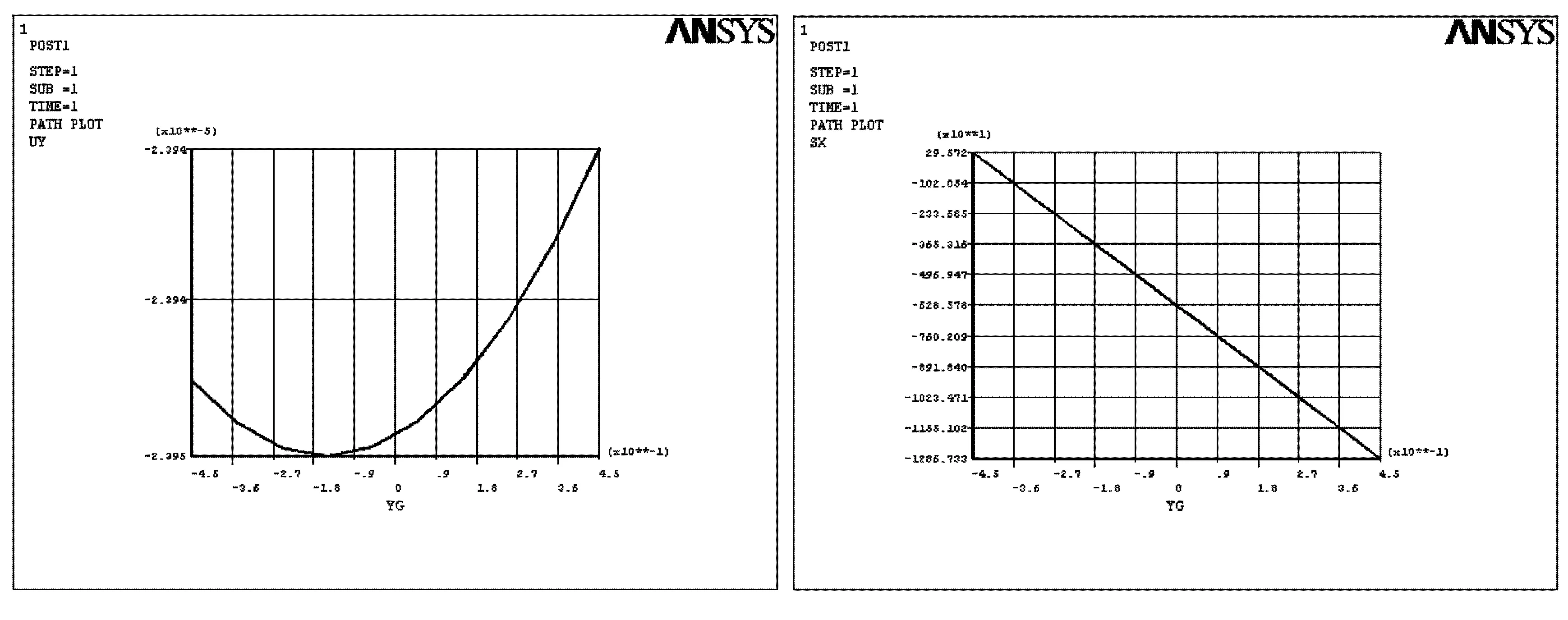
图4 本模型A-A截面应力值 图5 本模型 A-A截面挠度值
4.2 计算结果
应用ANSYS后处理模块,得到A-A界面的应力、变形映射值如图4、5所示,计算结果见表1。

表1 计算结果比较
5 结 语
算例表明,本文采用的实体力筋法和体-杆节点耦合法原理准确,对ANSYS二次开发计算结果精确,程序开发是成功的,克服了ANSYS软件只能采用等效荷载法计算预应力钢筋混凝土结构且误差大的不足,同时简化了有限元的建模过程。
[1] ANSYS高级技术分析指南[M]. ANSYS中国,2001.
[2] 朱伯芳.有限单元法原理与应用[M]. 中国水利水电出版社,2004,19-26:55-64.
[3] 周志祥.高等钢筋混凝土结构[M]. 人民交通出版社,2002,268-277.
[4] 博弈创作室,APDL参数化有限元分析技术及其应用实例[M]. 水利水电出版社,2003.
[5] 李国平.预应力混凝土结构设计原理[M].人民交通出版社,2000: 149-152.
