基于有限元法的冷缩电缆终端缺陷形态特征与局部放电特性分析

, ， ，灏颖， ,

(1. 西南石油大学电气信息学院,四川 成都 610500；2. 国网成都供电公司，四川 成都 610000)

0 前 言

在电缆终端，由于剥除半导电屏蔽层和铜屏蔽层，导致屏蔽层断口处局部电场畸变，场强过大，容易引起局部放电。为了改善局部场强局部集中，常使用应力锥或应力管来疏散应力，改变局部电场分布，降低局部场强。电缆终端在安装时，由于操作人员操作不规范，很容易产生半导电层或绝缘层割伤、应力锥移位、杂质气泡及应力锥凹陷等缺陷，在终端长期运行后，常使其产生局部放电并引发击穿闪络的事故[1]。大量数据表明，局部放电是造成电缆绝缘破坏的主要原因之一，而电缆附件则是其中最薄弱的环节。因此，对电缆附件缺陷模型局部放电的研究具有重要意义。国内外对电缆终端的研究包括传感器及检测方法的研究[2]、数学或软件建模仿真[3-4]、对放电数据的挖掘故障诊断及特征识别[5]和模拟放电缺陷进行局部放电实验[6-9]。当前主要的信号处理方法有小波分析及其衍生算法、K-means聚类算法、模式识别方法、支持向量机理论、分形、Weibull变换等。

目前，对电缆终端缺陷间隙大小与局放程度关系研究的论文还比较少。T.Asokan[10]通过自制的叶片电极微间隙，研究了不同叶片电极组合情况下的击穿强度和局放特性。从其研究中可知，微间隙在小于1 000 μm时已经不再满足帕邢定律，且随间隙的减小，场强呈现增大趋势。他们模拟了电极间的气隙，并未在实际电缆附件或电力设备中进行气隙缺陷的仿真及实验验证。H.Illias通过建立一个球形介质腔[11]，利用有限元仿真和试验的方式研究了不同直径和位置的球形腔在电极之间的电场分布及放电特征。由于实际电缆附件的外形及内部特征的复杂性以及应力锥和铜屏蔽层的使用，有必要对电缆附件的内部缺陷的形态特征与局部放电特性间的关系进行研究。文献[6]模拟了10 kV电缆终端主绝缘不同宽度的轴向空气隙缺陷的电场分布并进行了试验验证，文献[7]对220 kV电缆中间接头可能出现的半导电尖端放电进行了气隙缺陷仿真和试验研究。他们都针对可能出现的一种空气隙缺陷进行仿真及实验，并未结合实际考虑可能出现的各种缺陷，这正是这里研究的重点。

针对高压电缆终端各种常见缺陷，将应力锥和铜屏蔽层的作用考虑在内，利用有限元仿真软件依据35 kV电缆终端实物建立各种不同形状的微间隙缺陷模型[12-14]，并研究其气隙小于1 000 μm时的最大场强。利用最小二乘法将实验数据进行拟合，得到各位置最大场强随缺陷尺寸大小变化的分布曲线。

1 基于有限元分析的静电场仿真

有限元法是以变分原理和剖分插值为基础的一种数值计算方法[15]。它首先利用变分原理把需求解的边值问题转化为相应的变分问题，即泛函的极值问题，然后利用剖分插值将变分问题离散化为普通多元函数的极值问题，最终归结为一组多元的代数方程组，解之即得待求边值问题的数值解。

在静电场二维情况下[16]，在边界为c的平面域D中，电荷密度为ρ，介电常数为ε，电位φ在边界c上满足其次第一类边值条件，

即φ|c=f(s)

和泊松方程

电场能量泛函为

(1)

泛函变分为

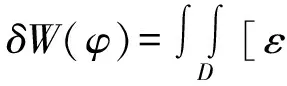
(2)

联立以上方程可得电场能量最小的条件为

δW(φ)=0

(3)

其中，δ为变分符号；E为单位场强；▽为哈密顿算符；D为积分面积。

因边界电位已知，不考虑式(3)。将定义域D剖分成有限个离散多边形子域(三角形或者四边形)，待解函数Ф在每一个单元内可以用一个合适的插值函数U(x，y)来近似[17]，设U用坐标的形函数矩阵[N]和节点势函数矩阵[φ]的线性组合来表示。

即U=[N]T·[φ]

(4)

其中

[N]T=[N1,N2,N3…,Nk,…Ns]

[φ]=[φ1,φ2,φ3…,φk,…φs]

(5)

插值函数U(xk,yk)=φk

(6)

由于部分子域电位已知，故可联立方程(4)、(5)、(6)解出插值问题的数值解。由所得电位分布，即可由方程(1)计算各子域场强大小及电场能量。

2 模型分析与建立

按照1∶1比例根据图1的35 kV电缆终端设计图建立了ANSYS有限元2维模型，相应的终端实物如图2。将模型建立后，在可能出现局部放电的半导电层断口、铜屏蔽层断口以及两者之间的半导电层区域分别模拟了割伤和凹陷两种缺陷的不同尺寸的模型，缺陷模型如图3所示。图中从上到下(Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，Ⅵ)依次为硅橡胶外套、应力锥、半导电层、电缆主绝缘层、电缆内半导电层和电缆线芯。半导电层上及铜屏蔽层断口处用三角形区域模拟割伤缺陷、等腰梯形模拟凹陷缺陷。半导电层断口处割伤、凹陷缺陷均设为三角形。

采用有限元方法对模型进行静电场仿真，可得到其电位分布，电场强度矢量和分布。不同位置的缺陷模型如表1所示。

在以上容易出现局部放电的位置分别建立等比例不同大小的缺陷模型进行仿真验证。电缆终端可能出现沿面滑闪放电缺陷、导电颗粒放电缺陷、内部气隙放电缺陷、线芯毛刺放电缺陷等故障缺陷。这些缺陷最终都是由于存在空气或者其他填充物形成微间隙，而微间隙与周围绝缘材料的介电常数不一致，从而导致电场分布不均。因此，可以通过模拟不同介电常数的填充介质的割伤缺陷和凹陷缺陷来模拟电缆终端可能出现的各种缺陷。电缆终端缺陷模型的各种材料介电常数及电导率见表2。

图1 电缆模型剖面图

表1 两种缺陷位于不同位置

说明：①、④在半导电层上，位于铜屏蔽层断口处；②、⑤在半导电层上，位于半导电层断口与铜屏蔽层断口之间；③在电缆主绝缘上，位于半导电层断口处；⑥在电缆主绝缘与应力锥之间，位于半导电层断口处。

图2 35 kV电缆终端剖面图

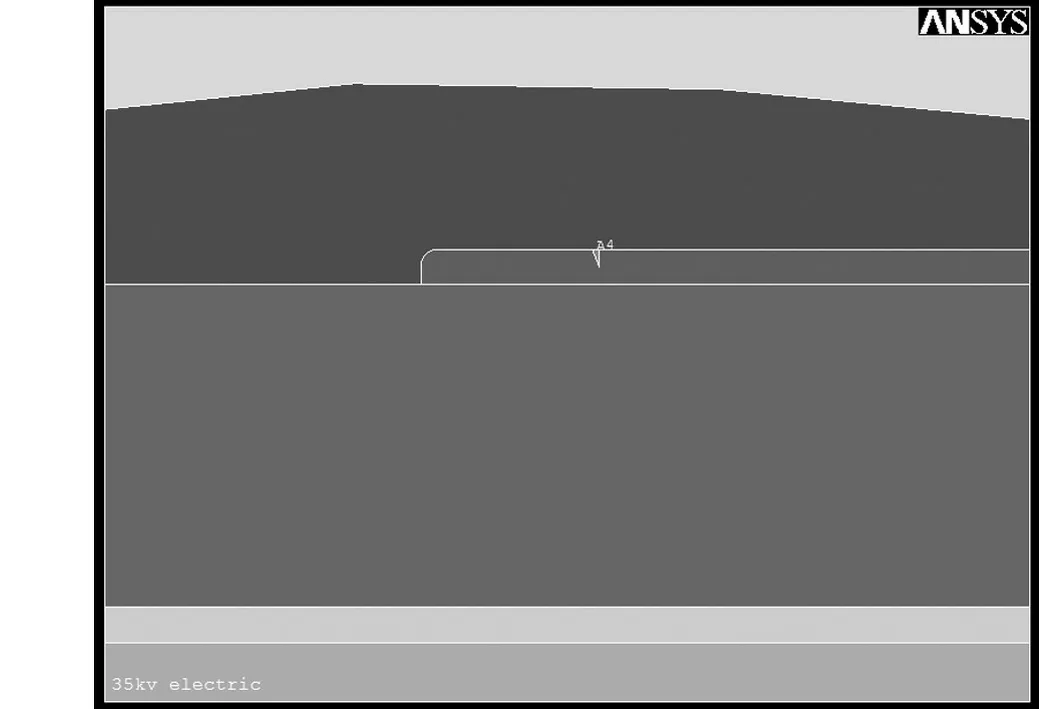
图3 模拟35 kV电缆终端割伤缺陷

表2 不同材料的相对介电常数和电导率

在仿真试验时，对电缆线芯施加35 kV电压终端外表面及铜屏蔽层施加0电位。对模型进行网格划分时，采用统一的划分并将缺陷位置处进行最大细化。

3 最小二乘法数据拟合及实验结果分析

3.1 最小二乘法拟合

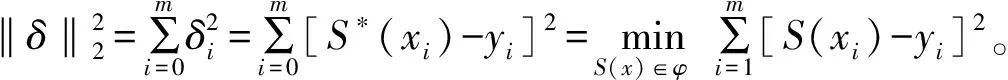
用最小二乘法求拟合曲线时，首先要确定S(x)的形式。这与所研究问题的运动规律及所得数据(xi,yi)有关；通常从问题的运动规律及给定数据描图，确定S(x)的形式，并通过实际计算选出比较好的结果。研究缺陷模型的最大场强随缺陷模型尺寸大小变化的规律，用最小二乘法可以自动筛选掉变化太大不符合规律的奇异点，构造出光滑的运动曲线，故采用此法对数据进行曲线拟合能较好反应所研究问题的变化规律。将不同缺陷模型不同大小的仿真所得场强最大值进行统计汇总，利用最小二乘法对各种缺陷所得数据进行插值和拟合。拟合步骤为：①根据数据特性，选择插值拟合函数及插值拟合次数，②根据最小二乘法曲线拟合准则编程计算拟合函数系数，③进行拟合绘图。

得到以下拟合函数。

半导电层割伤拟合函数为

y=-235.803 8x4+512.692 3x3-333.606 8x2+75.717 8x+7.669 6

半导电层凹陷拟合函数为

y=-14.187 5x2+18.457 5x-0.706 0

半导电层割伤拟合函数为

y=-235.803 8x4+512.692 3x3-333.606 8x2+75.717 8x+7.669 6

半导电层凹陷拟合函数为

y=-14.187 5x2+18.457 5x-0.706 0

铜屏蔽层断口处割伤缺陷拟合函数为

y=646.8x4-1 542.3x3+1 361x2-525.5x+100.7

铜屏蔽层断口凹陷伤缺陷拟合函数为

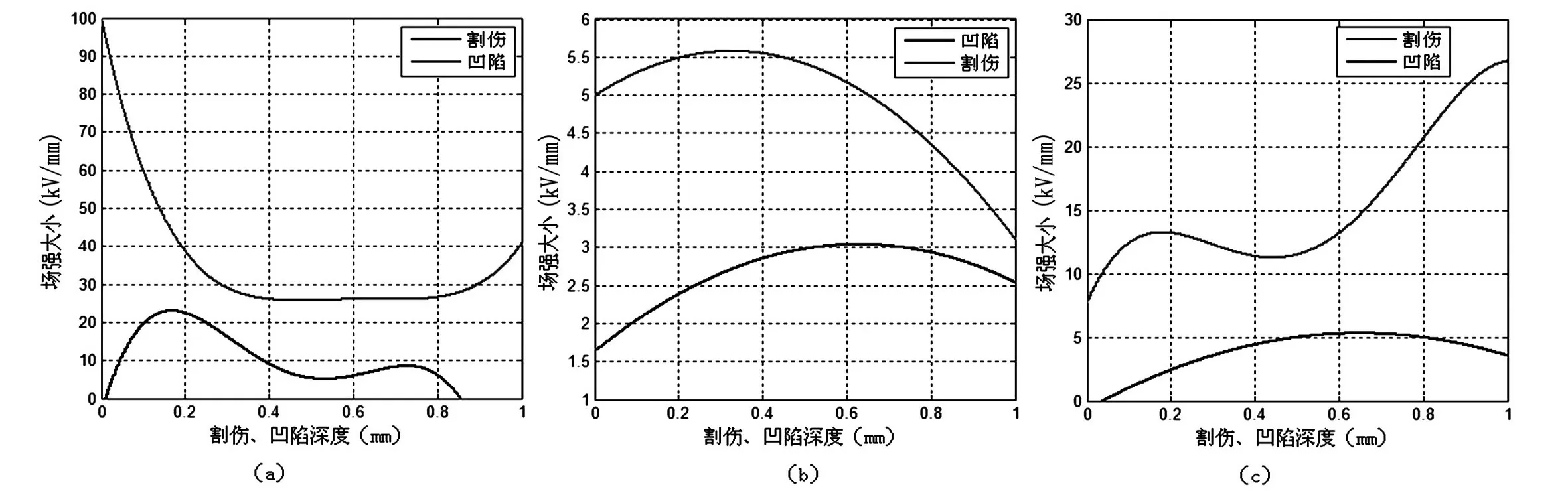
图4 各个位置割伤、凹陷缺陷最大场强拟合曲线

y=-1 480.1x4+2 822.3x3-1 779.7x2+388.4x-4.2

半导电层断口处主绝缘割伤缺陷拟合函数为

y=-3.567 8x2+4.485 7x+1.629 1

半导电层断口处凹陷缺陷拟合函数为

y=-5.45x2+3.575x+4.99

各拟合函数经最小二乘法多次拟合后绘制如图4。

3.2 实验结果分析

以往的研究，常常在建模仿真试验时忽略铜屏蔽层的存在。通过研究发现，铜屏蔽层是一个至关重要的部分，是极易发生局放的薄弱环节。铜屏蔽层的作用是，正常情况下流过电容电流，短路时作为短路电流的通道，同时也起到屏蔽电场的作用[18]。其断口处由于气隙缺陷的存在，会使接触电阻增加，限制了短路容量的大小，并且电流不是沿轴向流动，而是绕轴心成螺旋流动，引起电感，导致感应电动势增加。如图4(a)所示：铜屏蔽层断口处存在缺陷时，场强将急剧增大，平均场强远大于空气击穿场强30 kV/cm。其中割伤缺陷随割伤深度增大呈递减趋势，当间隙小于0.1 mm时，最大场强接近100 kV/mm,极易造成绝缘材料老化加剧，并产生局部放电。对于此处的凹陷缺陷，场强平均约为10 kV/mm，同样容易产生局部放电。因此，电缆终端铜屏蔽层断口处极易成为局部放电的源头，应当认真做好铜屏蔽层的直流电阻或感应电压和电流测试，及时更换老化终端，避免事故的发生。

在未考虑铜屏蔽层的终端仿真中，半导电层断口处主绝缘割伤等缺陷会有很大场强，易发生局部放电。将铜屏蔽层考虑在内时，由于铜屏蔽层对电场的屏蔽作用和应力锥的应力疏散作用，使得半导电层断口处微气隙缺陷的场强过大问题得到改善。如图4(b)所示：缺陷平均场强被控制在4.5 kV/mm以下。由于半导电层和应力锥接触良好，且有相似的介电常数，故在用有限元法进行计算时可看作一体，而电缆主绝缘较应力锥和半导电层有稍小的介电常数，使得周围介质的介电常数相对缺陷气隙差距减小。因此此类缺陷局部场强比其他缺陷小，不至于发生局部放电。

位于铜屏蔽层断口与半导电层断口之间的半导电层，由于铜屏蔽层的剥除，电场应力在铜屏蔽层断口附近集中，半导电层上的电场分布也随之改变。如图4(c)所示：实验模拟之割伤缺陷较凹陷缺陷有较大场强，且与割伤深度成正比例关系，其平均场强大于10 kV/mm，超过空气击穿最大场强，长期运行会使缺陷边缘的介质介电常数减小，由于场强与介电常数成反比例关系，故缺陷处会产生更大的场强，形成恶性循环，从而加快电缆终端的老化并最终产生局部放电。根据各类电缆终端缺陷仿真数据各类缺陷所得最大场强，对各类缺陷局部放电可能性进行预估。归纳如表3。

由以上实验数据可知，在可能产生局部放电的各处位置，割伤缺陷较凹陷缺陷有更大的场强，更容易发生局部放电。电缆终端缺陷模型越尖锐，电场畸变越严重，介质材料发生变化部位的场强越大。这与前人研究结果一致。不同的是铜屏蔽层断口处应力集中，场强过大，是电缆终端的薄弱环节，也是最容易产生局部放电的位置。半导电层断口处由于应力锥的作用，使应力得到明显疏散，从而大大降低场强，减小了局部放电的可能。因此安装电缆终端时，要注意不能割伤半导电层并将半导电层表面及各断口打磨光滑成反应力锥形状，需用硅脂以及绝缘胶等绝缘材料填充电缆半导电层表面及断口处可能存在的微间隙，防止形成微间隙缺陷，减小局部放电发生的可能性。

表3 不同缺陷局部放电可能性对比

4 实验验证

由现场实验所得发生局部放电的35 kV电缆终端实物剖析所见，与仿真所得结论相符。检查故障电缆终端，可见铜屏蔽层断口处未进行打磨和绝缘应力控制形成微气隙缺陷，且半导电层断口不齐，有台阶气隙缺陷导致局部放电。如图5所示。放电位置为铜屏蔽层断口处(白圈范围内)。

图5 铜屏蔽层断口气隙缺陷

5 结 论

用有限元法对35 kV电缆终端进行仿真试验，分析不同尺寸的割伤和凹陷缺陷的最大场强分布，结合最小二乘法将数据进行曲线拟合后对比得出以下结论。

(1)越靠近铜屏蔽层的地方，应力控制越薄弱，局部场强越大。

(2)同样的位置割伤缺陷比凹陷缺陷局部场强大，更容易产生局部放电。

(3)铜屏蔽层断口处应力集中，场强较大，易产生局部放电，是生产和安装时应注意的薄弱环节。

从现场实验所得故障终端证实了仿真所得铜屏蔽层为局部放电薄弱环节。拟合所得数据对电缆终端内部可能出现的局部放电缺陷位置定位和大小测量提供了数据支持。对电缆故障终端的绝缘电树枝老化及使用寿命有一定指导意义。通过最小二乘法曲线拟合，结合现场局部放电试验检测可以大致估计产生局部放电的位置和缺陷大小。结合所得局部部电放电量、放电次数以及放电时间间隔等数据，进行局部放电故障诊断分析、预估电缆终端老化曲线等问题有待下一步研究。

[1] 唐炬,龚宁涛,李伟,等.高压交联聚乙烯电缆附件局部放电特性分析[J].重庆大学学报，2009,32(5)：528-529.

[2] 陶诗洋,冯义,曹佳楣,等.高频传感器在10 kV电缆带电检测中的应用[J].中国电力，2011，44(3)：27-29.

[3] 王超,刘毅刚,刘刚,等.有限元法应用于电缆终端应力锥缺陷分析[J].高电压技术，2007,33(5)：152-153.

[4] 周凤争,孟庆霖，朱晓辉,等.10 kV电缆附件典型缺陷仿真与绝缘故障分析[J].绝缘材料，2011,44(4)：67-68.

[5] 唐炬,李伟,欧阳有朋.采用小波变换奇异值分解方法的局部放电模式识别,[J].高电压技术，2010,36(7):1686-1687.

[6] 刘刚,陈志娟.10 kV交联聚乙烯电缆终端主绝缘含空气气隙缺陷试验[J].高电压技术，2012,38(3):678-682.

[7] 姜芸,闵红,罗俊华.220 kV电缆接头半导电尖端缺陷的局部放电试验[J].高电压技术，2010,36(11):2657-2660.

[8] M.Pompili，R. Bartnikas.On Partial Discharge Measurement in Dielectric Liquids[J].IEEE Transactions on Dielectrics and Electrical Insulation，2012,19(5):1476-1481.

[9] Sedat Adili，Christian M. Franck.Application of Pulsed X-ray Induced Partial Discharge Measurements[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2012,19(5):1833-1839.

[10] T.Asokan，T.C. Balachandra.Electrical Discharge Behavior of Micro-gaps[J].IEEE Transactions on Dielectrics and Electrical Insulation,2011,18(6):1864-1868.

[11] H. Illias, G. Chen，P. L. Lewin.Modeling of Partial Discharge Activity in Spherical Cavities Within a Dielectric Material[J].IEEE Electrical Insulation Magazine,2011,27(1):38-45.

[12] Hazlee Illias，George Chen.Partial Discharge Behavior within a Spherical Cavity in a Solid Dielectric Material as a Function of Frequency and Amplitude of the Applied Voltage[J].IEEE Transactions on Dielectrics and Electrical Insulation,2011,18(2):432-443.

[13] H.A.Illias,G. Chen.Partial Discharge within a Spherical Cavity in a Dielectric Material as a Function of Cavity Size and Material Temperature[J].IET Science,Measurement and Technology,2012, 6(2):52-62.

[14] L. H. Germer.Electrical Breakdown between Close Electrodes in Air[J].Journal of Applied Physics,1959,30(1):46-51.

[15] 李华春,章鹿华,周作春.应用有限元方法优化应力锥设计[J].高电压技术，2005,31(11):55-58.

[16] 阎照文.工程电磁分析技术与实例详解[M].北京：中国水利水电出版社,2006.

[17] 张榴晨.有限元法在电磁计算中的应用[M].北京：中国铁道出版社,1996.

[18] 刘子玉、王惠明，电力电缆结构设计原理[M].西安：西安交通大学出版社,1995.