解析研究侧偏工况下多自由度汽车的轮胎磨损

高保恒

(山东理工大学 交通与车辆工程学院， 山东 淄博 255091)

1 轮胎磨损的解析研究

磨损量(磨耗量)又叫磨耗减量，是衡量橡胶耐磨性的主要指标.磨损量是以长度、体积、质量等单位表示的磨损物理量，是指由磨损引起的材料损失量，它可通过测量长度、体积或质量的变化而得到，并相应称它们为线磨损量、体积磨损量和质量磨损量.

1.1 磨损量的表示方法

磨损量的测定和表示方法很多.目前我国多采用阿克隆磨耗试验法.它是使橡胶(胶轮)在一定的倾斜角度(15°)和一定负荷(26.66N)作用下，与标准硬度砂轮(邵氏78度)进行摩擦，测定橡胶在一定行程(1km或1.61km)内的磨损量， 用cm3/km或cm3/1.61km来表示.此值愈小，则橡胶的耐磨性愈好.因此，轮胎的磨损量如何用解析数值的理论表征出来，在理论上就显得尤为重要.

就目前的文献研究所知[1]，表征轮胎磨损量的方法主要有：

(1)有限元法[2-3]，利用有限元的方法计算接地印迹上的力分布函数或胎面宽度方向上的接地压力之后，再借助其它可以计算磨损的公式来计算轮胎的磨损量.

(2)单位磨损里程表示法[4]，单位磨损里程是指胎面磨耗每毫米花纹沟深所行使的里程.

(3)轮胎磨损能量计算法[5-9]，轮胎与路面间的磨损需要消耗能量，因此如果能计算出轮胎的滑动损失能量，就可以得出轮胎的磨损量[9-10].

1.2 磨损量的解析表示[11]

将轮胎胎体假设为刚性、胎面为弹性的刷子模型，轮胎的接地印迹长度为l，宽度为ω，不考虑轮胎宽度变化的影响.轮胎在制动或驱动时，轮胎的摩擦损失分为如图1所示的两部分.距离接地前端为X的路面上的点与胎面底部的相对变形ΔX为

ΔX=SX

(1)

式中S为滑动率.

切向应力fX为

fX=CXSX

(2)

式中CX为橡胶块的横弹性常数.

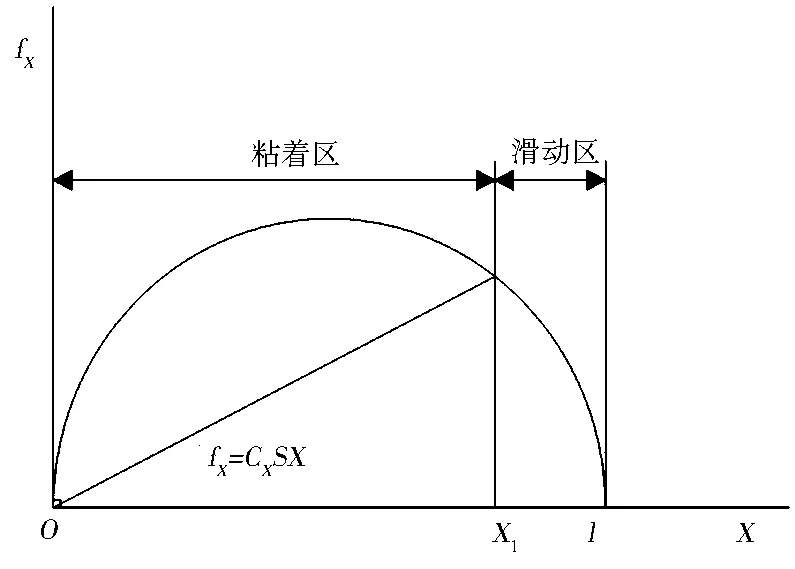
图1 轮胎的切向剪应力

轮胎开始滑动点X1为

X1=l(1-q)

(3)

在开始滑动以前，轮胎处于图1所示的粘着区域内，所以在该区域内每单位面积橡胶块所储存的变形能量为

(4)

当轮胎滑动时，在粘着区所储存的能量e1就将作为滑动能量而消耗掉.

当轮胎在滑动区时，轮胎将一直处于滑动摩擦的状态，在此期间轮胎摩擦损失的滑动能量为

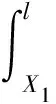
(5)

轮胎转动一个单位长度所消耗的能量为

EB=e1+e2=

(6)

在滑动率S非常小的情况下，近似的取q=0，推得

EB=KXS2

(7)

由制动、驱动以及侧偏的特性理论可知，轮胎的侧偏角的tanα就等于滑动率S，所以在公式(7)中，用tanα代替S，并且在侧偏角较小的情况下，可得到侧偏时轮胎滑动能量的损失为

EC=KYtan2α

(8)

式中KY为常数，取决于轮胎自身的结构特性.

由文献[11]知，在侧偏角较小的情况下，胎面滑动磨损量与轮胎磨擦损失能量成近似正比关系.故，轮胎的胎面滑动磨损量为

ΔH=KCEC

(9)

式中KC为常数，由橡胶材料特性与路面特性决定.

由(8)和(9)知，轮胎磨损量与侧偏角的函数关系为

ΔH=KZtan2α

(10)

式中KZ=KCKY.

2 多自由度整车的实际行驶特性

2.1 建立9自由度的整车模型

该整车模型的自由度分别为：沿前进方向的自由度；侧向方向的自由度；角自由度ωr；前转向轮的转角自由度；左前轮、右前轮、左后轮、右后轮的旋转运动自由度.为了得到一些特定的特性，我们在分析中采用以下一些原则：

(1)忽略转向系统的影响，直接以前轮转角作为输入.

(2)在本文条件下，汽车沿x轴的前进速度u保持不变.

(3)汽车的侧向加速度限定在0.4g以下，轮胎侧偏特性处于线性范围.

(4)作用于汽车上的驱动力不大，不考虑地面切向力对轮胎侧偏特性的影响，没有空气动力的作用.

(5)忽略左右车轮轮胎由于载荷的变化而引起的轮胎特性的变化及轮胎回正力矩的作用.

这样，实际上汽车便简化成仅有9个自由度的整车模型，如图2所示.它是一个由前、后四个有侧向弹性的轮胎支撑于地面、具有侧向及横摆运动的9自由度的整车模型.

图2 9自由度的整车模型

分析时，令车辆坐标系的原点与汽车质心重合.

显然，汽车的质量分布参数，如转动惯量等，对固结于汽车的这一动坐标系而言为常数，这正是采用车辆坐标系的方便之处.

2.2 实际行驶状态下的轮胎侧偏角

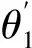
(11)

(12)

前、后车轮的侧偏角：

(13)

α2=θO-η2

(14)

(15)

(16)

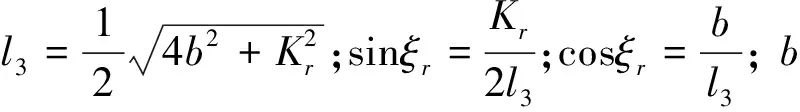
2.3 整车的实际行驶特性

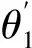
(17)

式中：K为主销中心距；m为梯形臂长；λ为梯形底角.

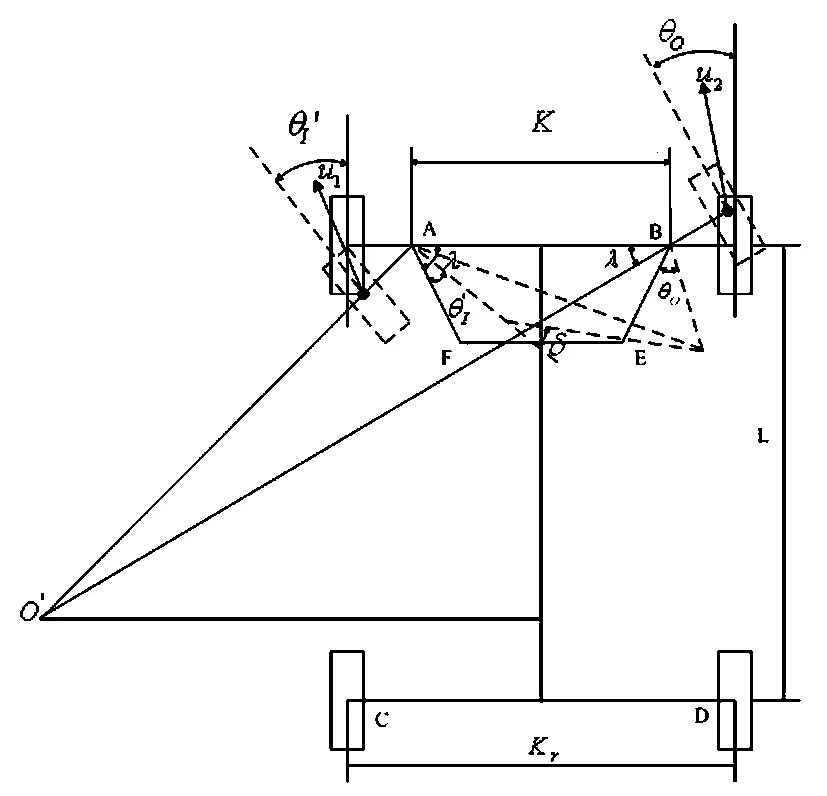
图3 实际的内、外轮转角关系

3 轮胎磨损的解析表达式

联立公式(10)及(11)、(12)(13)、(14)、(15)、(16)得到处于侧偏状态下各轮胎磨损量的解析公式：

(18)

(19)

(20)

(21)

4 结束语

1)从公式(18)、(19)及(17)中可知，转向梯形的结构参数与轮胎的磨损存在着必然的非线性关系，究竟这两者存在什么样的非线性关系，有待进行进一步的研究.

2)从公式(20)、(21)中可知，汽车两后轮的磨损与汽车的行驶状态、行驶速度以及底盘结构有较大关系.同时，当汽车只做单侧转向运动时，其后轴内侧轮胎的磨损量要大于同轴外侧轮胎的磨损量.

轮胎自身的结构和材料特性、道路的路面特性以及汽车的行驶状态对轮胎造成的磨损是无法彻底消除和避免的，但是通过对汽车转向梯形结构参数优化能更好地减少轮胎磨损，使汽车获得更理想的转向特性.

[1] 黄海波, 勒晓雄, 丁玉兰. 轮胎偏磨损机理及数值解析方法研究[J]. 同济大学学报：自然科学版, 2006, 34(2): 234-238.

[2] 沈浩. 轮胎偏磨损机理及动力学改进方案研究[D]. 上海: 同济大学，2000.

[3] 方庆红,路金林, 赵立群,等. 轮胎磨损分析中接地能量损失的有限元计算模型研究[J]. 沈阳化工学院学报, 2002, 9(3): 227-229.

[4] 李文辉,魏宏,吴光强.轮胎磨损解析研究[J].汽车技术, 2002(6):13-15.

[5] 庄继德. 现代汽车轮胎技术[M]. 北京:北京理工大学出版社, 2001.

[6] Knisley S. A correlation between rolling tire contact friction energy and indoor tread wear[J].Tire sciences and technology,2002,20(2):83-84.

[7] Lupker H. Numerical prediction of car tire wears phenomena and comparison of the obtained results with full-scale experimental tests[R]. Helmond: Chassis and Transport Systems Department, TNO Automotive, 2003.

[8]Lupker H. Tire and road wear prediction[R]. Helmond: Chassis and Transport Systems Department, TNO Automotive,2003.

[9] Zhang S W, Yang Z C. Energy theory of rubber abrasion by a line contact[J]. Tribology International, 1997, 12(30):836-839.

[10]Bui Q V, Ponthot J P. Estimation of rubber sliding friction from asperity interaction modeling[J]. Wear, 2002(252):149-151.

[11] 庄继德.汽车轮胎学[M]. 北京:北京理工大学出版社, 1995.