基于非递归结构的多级余弦CIC滤波器

李功福，石 玉，赵宝林

(电子科技大学微电子与固体电子学院，四川成都 610054)

数字滤波是移动通信和无线网络中的重要部件，能满足滤波器对相位及幅度的要求又能避免模拟滤波器带来非线性失真和电压漂移等问题，故数字滤波器日趋重要。其按单位冲击脉冲响应长度分为有限与无限脉冲响应(Finite Impulse Response，FIR;Infinite Impulse Response，IIR)两类。CIC抽取滤波器是FIR的一种，它由积分滤波器、抽取因子、梳妆滤波器3部分构成，利用抽取因子可实现数字上下变频，但其选择性性能较差，是目前的主要研究方向。文中利用余弦滤波器较好的滚降特性来提高CIC抽取滤波器的选择性，加上非递归结构使其便于工程实现。

1 CIC原理及仿真

CIC滤波器结构，如图1所示。

图1中由于其实现不需要乘法器、存储器，而被广泛应用于各变采样率系统中，一般用在抽取滤波器的第一级或插值滤波器的最后一级。图1中前部分为积分滤波器，工作在高采样率Fs下，它属于单极点IIR滤波器，非稳定系统。单级传递函数为

状态方程为

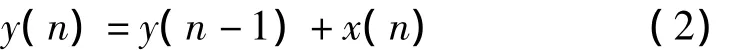
图1 级连CIC抽取滤波器

图1中后部分为梳妆滤波器，工作在低采样率Fs/M下，其单级传递函数为

状态方程为

其中，D为每级微分器延时D个样本，工程中一般取值1或2，M为抽取因子。

由式(1)、式(3)可得到单级CIC抽取滤波器的传递函数为

式(5)所示，H(z)有M个零点和1个极点，零点在2π/DM处，而极点在Z=1处，这恰好与零点抵消。

一级CIC滤波器的幅频响应如图2所示，M=2，M=4，M=6，M=8，D=1。从图中可看出其为低通滤波器，但其选通性和寄生通带抑制较差，且阻带压制不够，不能在实际中应用。

图2 一级CIC的幅频响应

2 多级余弦CIC抽取滤波器

软件无线电中，A/D后的信号要大比率抽取，即M较大，对M进行分级处理

余弦滤波器也是一种无乘法器的滤波器，它能对数字信号进行成形滤波、压缩旁瓣、减少干扰等影响。其传递函数为

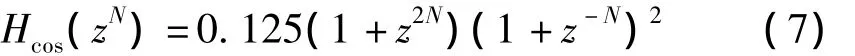
通过上式可知:(1)非递归结构的余弦滤波器比CIC滤波器形式简单，且易采用流水硬件结构。(2)系数0.125为单位直流增益。

多级余弦CIC滤波器的传递函数便为

其中取值一般为Ni=M/2i+1，Nk=M1。例如，进行32倍抽取，则有 M=32，分3级抽取则有 M=M1M2M3=8 ×2 ×2。N1=8，N2=4，N3=2。

故其级联系统的传递函数为

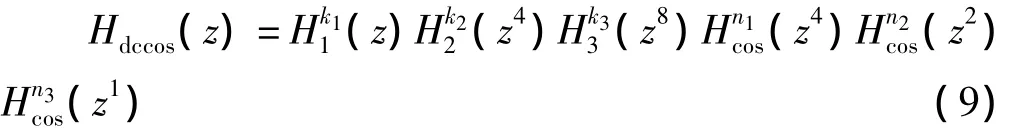
进一步优化，使其有利于硬件实现，可对CIC抽取滤波器改为递归结构。抽取因子M=2j，则CIC传递函数为

由式(10)便可得出非递归形式的CIC，如图3所示。

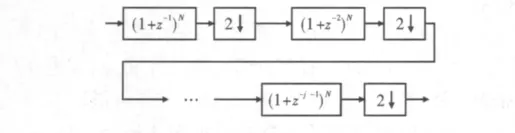
图3 非递归CIC滤波器

由式(9)和式(10)便可得到简化的其传递函数为

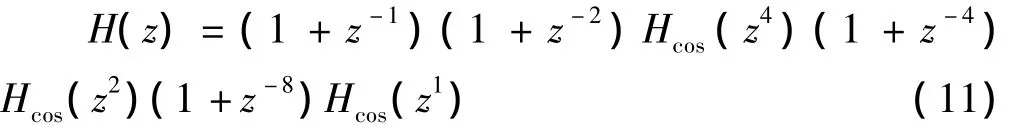
抽取因子为32，分3 级 M1=8，M2=2，M3=2，3 级余弦滤波器级数 N1=8，N2=4，N3=2。

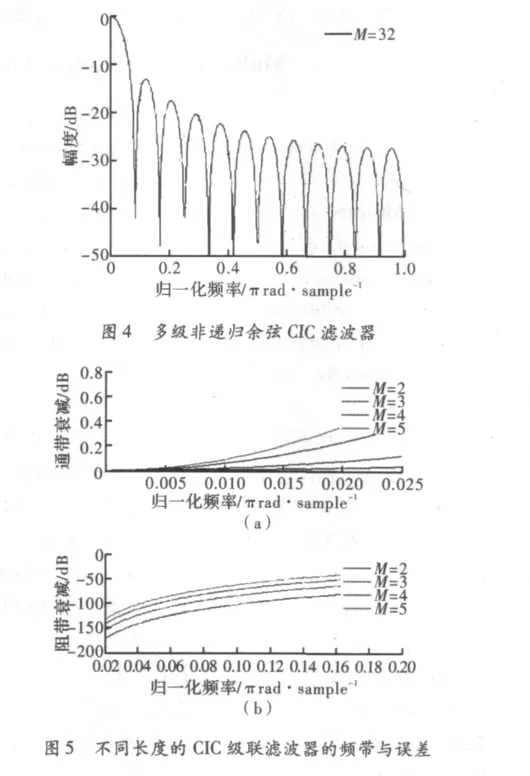
如图4所示，改进的CIC滤波器对旁瓣压制到34 dB，通带也相对平坦，其频率响应与之前有较好的改善。如图5所示，改进型低通选择性与阻带压制效果相对于传统的CIC结构滤波器有了较好的改善，已能应用于实际工程中。

3 结束语

传统的CIC滤波器结构简单、速度变换快、便于硬件实现，是数字上下变频的重要部分。又因其通带平坦度不佳、阻带抑制不够等制约了它的应用。文中就传统CIC滤波器的缺陷作分析与改进，利用余弦滤波器优良的滚降性能来提高CIC滤波器的阻带压制和通带平坦化，实验仿真结果与公式推导结果相近，使该方法得以证明。多级余弦滤波器与CIC滤波器级联并采用非递归结构使其较传统CIC滤波器在选通性上有理想的改善，系统更加稳定且也便利于硬件实现。

［1］宋寿鹏.数字滤波器设计及工程应用［M］.镇江:江苏大学出版社，2009.

［2］杜勇，路建功，李元洲.数字滤波器的Matlab与FPGA实现［M］.北京:电子工业出版社，2012.

［3］刘秉坤，王华，陈岚.高性能升余弦滤波器设计［J］.电讯技术，2006(4):61－64.

［4］刘睿强.一种升余弦成形滤波器的设计［J］.现代电子技术，2006(13):51－52.

［5］凌云志.基于DSP实现根升余弦滤波器的研究［J］.国外电子测量技术，2006，25(1):11 －13.