基于贪婪算法的太阳能小屋光伏电池组合分析

刘月华，吕永标，雷春霞，王义康

(中国计量学院理学院，浙江杭州 310018)

在设计太阳能小屋时，需在建筑物外表面铺设光伏电池，光伏电池组件所产生的直流电需要经过逆变器转换成220 V交流电才能供家庭使用，并将剩余电量输入电网。不同种类的光伏电池每峰瓦的价格差别较大，且每峰瓦的实际发电效率或发电量受诸多因素的影响，如太阳辐射强度、光线入射角、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及架设方式等。因此，在太阳能小屋的设计中，研究光伏电池在小屋外表面的优化铺设，是目前太阳能在农居工程中的研究热点之一。

对于特定规格的小屋，当其所在地区的光照强度、电池板和逆变器的参数价格、光照面积等因素确定的情况下，可以利用相关优化算法求解出电池组件的最优铺设方案。本文基于贪婪算法的思想，根据文献［1］给出的相关背景研究小屋外表面光伏电池的优化铺设问题，选出电池组件分组数量和容量，以及相应数量和容量的逆变器，为太阳能小屋的优化设计提供参考。

1 电池板最佳倾角的计算分析

光伏电池板安装的倾角、朝向均会影响其接收太阳能辐射量。利用直接辐射量的样本数据，通过Hay天空散射各向异性模型［2］，可以计算出安装有倾角朝向的电池板接收到的实际辐射量。电池板方位和朝向示意图，如图1所示。

根据各向异性模型的推导和计算，得到各变量之间的关系式为

图1 电池板方位角和倾角示意图

式(1)中，HT为倾斜面上的太阳总辐射强度;Hz为水平面上的太阳总辐射强度;HB为法向直接辐射强度;HD为水平面散射辐射强度;H0为大气层外水平辐照量，一般取H0=1 367 W/m2;RB为倾斜面和水平面上直接辐射量的比值;ρ表示地物表面反射率，其范围一般为10% ～35%，文中在计算时取ρ=20%;β为太阳能小屋屋顶斜面倾角;式(2)中θr太阳光入射角，即太阳辐射光线与屋顶表面的夹角;θz太阳天顶角，与太阳高度角α互余。

由太阳能相关理论知识及概念［3］可知

其中，φ为纬度(本文以山西大同地区为研究对象，取40.1°);n为日期序号;w为时角;ts为太阳时;A为太阳方位角;γ为斜面方位角，表示太阳光线的水平投影偏离正南方向的角度，取正南方向为起始点，向西(顺时针)为正，向东为负。

结合文献［1］所给的小屋外观，设东立面、西立面、南立面、北立面、偏南屋顶和偏北屋顶的斜面方位角分别为 γ东= － 90°，γ西=90°，γ南=0°，γ北=180°，γ1=0°，γ2=180°。由式(1)～ 式(8)，把方位角 γ 分别代入，求得东立面、西立面、南立面、北立面、偏南屋顶和偏北屋顶的最佳倾斜角，即使得每个面的年平均辐射强度最大的倾角，分别为 β东=0°，β西=28°，β南=12°，β北=0°，β1=12°，β2=0°。

2 贪婪算法的基本思想

贪婪算法［4］(Greedy Algorithm)是一种对某些求最优解问题的更简单、更迅速的设计技术。它的基本思想是以当前情况为基础根据某个优化测度作最优选择，而不考虑各种可能的整体情况，省去了为找最优解要穷尽所有可能而耗费的大量时间，通常采用自顶向下，以迭代的方法做出相继的贪心选择，每作一次贪心选择就将所求问题简化为一个规模更小的子问题，通过每一步贪心选择，可得到问题的最优解，虽然每一步都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的。

贪婪算法是通过一系列选择步骤来构造问题的解，每一步都是对当前部分解的一个扩展，直至获得问题的完整解。所做的每一步选择都必须满足:(1)可行性。必须满足问题的约束。(2)局部最优。当前所有可能的选择中最佳的局部选择。(3)不可取消。选择一旦作出，在以后的步骤中无法改变。

使用贪婪算法解决问题，通常需要明确问题的求解目标，分析问题所包含的约束条件，建立优化函数以及制定贪婪准则。

3 电池优化组合分析

3.1 电池和逆变器的组合优化分析

光伏电池组件分组和逆变器的选择配置须遵循一定的技术要求［1］，在进行电池优化组合的过程中，不仅要考虑到发电量尽可能大、单位发电量费用尽可能小，还要满足光伏电池组件阵列的连接要求和逆变器的选配要求。在限定铺设面积的情况下，对电池组件和逆变器的优化组合配置，这是一个NP难问题。本文采用贪婪算法，先进行光伏电池的优化组合，找到每个立面的组件阵列问题的局部最优解，然后针对每个立面选定的电池阵列进行逆变器的选配。

在已知电池价格计算标准的基础上，设电池的市场价格为p;每峰瓦的价格为g;组件功率为l，可得

又因为电池板的发电量等于接收到太阳辐射功率与转换效率的乘积，设电池板每年接收到的辐射功率为H;发电转换效率为η;每年的发电量为s，则

根据文献［1］中的电池组件设计参数和市场价格分析，不同电池的发电量不同，其价格也不同，同时电池的转换效率也会随着使用年数的增加而衰减，对每块电池35年内的效益进行计算，设为y，则

以南立面为例，对调查采集得到的24种型号［1］电池的效益和35年内的发电量进行计算，得到具体数据如表1所示。

表1 24种电池在35年内的效益和发电量

如表1所示，以电池寿命35年计算，其中A1、A2、A4、A5、A6的效益为负值，即在南面使用这些电池会亏损。这是因为南面的太阳辐射强度不够强，虽然这些电池的转化率和年发电量都很高，但是其价格也较高，导致它们的作用不能被充分利用，而造成资源浪费，不能在寿命期内回收投资，所以在辐射强度弱的墙面可以考虑多安装转化率较低，价格相对便宜的电池。

由表1可得各类型电池的效益优度排序，利用贪婪算法，效益越大的电池优先选入，在进行铺设排列设计时，进行优化组合。再根据附件所给光伏电池组件的分组及逆变器配置的要求［1］，基于贪婪算法进行逆变器的合理选择，具体流程如图2所示。

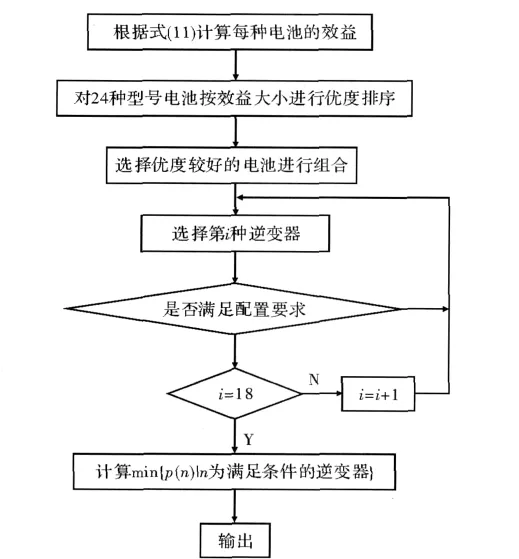
图2 基于贪婪算法求解电池组合设计问题的流程图

这种方法对问题进行了一定程度的简化以便于实现求解，但是求解得到的最优电池阵列及针对该阵列选出的合理逆变器，这样的组合是局部最优的。为更精确地寻求最优解，针对电池排列和逆变器的选择的组合问题的求解，引入模块化概念，把电池和逆变器的选择绑定，建立多目标规划模型进行求解，再结合贪婪算法基于多步优化算法寻找最优模块。

3.2 电池和逆变器的组合求解

根据光伏电池组件分组阵列连接和逆变器选配要求，可以得到选择电池阵列和逆变器时需要满足的限制条件，本文的目的就是要在满足这些限制条件的电池阵列中，进行优化选择布局铺设小屋的部分外表面，使得小屋的全年太阳能光伏发电总量尽可能大，而单位发电量的费用尽可能小［5］。考虑到电池阵列和逆变器的选择紧密相关，所以在优化布局时电池阵列和逆变器的选取是同步进行的，将满足限制条件的总体称为“可行模块”。对于这个问题，可以通过建立多目标规划模型，来寻找“可行模块”中的“优化模块”。

由于只有同种型号的电池才能串联，所以在一个逆变器连接的分组阵列里，设第i种电池的串联有ai个支路(i=1，2，…，24);第i种串联电池的第j个支路有 bij个电池串联(i=1，2，…，24，j=1，2，…，ai);ai为第i种电池的年发电量;pi为第i种电池的价格;mi为第i种电池的面积;z为产出率(分组阵列在35年内的单位面积效益值);μk为第k种逆变器的转换效率;则有［6］:

目标函数1 小屋的全年太阳能光伏发电总量尽可能大

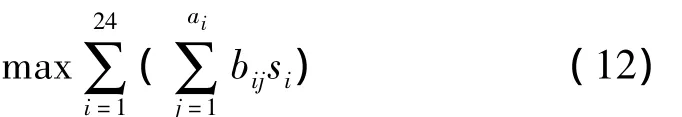
目标函数2 单位发电量的费用尽可能小

对于目标函数1和2，引入“成本—效益”概念，以购买电池和逆变器的费用为投入，电池阵列发电获取的费用为产出。设定“产出率”指标来衡量“可行模块”的优劣，建立以产出率为目标函数的规划模型，等效上述多目标规划来寻找“优化模块”。

根据上述分析，以产出率为目标函数来寻找所有可行模块中的优化模块来构建多目标规划模型。

(1)目标函数

即

(2)约束条件［1］

1)并联的光伏组件端电压相差不应超过10%。要满足并联的所有光伏组件端电压相差都不超过10%，则所有支路的最大电压和最小电压之间满足条件即可。设第i种电池的开路电压为vi，即可得并联电压约束

2)光伏分组阵列的端电压应满足逆变器直流输入电压范围。光伏阵列中所有支路的电压均要满足逆变器直流输入电压范围，设第k种逆变器的电压范围为［Vxk，Vdk］;则应满足电压范围约束

3)光伏阵列的最大功率不能超过逆变器的额定容量。根据电池组件选逆变器或者根据逆变器设计电池阵列，都要满足阵列的最大总功率不能超过逆变器的额定容量。设第i种电池的组件功率为li，第k种逆变器的功率容量为lk，则应满足最大功率约束条件

4)铺设尺寸大小的约束。在对给定小屋部分外表面进行铺设的实际计算中，结合小屋外观尺寸图，由于每个面的形状、大小和辐射量都有较大差别，所以每个面的铺设情况也不尽相同。设第i种电池的长为qi，第i种电池的宽为ci，立面可铺设的长度和宽度分别为A、C，则增加尺寸的约束条件为

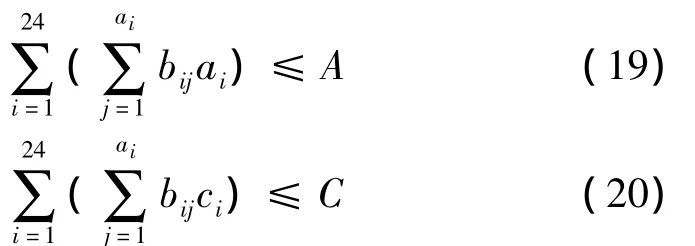
式(14)～式(20)构成寻找优化模块的多目标整数规划模型，对此模型进行求解，即可得到小屋各立面光伏电池铺设的组合优化设计方案。

3.3 模型的求解

上述规划模型难于直接求得最优解。只能通过“定一求一”的思想来进行求解，即固定逆变器的型号，基于上述模型的规划借助Lingo软件工具求解出最优电池阵列。这样在每个面中，可得对应于每个逆变器的电池阵列排列和连接方式，遍历求解每种逆变器形成18个“优化模块”，同时可得此“优化模块”的“产出率”。结合贪婪算法思想，通过比较“产出率”的大小，找到产出率较大的优化模块即为此立面的优化铺设方案。求解的具体步骤为:

Step1从南立面开始设计电池阵列，之后依次设计北面、东面、西面、偏南屋顶、偏北屋顶，把该立面的实际可铺设的长度A和宽度C代入规划模型。

Step2针对该立面，基于规划模型遍历18种逆变器进行求解。

Step3得到该立面每种逆变器相应的“优化模块”，以及每种逆变器求解对应“优化模块”的“产出率”。

Step4比较每个“优化模块”产出率的大小，找到产出率最大的“较优模块”对应的逆变器，则此逆变器以及“较优模块”即为该立面设计的电池阵列和选取的逆变器。

Step5求解得到最终的结果之后，返回Step1，继续计算设计下一立面的“较优模块”。

基于以上模型和具体算法，以南立面为例，可以求得南面需要9个A3电池并联，并选配逆变器4，分组阵列的具体铺设如图3所示。其它几面采用类似方法可得到相应结果。

图3 小屋南立面电池分组阵列优化设计图

4 结束语

研究了太阳能小屋的外表面的铺设问题，在计算得出最优倾角的基础上，构建成本效益多目标优化模型。基于贪婪算法的思想，采用成本效益多目标优化方法，得出在最优倾角的架空条件下，太阳能电池板的优化铺设方案，较大程度上提高了光伏电池的工作效率。由于晶硅电池成本较高，实现非晶硅薄膜电池的推广与太阳能光伏建筑一体化是必要的。

［1］2012高教社杯全国大学生数学建模竞赛B题［BE/OL］.(2012－09－07)［2012－11－10］.http://www.mcm.edu.cn/problem/2012/2012.html

［2］廖华，张跃，刘祖明.光伏方阵的倾角研究［J］.云南师范大学学报，1995.15(1):43－47.

［3］于军胜.太阳能应用技术［M］.成都:电子科技大学出版社，2012.

［4］杨克昌.计算机常用算法与程序设计案例教程［M］.北京:清华大学出版社，2011.