基于系统动力学的雏菊世界模型气候控制敏感性分析

陈海滨，唐海萍

(1.地表过程与资源生态国家重点实验室，北京 100875;2.西北农林科技大学经济管理学院，杨凌 712100;3.北京师范大学资源学院，北京 100875)

英国大气物理学家J.E.Lovelock于20世纪60年代受NASA邀请，帮助寻找火星上的生命痕迹。在任务完成之后，他继续思考生命维持所必需的条件:如地球表面的温度经历了36亿年后仍然保持相对不变，而同一时期的太阳温度却升高了25%;地球是如何能够使大气中氧气浓度保持在21%左右，这个值是他认为的生命安全上限。Lovelock认为解决这样的问题需要采用一个系统的观点，而不能由生物化学或生物地球化学等学科来解答，也不能由新达尔文主义生物学来解答，答案来自于生理学或控制论［1］。

Lovelock对于Walter Cannon描述的有关产生体内平衡的协同生理过程印象深刻。Cannon认为，生命体努力维持其内部环境恒定不变［2］。Lovelock相信地球也遵循着Cannon的原理:岩石、草、鸟类、海洋和大气都齐力协力，像一个巨型的有机体一样运行来调控生存条件［3］。地球这个“超级生命有机体”需要一个名字。Lovelock的邻居，诺贝尔文学奖获得者William Golding，推荐以古希腊大地女神命名，称之为盖娅［1］。

提出伊始，盖娅假说的“超级生命有机体”这样略带神秘的概念遭到了科学保守主义者，尤其是新达尔文主义者的强烈批评，认为它是伪科学，是目的论。例如，Richard Dawkins认为，“盖娅不能产生于达尔文式的生命进化，地球作为物理实体不是自然选择的单元”［4］。为了反击对盖娅假说的批评，Lovelock于1983年提出了雏菊世界模型［5-6］。Lovelock用简单的微分方程就揭示了，假想的世界不需要一个清晰的、公认的、可以描述其内部相互作用的数学方程就可以拥有自我平衡的性质。

在雏菊世界模型中，Lovelock论证了光照强度不断增强时星球温度的变化情况。本文在此基础上，尝试用系统动力学方法进一步分析雏菊世界的气候条件对于不同初始面积分配、不同反射率组合条件的敏感性。一方面可以验证盖娅假说，另一方面通过探讨模型存在的不足，为下一步的模型改善以及盖娅假说的发展提供一些参考。

1 方法原理

1.1 盖娅假说

Lenton和Wilkinson认为，盖娅假说的发展经历了经典的3个阶段:一是“它明显是错误的”;二是“它可能有些是正确的”;三是“我们都知道它是正确的”［7］。

第一阶段 盖娅假说认为，地球有机体能调节地球系统的物理、化学成分，以使星球成为生命最优的栖息地［1，3］。这个阶段的盖娅假说是目的论的，因为他没有提出一个机制来解释，个体生物之间似乎需要某种秘密的共识来达成行星水平的环境自我调节［8］。Lovelock在其后来的文献中也承认:“20世纪70年代引入的盖娅假说认为，地球的大气、海洋、气候和地壳是由生物调节处于稳定状态，并适合于生物生存。特别地，盖娅假说认为岩石和水的温度、氧化状态、酸性和其他某些方面在任何时候都保持恒定，这个自我平衡状态是由地球表面的有机体维持的。应该认识到，盖娅假说如此阐述是错误的”［9］。

第二阶段 为了应对批评，Lovelock引入雏菊世界模型。模型的模拟结果表明，虽然太阳辐射增强了近两倍，但是行星表面温度却能够维持在雏菊生长最优温度的几度范围之内。行星水平的温度自我调节可以产生于假定的生物个体水平的温度-增长率关系，盖娅假说不是目的论［5-6］。但是，这仍然无法令进化生物学家满意。

第三阶段 这阶段的盖娅假说在批评与证明中不断完善，新版本的盖娅假说定义为“地球系统的物理、化学和生物组成部分可以调节星球，以维持其作为生命的栖息地”［9］。生命有机体对气候系统有重要影响已经不再有争议［10-11］。Lenton在Nature上发文指出:“物理系统是稳定的，生物系统可不断自我增殖，因此存在一个生物生长的物理最优状态;行星自我调节的反馈机制产生于生物体的自然选择”［12］。而进化生物学家也承认盖娅假说值得严肃思考，因为它可以解释很多重大问题［13-16］。

当然，争议依然存在。主要原因在于复杂多变的地球系统充满了不确定性，有很多案例并不支持生物自我调节地球环境的观点［17］。Lovelock在《盖娅的复仇》一书中引用William Hamilton的话说:“正如哥白尼的发现需要牛顿来解释一样，我们也需要另一个牛顿来解释为什么达尔文的自然选择会导致一个宜居的星球”［18］。无论如何，盖娅假说改变了科学界对自然、地球的观点，并推动了地球系统科学的发展。通过对盖娅假说的争论，促进了地质学、大气物理学、气象学、生物学等相关学科的发展，同时也促进了多学科的交叉、融合。

1.2 雏菊世界模型

为了证明盖娅假说，Lovelock提出了一个雏菊世界的寓言。雏菊世界是一个假想的世界，它围绕着一颗辐射能量缓慢增大的恒星做轨道运动，它意图模拟太阳-地球系统。在1983年版的雏菊世界中，只种植着两种雏菊以代表生命形式——白雏菊和黑雏菊。白雏菊和黑雏菊通过反射较多和较少太阳光，改变着各自的局地温度，后者反过来又决定了雏菊的增长率。该模型经过模拟，追踪了当太阳辐射缓慢增强时两种雏菊的种群动态以及雏菊世界的温度变化。结果证明，在太阳辐射变化的相当大范围内(从当前辐射水平的0.6倍到1.1倍)，雏菊世界的温度保持几乎恒定［5-6］。在后来的雏菊世界模拟中，加入兔子、狐狸和其他物种。结果表明，物种数量越多，整个行星的稳定性越强;也就是说，温度调节能力越强;甚至当行星受到干扰时，系统也可以保持强健和稳定［19］。这些发现都支持了生物多样性与地球系统稳定性存在正向关系的观点。

雏菊世界模型的优点在于它对纷繁复杂的地球系统的简化，使其成为回答“生物与环境相互作用会怎样”这类问题的杰出模型［20］。虽然它无法解释地球内部是如何自组织的，但是它却提供了地球系统中生物与环境紧密耦合的一般经验。在雏菊世界模型出现以后的近30年时间里，很多文献努力通过模型的演变来证明或反对盖娅假说［21］。进化生物学家通过引入特殊的案例来证明在真实的世界里面有些物种在干扰或破坏自我调节作用;而支持者通过引入其他案例证明地球自我调节作用的强健与稳定;当然也有很多理论研究关注的是自我调节实现与否的关键条件是什么。

当前，雏菊世界模型已经扩展到众多学科领域，包括非线性动态、生态系统与食物网、进化论、生理学、最大熵产生以及人造生命等。虽然仍然与盖娅理论紧密相关，但雏菊世界模型已经发展成为一个独立的模型［21］。因此，在讨论雏菊世界模型与盖娅假说的关系之外，该模型也可以用于发展整合人类活动的地球系统模型的研究。

1.3 系统动力学与Stella软件概述

系统动力学是20世纪50年代末由美国麻省理工学院教授福雷斯特(J.W.Forrester)提出［22-23］。它是一种分析研究复杂反馈系统动态行为的科学方法，是系统科学的一个分支，也是一门沟通自然科学和社会科学领域的横向学科，实质上就是分析研究复杂反馈大系统的计算仿真方法。目前，它已经广泛应用于工业、经济、生态、环境等诸多学科领域［24］。

生态系统也是一个复杂的动态系统，因此，许多生态学者认为应用系统动力学进行生态学研究将有极大潜力，并积极开展了种群数量动态、大气组成变化、土地利用与土地覆盖变化等方面的推广应用工作，各类生态系统动力学模型应运而生。

Stella软件是美国Isee公司于是1985年开发的系统模拟工具。因其图形界面十分友好，在国外已成为一个构造系统模型和模拟复杂系统动态相互关系的良好工具，被广泛应用于科研、教学、管理等诸多研究领域［25］。

2 模型假设与参数设定

2.1 模型假设

关于生物与环境条件的相互作用，雏菊世界模型假设:

(1)生物影响环境条件 如上所述，由黑、白雏菊、裸地分布的星球影响了光的吸收率，因此影响了黑、白雏菊的局地温度和星球的温度。

(2)环境条件反作用于生物 局地温度影响雏菊生长的速率。当局地温度接近于最适温度时，雏菊增长率最高;但是，如果局地温度太高或太低，雏菊覆盖的区域就会随时间减少。黑、白雏菊的年增长率与局地温度的关系表示为(1)式(图1)。

式中，R为年增长率，T为雏菊局地温度。

图1 黑、白雏菊年增长率-温度关系图Fig.1 Annual growth rate-temperature relationship of black and white daisy

2.2 参数设定

(1)星球总表面积为1000英亩;

(2)雏菊衰败速率为30%/a;

(3)为了简化模拟，假设到达地面的太阳辐射值恒定，为太阳常数值的70%，约等于947.1W/m2;

(4)星球的反射率为:

式中，A为星球反射率;αb为黑雏菊所占面积比例，Ab为黑雏菊反射率;αg为裸地所占面积比例，Ag为裸地反射率;αw为白雏菊所占面积比例，Aw为白雏菊反射率。

(5)星球整体的太阳光吸收率:

(6)太阳光吸收率与星球平均温度之间的关系用下式表达:

式中，σ =5.67 ×10－8W m－2K－4，Te为星球平均温度;SL为到达地面的太阳辐射;A为星球平均反射率。其关系如图2所示。

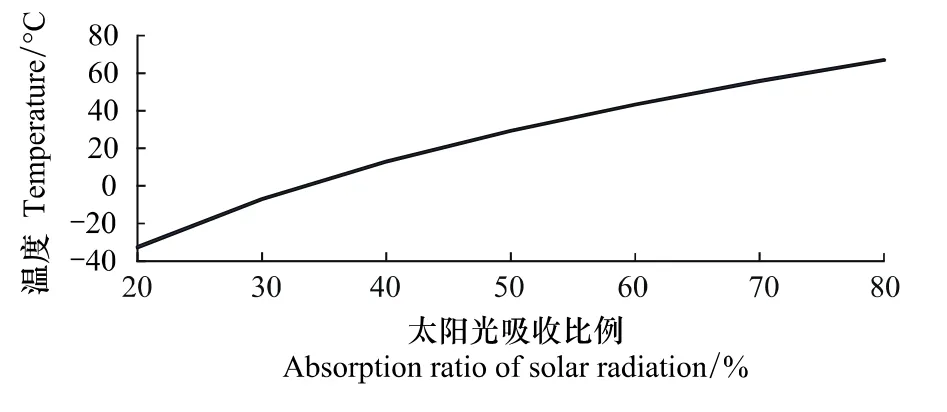
图2 星球平均温度-太阳光吸收比率关系图Fig.2 Planet's average temperature-sunlight absorption ratio relationship

(7)由于太阳光吸收率的不同，导致黑雏菊局部升温，而白雏菊局部降温:

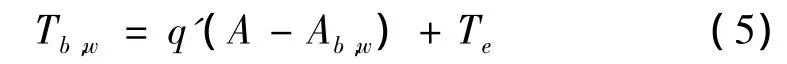
式中，Tb，w表示黑雏菊或白雏菊的局地温度;A为星球平均反射率;Ab，w表示黑雏菊或白雏菊的反射率;Te表示星球的平均温度。

根据Lovelock的模型，q′的大小表示较高温度区域向较低温度区域的热能传导能力，在这里q′取20℃。

(8)星球的裸地面积对于雏菊的现实增长率有限制作用，以增长率衰减乘数来表示这个限制作用:

增长率衰减乘数=裸地面积/星球总面积

2.3 雏菊世界因果回路图

根据上述模型假设与参数关系，绘出雏菊世界因果回路图。图3中共有8个反馈回路，白雏菊由其中4个反馈回路组合控制，黑雏菊由另外4个反馈回路组合控制。

白雏菊的4个反馈回路分别是与分布面积有关的2个正、负反馈回路;另外白雏菊的增长率受剩余空地面积负反馈回路的影响，同时也受星球平均反射率负反馈回路的影响。星球平均反射率是由黑、白雏菊的反射率与覆盖面积决定的。

黑雏菊的4个反馈回路中，2个也是与分布面积有关的正、负反馈回路;另外2个是与增长率相关的负反馈回路。

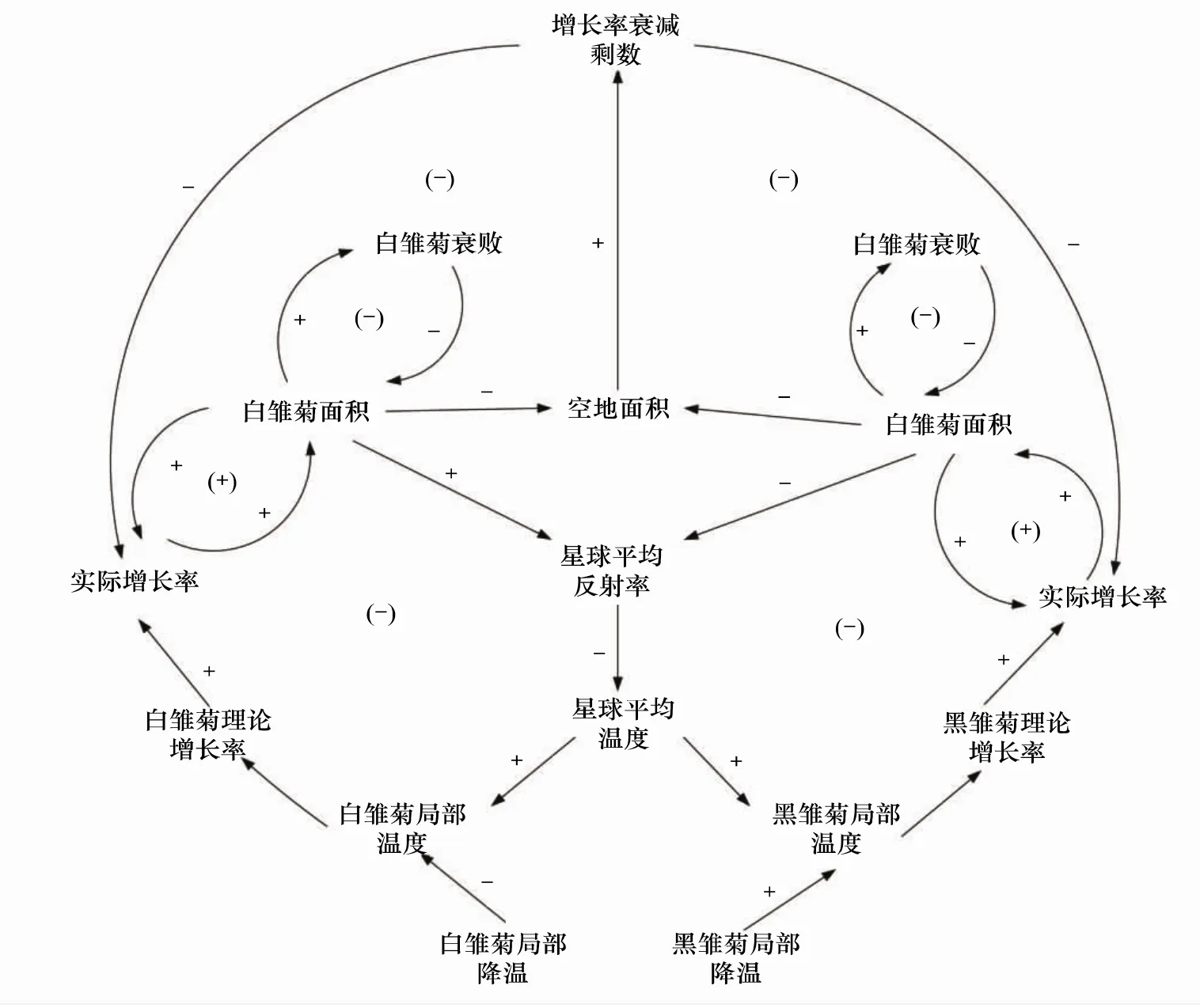
图3 雏菊世界因果反馈回路图(改自安德鲁·福特［26］)Fig.3 Casuality feedback loop diagram of Daisyworld(revised from Fort，2011［26］)

3 敏感性分析

3.1 初始面积的敏感性分析

假设不同的地面覆盖物的反射率分别为:白雏菊0.75;裸地0.5;黑雏菊0.25。

在Stella软件环境下，模拟不同初始面积分配条件下的雏菊世界温度变化情况，得到结果如图4所示。结果显示，在A、B、C三种初始面积组合条件下，虽然起始星球平均温度不同，但达到稳定状态后的星球平均温度均为21.55℃，表明雏菊世界稳定时的星球平均温度对于初始面积分配不敏感。

3.2 反射率的敏感性分析

图4 雏菊世界温度调节初始面积敏感性分析Fig.4 Initial area sensibility analysis of Daisyworld's temperature regulation

在Stella软件环境下，模拟3组不同地面覆盖物反射率条件下的雏菊世界温度变化情况，得到结果如图5:在A、B、C3种反射率组合条件下，虽然起始星球平均温度不同，但达到稳定状态后的星球平均温度均为21.55℃，表明雏菊世界稳定时的星球温度对于地面覆盖物反射率条件不敏感。

值得一提的是，在C反射率组合下，星球平均温度经过约500次模拟(即约500a)才达到稳定状态，而其他两种组合只需要几十次模拟就可以达到稳定状态。究其原因，是因为C组合中，黑、白雏菊的反射率与裸地差别不大，导致黑、白雏菊面积变化相对较慢。表明，虽然雏菊世界稳定状态时的星球温度对于地面覆盖物反射率条件不敏感，但是覆盖物反射率组合却影响雏菊世界达到稳定状态的时间。

4 讨论

本文基于雏菊世界模型，运用系统动力学的方法，通过stella软件求解不同初始面积分配与反射率组合条件下星球温度的稳定值，用简单且易于操作的方法论证了盖娅假说。结果证明，雏菊世界的星球温度对于初始面积分配、光照反射率条件均不敏感，在不同的初始面积分配以及不同的反射率条件下，雏菊世界稳定状态时最终都达到21.55℃。同时，通过模拟发现，星球覆盖物反射率组合影响星球达到稳定状态所需要的时间。

雏菊世界模型的优点在于通过简单的反馈关系揭示了在没有人为控制的情况下，地球系统水平的环境条件可以通过生物个体水平的自然选择与竞争实现自我调节，保持稳定，从而使环境条件有利于生物的群体生长。这对于那些没有受过系统分析训练，或不习惯系统思考的人，确实是个很好的启示，能够改变人们的思维习惯。因此，雏菊世界模型现在被广泛地用做教学案例。

然而，相比复杂的真实地球系统，雏菊世界模型还是过于简单。综合体现在以下5个方面:

(1)在雏菊世界原型中，太阳光照强度是不断增强的，但在本研究中，为了简化模拟，假定太阳辐射值为恒定。因此，本研究没有模拟太阳辐射强度变化对星球温度的长期(几十亿年)影响。

(2)只有温度一个环境变量。现实世界中，对生物有影响的环境变量还有水文、地形、地貌、养分、大气组成等，这些变量模型都没有包含进去。

(3)调节环境变量的生物只考虑非常简单的黑、白雏菊，不包含其他植物、动物、微生物。在现实世界中，黑雏菊很少见，而且单黑、白两种雏菊很难代表所有植物对光的反映，更不用说用雏菊来代表动物和微生物。而从调节大气温度的角度考虑，微生物所起的作用更关键。既使修正后的模型把兔子、狐狸等考虑进去，但比起真实地球系统的复杂性，显然远远不够。

图5 雏菊世界温度调节反射率敏感性分析Fig.5 Albedo sensibility analysis of Daisyworld's temperature regulation

(4)生物与环境反馈关系过于简单。雏菊模型只包含一个温度-生长的反馈关系，现实世界中则存在着多种环境变量与不同的生物之间的高度复杂的反馈关系。生物的某些行为，例如呼吸、新陈代谢、应激反应、生殖等，显然与环境变化也有重要关系。另外，生物多样性与环境调节功能的反馈关系也是未来需要进一步研究的焦点问题。

(5)雏菊模型只考虑生物-环境关系，没有考虑人为活动的影响。当前，人类活动显著改变着地球陆地、海洋、大气、岩石等圈层，并影响生物组成、结构与分布。在这样的背景下，盖娅假说如果不考虑人为因素的影响，其得出的结论往往与现实相悖。例如，盖娅假说预测大气组成将受生物过程的调节，并保持适合生物生存的水平。但自从工业革命以来，地球大气CO2浓度已经上升了35%，生物圈吸收CO2的速度却只提高了2%［27］。上述现象，Lovelock在《盖娅的复仇》和《盖娅消失的面孔:最后的警告》中也提到了，他认为“地球即将进入一个长达10万年的病态发热期”［18，28］。

因此，如前演示，这样一个极度简化的雏菊世界模型必然呈现简单的系统行为。由于盖娅假说主要考虑生物-环境的关系，没有将人类活动考虑进去，最近全球变化的许多事实都在盖娅假说的讨论范围之外。为了使模型与现实世界更相符，迫切需要设计更为精细的模型，包含更多的环境、生物变量以及反馈关系和人类活动因素，最终能够将盖娅系统融入到自然-人类耦合的大系统中。

［1］ Lovelock J E.Gaia，A New Look at Life on Earth.Oxford:Oxford University Press，1979.

［2］ Cannon W B.The Wisdom of the Body.New York:W.W.Norton＆ Company，Inc，1932.

［3］ Lovelock J E，Margulis L.Atmospheric homeostasis by and for the biosphere:the gaia hypothesis.Tellus，1973，26(1/2):2-10.

［4］ Dawkins R.The Extended Phenotype:The Long Reach of the Gene(Popular Science).Revised Edition.Oxford:Oxford University Press，1999:236-236.

［5］ Lovelock J E.Daisy World-a cybernetic proof of the Gaia hypothesis.The Co-evolution Quarterly Summer，1983:66-72.

［6］ Watson A J，Lovelock J E.Biological homeostasis of the global environment:the parable of Daisyworld.Tellus B，1983，35B(4):284-289.

［7］ Lenton T M，Wilkinson D M.Developing the Gaia Theory:a response to the criticisms of Kirchner and Volk.Climatic Change，2003，58(1/2):1-12.

［8］ Doolittle W F.Is Nature Really Motherly?Spring:The CoEvolution Quarterly，1981:58-63.

［9］ Lovelock J E.The Ages of Gaia:A Biography of Our Living Earth，2nded.Oxford:Oxford University Press，1995:213-216.

［10］ Kirchner J W.The Gaia Hypothesis:fact，theory，and wishful thinking.Climatic Change，2002，52(4):391-408.

［11］ Lawton J.Earth system science.Science，2001，292(5524):1965-1965.

［12］ Lenton T M.Gaia and natural selection.Nature，1998，394(6692):439-447.

［13］ Hamilton W D.Ecology in the large:Gaia and Genghis Khan.Journal of Applied Ecology，1995，32(3):451-453.

［14］ Wilkinson D M.Is Gaia really conventional ecology?Oikos，1999，84(3):533-536.

［15］ Cohen J E，Rich A D.Interspecific competition affects temperature stability in daisyworld.Tellus，2000，52(3):980-984.

［16］ Dagg J L.Unconventional bed mates:Gaia and the selfish gene.Oikos，2002，96(1):182-186.

［17］ Kirchner J W.The Gaia Hypothesis:conjectures and refutations.Climatic Change，2003，58(1/2):21-45.

［18］ Lovelock J E.The Revenge of Gaia.New York:Basic Books，2006.

［19］ Lovelock J E.A numerical model for biodiversity.Philosophical Transactions:Biological Sciences，1992，338(1286):383-391.

［20］ Lenton T M，Lovelock J E.Daisyworld revisited:quantifying biological effects on planetary self-regulation.Tellus b，2001，53(3):288-305.

［21］ World A J，Ackland G J，Dyke J G，Williams W T P，Lenton T M.Daisyworld:a review.Reviews of Geophysics，2008，46，RG1001，doi:10.1029/2006RG000217.

［22］ Forrester J W.Industrial dynamics:a major breakthrough for decision makers.Harvard Business Review，1958，36(4):37-66.

［23］ Forrester J W.Industrial Dynamics.Cambridge Mass:MIT Press，1961.

［24］ Wang Q F.System Dynamics，Revised Edition.Beijing:Tsinghua University Press，1994.

［25］ Richmond B.An Introduction to Systems Thinking.Isee Systems，ISBN 0-9704921-1-1.

［26］ Andrew F.Modeling the Environment:An Introduction To System Dynamics Modeling Of Environmental Systems，2nd edition.Translated by Tang H P，Shi P J.Beijing:Science Press，2011.

［27］ Schimel D S，House J I，Hibbard K A，Bousquet P，Ciais P，Peylin P，Braswell B H，Apps M J，Baker D，Bondeau A，Canadell J，Churkina G，Cramer W，Denning A S，Field C B，Friedlingstein P，Goodale C，Heimann M，Houghton R A，Melillo J M，Moore B III，Murdiyarso D，Noble I，Pacala S W，Prentice I C，Raupach M R，Rayner P J，Scholes R J，Steffen W L，Wirth C.Recent patterns and mechanisms of carbon exchange by terrestrial ecosystems.Nature，2001，414(6860):169-172.

［28］ Lovelock J E.The Vanishing Face of Gaia:A Final Warning.New York:Basic Books，2009.

参考文献:

［24］ 王其潘.系统动力学(修订版).北京:清华大学出版社，1994.

［26］ 安德鲁·福特著.环境模拟-环境系统的系统动力学模型导论(第二版).唐海萍，史培军译.北京:科学出版社，2011:265-277.