基于规划理论的机械铲工作面参数优化方法研究

汤万钧，才庆祥

(中国矿业大学矿业学院，江苏 徐州 221008)

露天采矿活动规模巨大，系统复杂，影响因素繁多，如何实现高产、高效、低成本的目标对露天矿的设计和管理人员提出了很高的要求。

目前，机械铲在露天矿很多种类的工艺系统中都扮演着剥离、挖掘的关键作用，是相关露天矿生产能力的基础。所以，提高机械铲的工作效率，充分发挥机械铲的生产能力对露天矿生产能力的提高有重要的影响；此外，采掘带宽度、台阶高度等工作面参数对露天矿生产剥采比有着重要的影响，这直接决定着露天矿的经济效益。

鉴于此项工作的重要性，长期以来，中外众多学者对参数优化问题提出了很多理论[1-4]，传统的单个参数分别计算优化的方法仍然占着主导地位。但是露天矿生产系统的复杂性决定了各个参数之间并不是独立的，而是互相影响，互相约束，任何一个参数的变动都可能影响其他参数的取值，这样传统的固定变量减少约束条件从而分别计算单个参数的方法就很难得到理想的结果，因为这样计算出的结果只是在给定的假设条件下的某参数的最佳值，但它很难(除了极小的概率碰巧)是系统的最优值。

而规划理论则是解决这类问题的恰当方法[5]。应用该理论，可以很好的解决在一定目标下，各个参数的优化问题。例如实现生产能力最大或经济效益最大的目标下，各个参数的取值。

1 规划算法原理

该算法解决的问题类型如式(1)所示。

式中，x、b、beq、lb和ub都是向量，A和Aeq是矩阵，c(x)和ceq(x)都是返回向量的函数，f(x)得到的结果是标量。另外，f(x)、c(x)和ceq(x)都可以是非线形函数。

每个变量都有其取值范围，不同的变量之间也有相应的约束关系，满足这些方程组或不等式组的点共同构成了变量的可行域，也就是说，变量只能在可行域中取值，可行域中的值是满足所有约束条件的值。

目标函数是约束问题的核心，可以设置一个或者多个目标函数，例如在矿山优化中可以设置利润最大或产量最高的单个目标，也可以同时设置两个目标，进行多目标优化。

本文以露天矿产量最大化为目标函数，通过分析工作面参数之间的相互约束关系，建立约束方程组，结合工程可行性给出各个参数的取值范围，以此为可行域建立数学模型进行优化计算。

2 建立计算模型

建立的任何模型都只是实际系统原型的简化，因为既不可能也没必要把实际系统的所有细节都列举出来。如果在简化模型中能保留系统原型的一些本质特征，那么就可认为模型与系统原型是相似的，是可以用来描述原系统的。因此，实际建模时，必须在模型的简化与分析结果的准确性之间作出适当的折衷，这常是建模遵循的一条原则。

本节将建立一个露天矿机械铲开采工作面的简化模型，借此介绍模型的建立思路和基本方法：

首先做如下等价：机械铲每次走行之间的剥离物料的形状应该是一个两端具有同样弧度曲面的不规则的块体，块体体积计算比较复杂；但是因为每次走行距离相同，剥离量也大体相同，因此认为机械铲每次走行之间的剥离量等于规则的长方体的体积，这样的等价处理不改变每次移步的剥离量，并且使得该量简单易算。

然后做如下假定：假定爆堆形状为梯形爆堆；假定切片轮廓为圆弧形；假定机械铲按匀速回转，暂时忽略回转循环中的加速和减速过程；假定机械铲挖掘和卸载时间为定值；假定卸载位置和机械铲中心线连线垂直于工作面走向。

这些假定使得研究的问题得到了极大的简化，有利于建立模型；但是也使得计算模型和工程实际出现一定偏差。出现的偏差在于：①梯形爆堆形状和实际的爆堆形状之间存在一定差异，但是经验表明梯形爆堆计算的结果是可以接受的；②挖掘机匀速回转运动和实际回转运动之间存在一定差异，不过可以通过选择合理的速度值减小误差；基于以上简化建立的模型与工作面工程实际情况之间存在一定差距，但是通过以上分析可以看出来误差在可以接受的范围内，那么就可认为模型与系统原型是相似的，是可以用来描述原系统的[6-9]。

工作面参数如图1所示。图1中各个参数的含义为：m为机械铲移设步距；A为采掘带宽度；H为爆堆高度；S为机械铲走行一次剥离量。

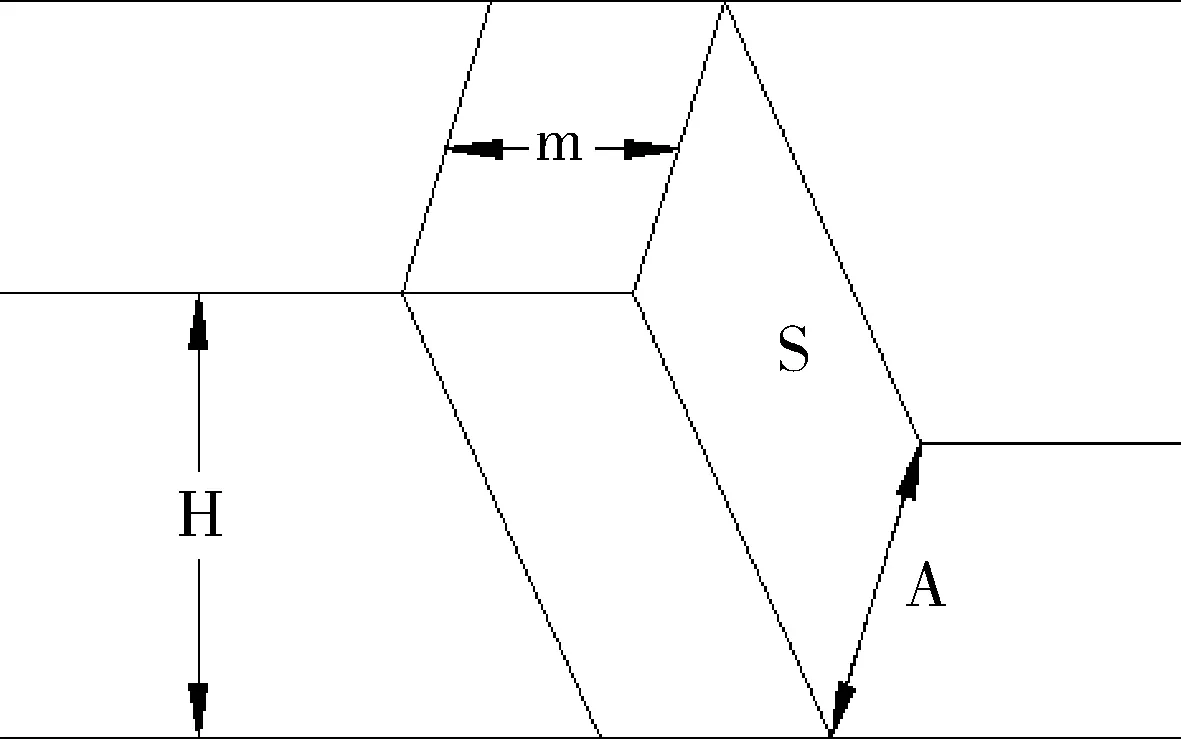
图1 工作面参数

设机械铲面对物料的摆动角度为α，机械铲剥离最外侧位置到卸载位置对中位置之间夹角为β且其不小于30°[10]，因为这是保证机械铲铲斗挖掘作业时和破碎机受料口不发生碰撞所要求的最小角度，事实上增加这个角度只会白白增加机械铲铲斗回转时间，因此β就取30°，假定机械铲与卸载位置的相对位置关系为连线与工作线延展方向成固定角γ，令挖掘机面对工作面的张角为α，电铲与收料装置之间保留安全距离，令其为β，位置关系如图2所示。

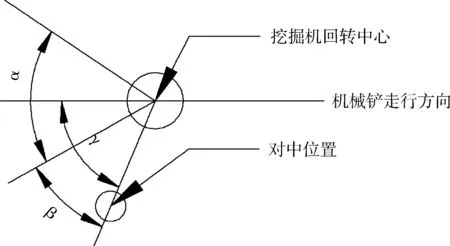
图2 机械铲与卸载位置关系

模型中变量之间的关系如式(2)～(14)所示。

机械铲走行一次剥离量

通过挖掘次数，机械铲走行一次剥离量又有

式中：n为剥离量S总共需要机械铲挖掘的斗数；V铲为机械铲斗容；A为满斗率。

机械铲一个挖掘循环用时

式中：tw为装载时间；ty为回转运输时间；tx为卸载时间；tq为其他时间。

其中，装载时间

式中Δtz为单次装载时间。

回转运输时间

式中：α为机械铲面对工作面的张角；β为机械铲最外工作位置与破碎机中心线连线的夹角；ω为机械铲铲斗回转角速度。

卸载时间

式中Δtx为单次卸载时间。

其他时间

式中Δtq为单次循环中的其他时间。

挖掘机挖完剥离量S所用时间

式中：tdz为机械铲走行时间；tpz为破碎机走行时间；tqf为清理平盘时间。

机械铲走行时间

式中vd为机械铲走行速度。

破碎机走行时间

式中vp为破碎机走行速度。

平盘宽度等于

式中rw为机械铲站立水平最大挖掘半径。

机械铲面对工作面挖掘角度满足

目标函数的选择可以从能力或经济不同的角度考虑，本次建模假设系统的首要任务是完成设计能力，即求系统单位时间的能力最大值，此时该模型的目标函数为

3 实例应用

给定平朔东露天矿的基本条件进行优化计算，上边模型的约束方程组中有一些式子并不是独立的，为减少未知数数量，减小优化工作量，我们将一些并不属于优化范畴的一些中间变量消去，并带入设备参数，例如我们指定rw=18m、Hwmax=16.8m、V铲=55m3等等，得到如下约束方程组。

考虑设备型号以及设计相关的制约，我们得到自变量的取值范围约束，如式(21)～(23)所示。

台阶高度需要大于2/3的推压轴高度，小于最大挖掘高度，计算得其取值范围如式(24)～(27)所示。

保证机械铲剥离最外侧位置与卸载位置的最小角度即为31°，故取值如式(28)～(29)所示。

通过计算，目标函数的最大值约为4620m3/h；而按照单因素分析优化的方法计算得到的参数，能力只有3500m3/h，增加了32%，优化效果十分明显。

系统的生产能力达到最大值时各项参数最终优化结果保留小数位后结果为：m≈3m，A≈31.8m，H≈16.8m，n≈30.68，α≈124°，β≈31°。

4 结论

通过这个简化模型的建立和求解过程可以看出规划理论在露天矿机械铲工作面参数优化方面可以发挥其快捷、系统、全面、准确的特点，能够得到目标

函数理论上的最优值，并给出对应的系统参数。

从模型的结构上看，模型具有开放性、易修改性和较强的适用性，只需要修正模型中的假设条件，即修正假设条件对应的约束方程，即可得到适用不同矿山条件下的精细模型，从而得到理想的优化结果。

[1] Caccetta L,Hill S P.An Application of Branch and Cut to Open Pit Mine Scheduling[J].journal of Global Optimization,2003,27(2):349-365.

[2] HOCHBAUM D S,CHEN A.PERFORMANCE ANALYSIS AND BEST IMPLEMENTATIONS OF OLD AND NEW ALGORITHMS FOR THE OPEN-PIT MINING PROBLEM[J].Operations Research,2000,48(6):894-914.

[3] 陈树召,才庆祥,尚涛,等.基于产量最大化目标的采掘带宽度优化模型[J].采矿与安全工程学报,2011,28(1):105-108.

[4] 尚涛，才庆祥，陈树召，等．带自移式破碎机半连续工艺系统工作面参数优化[J]．中国矿业大学学报，2010，39(6)：820-825．

[5] ERDE B,DURAN Z.model for extended bench casting in dipping coal seam[J].Journal of Scientific and Industrial Research,2007(6):435-438.

[6] 尚涛，顾正洪，才庆祥，等．东露天矿半连续工艺工作面布置方式优化研究[J]．露天采矿技术，2004(s1)：1-4．

[7] 姬长生．我国露天煤矿开采工艺发展状况综述[J]．采矿与安全工程学报，2008，25(3)：297-300.

[8] 于汝绶，张瑞新，王宝庭，等．露天采矿优化理论与实践[M]．北京：煤炭工业出版社，2005．

[9] 尚涛，才庆祥，张幼蒂，等．我国大型露天煤矿若干生产工艺问题分析[J]．中国矿业大学学报，2005，34(2)：138-142．

[10] 陈树召．大型露天煤矿他移式破碎站半连续工艺系统优化与应用研究[D]．徐州：中国矿业大学，2011．