滚压校直过程曲轴动态弹性形变分析
2013-12-14燕松山牛文强陈晓辉曾凡琮江连会
燕松山,牛文强,陈晓辉,曾凡琮,江连会
(武汉理工大学机电工程学院,湖北武汉430070)
传统的曲轴滚压校直方法需要在滚压完成后,对曲轴进行几次测量与校直,这样不仅降低了校直效率,且精度一般。在线测量与校直能够实现一次性准确校直,大大提高了校直的效率和精度。但在曲轴滚压校直加工过程中,曲轴受到滚压力、顶尖夹紧力及由滚压钳自身产生的惯性力对曲轴的作用,从而产生曲轴整体的弹性变形,造成在线测量结果的误差。而如果该弹性变形量过大,超出了曲轴滚压校直的范围,则在线校直失去意义,无法实现。如果该变形量处于允许的误差范围之内,则实现在线检测与校直便成为了可能,这样在滚压校直过程中就可以剔除弹性变形量,得出准确的待修正塑性变形量,这对提高滚压校直精度、改善曲轴滚压质量具有非常重要的工程意义。
曲轴滚压校直过程是一动态过程,在线检测中,往往关心的是测量机上的实时数据,即每个相位时刻的弹性变形情况,而不是某一时刻。通常的静态分析模型只能得出某几个时刻的变形情况,而很难准确地反映出整个过程中的变化,因此需要通过建立动力学模型来研究。通过借助ANSYS 有限元仿真软件,建立了曲轴滚压校直机构的动力学分析模型,对顶尖力及滚压钳惯性力对曲轴整体变形动态影响规律进行了分析。该研究对于曲轴滚压校直在线检测与校直系统的设计具有重要的指导意义。
1 滚压校直机构分析模型的建立与简化
针对该问题,需要对整个滚压模型加以研究。滚压过程是动态过程,滚压机构复杂,求解繁琐,因此需要在保证求解精度的前提下对模型进行简化。选取试验用四缸曲轴为研究对象,在滚压过程中,只有4个连杆颈上的滚压钳是随着曲轴的旋转而运动的,因此,只考虑作用于连杆颈上的4 个滚压钳所产生的惯性力。
对于单个的滚压钳,结构复杂,无法直接进行有限元网格划分,所以需要对钳体进行必要的简化。简化的目标:(1)考虑网格的划分;(2)要保证在整个简化过程前后滚压钳的质心与质量保持不变[6];(3)剔除不必要的零件(如油缸、支撑架等)。作者依据以上简化目标,将整个滚压模型简化为图1 所示的滚压机构[7],由于在测量中不存在滚压力,因此滚压钳与曲轴的接触可以看成joint 连接。

图1 滚压系统动力学仿真模型
2 数学模型的建立
分析可知,该模型可以简化为图2 所示的曲柄摇杆机构[8]。由此得出机构的运动方程:
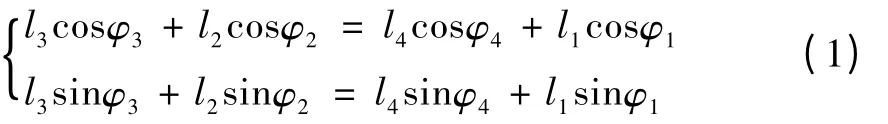
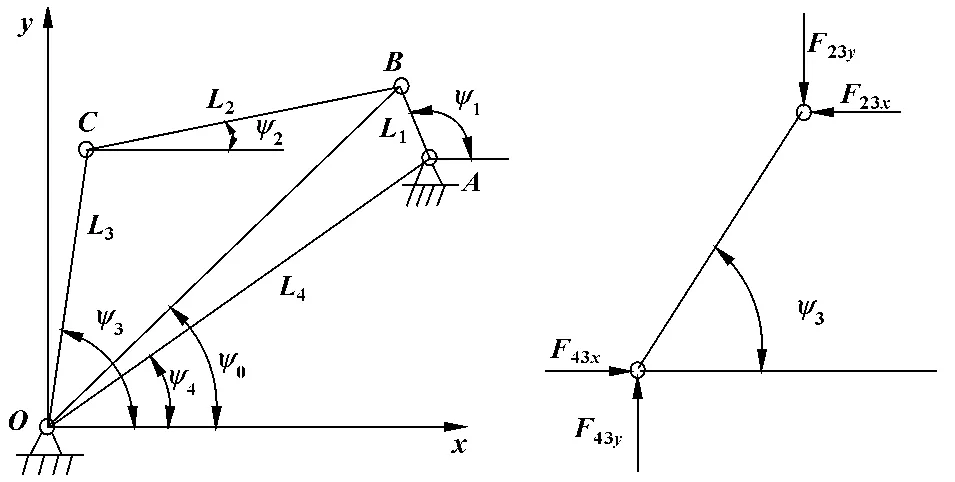
图2 曲柄摇杆机构运动模型
对方程求导可得出连杆的角速度ω2和角加速度ε2、摇杆的角速度ω3和角加速度ε3的方程为:
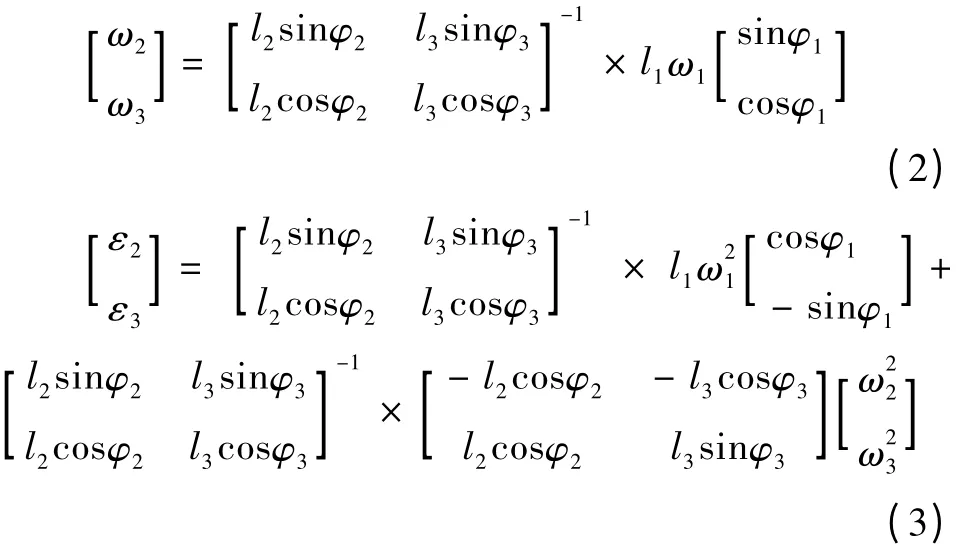
运用动力学方程C=inv(A)* B 及杆件受力分析可得下面的方程:
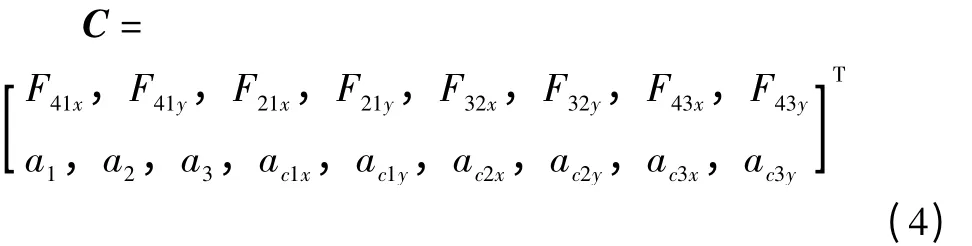
根据式(4)可得每个铰链的受力情况及受力大小。
通过建立曲柄摇杆机构的数学模型,并对机构进行运动分析和动力学分析,考虑铰链作用力的同时需要考虑杆件的自重及重心的偏移等因素,再结合材料参数进行力学分析,得出曲轴各个主轴颈的最大径向跳动量。
3 有限元分析结果
需要研究曲轴在旋转过程中每个相位角的曲轴弹性变形情况,如果使用经典ANSYS,由于模型复杂且计算量极大,很难实现。而基于ANSYS 的Workbench 中Transient Structure 模块提供了一种在惯性效应不可忽略的条件下,专门用来分析柔性体在任何随时间变化载荷作用下结构响应的方法。因此作者采用WB 来处理该问题。
由于曲轴型号众多(材料、轴颈等参数不尽相同),文中不可能一一讨论,因此,选用试验用四缸曲轴为研究对象[9],材料为QT700-2 球墨铸铁,详见表1。

表1 材料参数
理论假设: (1)材料是均匀的、连续的; (2)整个过程是在恒温下进行。自由网格划分对实体模型的几何形状无特殊要求,考虑到曲轴结构复杂且不规则,因此采用Workbench 的自由网格划分,生成的最终有限元模型如图1 所示,共包含单元数23 051 个,节点数43 108 个。
3.1 曲轴转速为30 r/min 的曲轴弹性变形规律分析
取曲轴转速为30 r/min (即约为3.14 rad/s),此处仅考虑连杆颈滚压钳惯性力对曲轴整体弹性变形的影响(顶尖力为2.5 MPa),6 s 内曲轴的应变结果最大为14.303 MPa,最小为1.1233 ×10-5MPa,如图3所示,节点求解结果显示最大应力发生在轴端连接处,紧接着是连杆颈连接处,然后是2、4 号主轴颈处,发生最小应力的地方为3 号主轴颈处。这说明曲轴在该时刻,大致呈向下凹的趋势,且靠近1 号主轴颈的轴端相对于5 号主轴颈曲率更大,这符合理论分析结果[10-11]。

图3 30 r/min 曲轴的等效应力云图
通过workbench 中的probe 后处理分别测得1、2、3、4、5 号主轴颈在不同相位中的变形量如图4 所示。不难看出:第一个周期由于速度从0 到3.14 rad/s 过渡,所以不稳定,之后的两个周期趋于稳定;3 轴的变形量最大,然后依次为2 轴、4 轴、1 轴、5轴,其中3 轴在t=4.067 1 s 时的跳动量6.01 ×10-2mm 为最大径向跳动。由于与顶尖相连的轴段较长(长于夹头夹紧的轴段几倍),因此2 轴径向跳动量略大于4 轴,1 轴略大于5 轴,故分析结果符合实际情况。
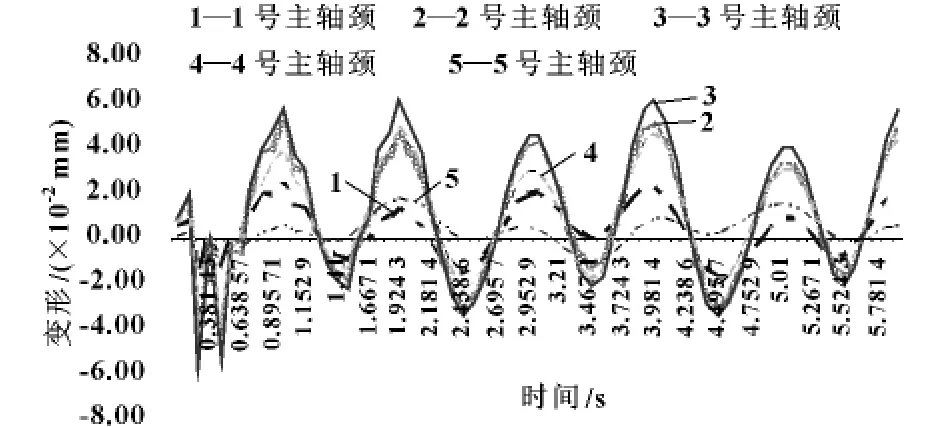
图4 3.14 rad/s 转速下曲轴各个主轴颈的径向跳动
选取3 轴作为研究对象,通过研究发现顶尖力的大小对曲轴的弹性变形也会有一定影响,如图5 所示。不难看出曲轴分别在顶尖力为0、2.5、3 MPa 时曲轴的弹性变形情况,最大变形都发生在t =4.067 1 s,大 小 分 别 为6.01 × 10-2、7.73 × 10-2、8.82 ×10-2mm。由数据可知,顶尖力的大小对曲轴变形的影响与滚压钳惯性力的影响为同一数量级,且变形量随顶尖力增大而逐渐增大,因此在讨论曲轴的整体变形时,顶尖力大小必须考虑在内。
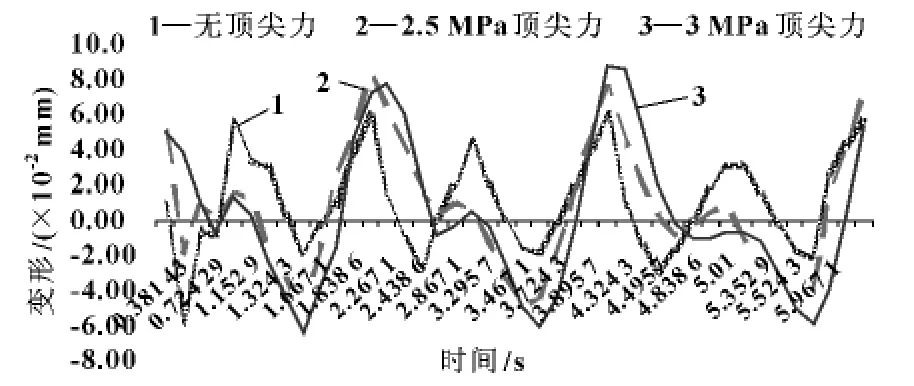
图5 顶尖力大小对曲轴弹性变形的影响
3.2 曲轴在不同转速下的弹性变形规律分析
为了讨论转速对曲轴变形的影响,此处将顶尖力设为固定值,仍然选择3 号主轴颈作为研究对象,分别讨论了曲轴转速分别为30、40、50 r/min 情况下曲轴3 号主轴颈每一个相位的弹性变形量。设初始相位为图1 所示位置,随着曲轴的转动,相位角依次增大,数值分析结果如图6 所示。由结果可知:在第二个周期的0.492 8 rad 相位角时3 号主轴颈的径向跳动量达到最大,3 轴最大的径向跳动分别为8.57 ×10-2、8.74 ×10-2、8.94 ×10-2mm,不难看出随着转速的增大,曲轴的变形量也随之增大,但该大小依然处于1 mm 以内,满足精度要求。因此,转速对于曲轴的影响可以忽略[12]。
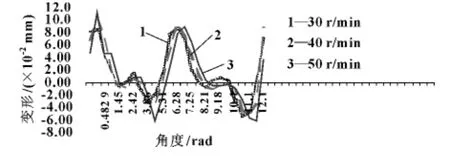
图6 曲轴不同转速大小对弹性变形的影响
3.3 数值分析与实验结果对比
为了验证数值分析的准确性,选取四缸曲轴作为研究对象,在042 滚压机床上进行实验测量,其中,在滚压校直测量中,撤消滚压钳口的滚压力,尾架顶尖力大小为2.5 MPa,主轴转速为30 r/min,分别测量了2 号、3 号主轴颈的径向跳动情况。测量结果如图6 所示,对于2 轴、3 轴,一个周期内,整体变形趋势与数值分析一致,最大变形量分别为104 和113 μm,与数值分析结果88.2 μm 相差2 ~3 mm 左右,满足精度要求,故数值分析结果处于可靠范围。
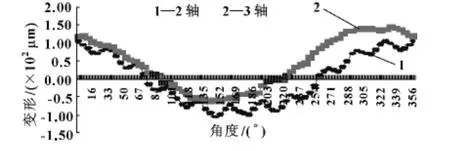
图7 主轴颈2 轴、3 轴实验结果
4 结论
通过对曲轴滚压测量与校直过程中滚压力、顶尖力及滚压钳惯性力对在线测量的影响规律分析,得出了以下结论:
(1)曲轴圆角滚压过程中,曲轴连杆颈上的滚压钳产生的惯性力引起的曲轴整体弹性变形规律;
(2)曲轴尾架顶尖力大小对曲轴整体弹性变形有相同数量级的影响,而滚压机转速为15 ~50 r/min时,对曲轴弹性变形的影响可以忽略不计;
(3)结合实验数据,验证了数值分析的准确性;
(4)在线校直工况中,曲轴弹性变形处于允许的误差范围内,在线校直方案可以实现。研究为圆角滚压机床在线测量与校直系统提供可靠的理论指导。
【1】李继凯.曲轴校直工艺探讨[J].汽车工艺与材料,2005(4):26 -30.
【2】戴海港.轴类零件弯曲变形在线检测研究[D].成都:西华大学,2011.
【3】张永军,韩红朝,李阳.基于弹性变形的齿轮测量精度有限元分析研究[J].哈尔滨理工大学学报,2011(2):66 -69.
【4】黄继雄,杨光,余先涛.曲轴圆角滚压变形分析与滚压校直专家系统的研究[J]. 组合机床与自动化加工技术,2005(11):66 -68.
【5】冯美斌,李满良,高凯.曲轴圆角滚压强化与滚压校直技术研究开发及应用[C]//12 届汽车材料年会,济南,2000:53 -60.
【6】HO Simon,LEE Yung-Li,KANG Hong-Tae,et al.Optimization of a Crankshaft Rolling Process for Durability[J]. International Journal of Fatigue,2009(5):799 -808.
【7】李建霞,王良才.基于Matlab 的四杆机构优化设计简介[J].机电设备开发与创新,2010,23(1):88 -89.
【8】孟维云. 曲柄摇杆机构综合优化设计及其软件开发[D].济南:山东建筑大学,2009.
【9】盛小兵. 曲轴圆角滚压强化工艺中曲轴变形的研究[D].武汉:武汉理工大学,2008.
【10】SPITERI Paul,HO Simon,LEE Yung-Li. Assessment of Bending Fatigue Limit for Crankshaft Sections with Inclusion of Residual Stresses[J].International Journal of Fatigue,2007(29):318 -329.
【11】成中清,蔡敢为,周晓蓉.6198 柴油机曲轴有限元分析[J].装备制造技术,2010(1):27 -32.
【12】朱正德.曲轴滚压校直——计算机辅助修正技术的典型应用[J].汽车技术,2000(8):15 -18.
