基于随机介质模型的GPR无单元法正演模拟
2013-12-14戴前伟王洪华
戴前伟,王洪华
(中南大学 地球科学与信息物理学院,长沙 410083)
探地雷达(Ground penetrating radar, GPR)具有高效、快速、无损、抗干扰能力强的优点,广泛应用于工程与环境地球物理探测的各个领域,成为浅部勘探的重要技术[1]。GPR正演模拟对数据解释具有重要的指导作用。通过对GPR模型的正演模拟,可以加深对GPR探测剖面的认识,提高解释精度[2]。目前,GPR正演模拟大都以传统的均匀介质为基础[3],而在实际的探地雷达检测中,地下介质中存在大量分布不规则的微小异常,将会造成大量小的不相干的扰动,其实质是源于介质在小尺度上的非均匀性,在实际高分辨GPR探测中常常作为“噪声”进行处理[4]。为了精细地研究地下介质的特征,必须对这种小尺度上的非均匀性产生的GPR波场有所了解[5]。显然,沿用传统的模型理论很难准确描述这些不可忽略的微小异常,而以统计学理论为基础的随机介质模型能较好地描述这种小尺度上的非均匀性特征[6]。
国内外很多学者对此进行了系统而深入的研究,IKELLE等[7]阐述了基于指数型椭圆自相关函数的二维随机介质模型的建立方法,并讨论了随机介质对弹性波场的影响特征。VARADAN等[8]研究了随机介质中弹性波的散射和衰减特征;KORN[9]采用时域有限差分法对二维随机介质模型进行了正演计算,并分析了随机介质对弹性波传播的影响特征;KNEIB和KERNER[10]进行了高精度、快速的随机介质模型的弹性波正演计算,并给出了随机介质模型的统计学描述方法;奚先和姚姚[11-13]系统研究了随机介质模型的建立方法及其特点,并对各种随机介质模型进行了正演计算;郭乃川等[14]提出了一种拓展了小尺度非均匀性择优取向的随机介质建模新方法,并利用三维锥形函数表达式压制计算误差,使得建立的随机介质模型更具有可信度。朱生旺等[15]采用随机介质模型方法构建了孔洞性油气储层模型;陈可洋[16]提出了三维随机介质建模方法,并对随机介质中的弹性波波场特征进行了分析;王金山等[17]提出了一种局部随机位置或固定位置任意形状截取法并结合多尺度建模技术来共同构造随机介质模型的新方法。目前,地球物理勘探中有关随机介质模型构建及其正演模拟的研究主要集中在地震勘探中。
无单元法(Element free method, EFM)是GPR正演模拟的有效手段。无单元法的基本思想[18]是将计算区域离散成若干个点,由滑动最小二乘法(Moving least squares,MLS)来拟合场函数,从而摆脱了单元的束缚,具有更大的灵活性。无单元法由于抛弃了单元的概念,只需节点信息,及采用滑动最小二乘法构造形函数,使得 EFM 具有前处理简单、精度高、独立变量解高次连续等优点。无单元法已应用于GPR正演模拟中,并取得了良好的效果。本文作者在上述理论的基础上,根据随机介质模型构建理论,构建多尺度的二维GPR随机介质模型,然后采用无单元法进行正演计算,研究了随机介质中GPR波场特征,并与均匀介质的计算结果进行了对比。
1 随机介质模型
随机介质模型主要由非均匀性大、小两种尺度组成。大尺度描述介质的背景特性,而小尺度则描述加在背景模型上的随机扰动。随机介质模型通常用一个均值为零的二阶平稳随机过程来描述[19]。在探地雷达(GPR)探测过程中,GPR波在地下介质中传播时主要受介电常数ε和介质的电阻率σ的影响。以二维随机介质为例,根据随机介质模型的构建理论,地下介质的参数可以表示为
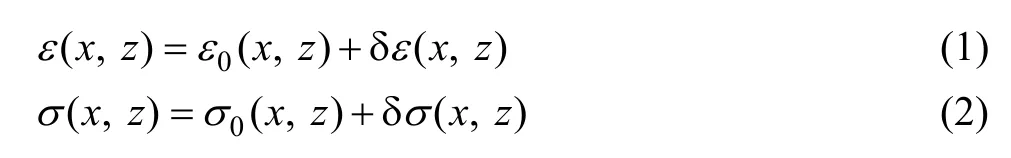
式中:ε0、σ0代表背景介质参数,δε、δσ代表上述背景介质上的非均匀扰动量,用来描述随机介质在小尺度上的非均匀性,
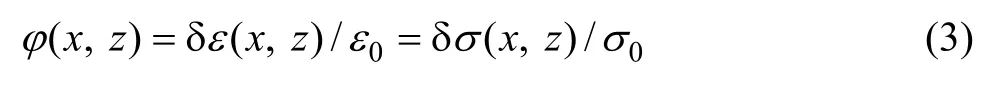
假设空间随机扰动φ具有零均值、一定方差及自相关函数的空间平稳随机过程,则

构造二阶平稳过程ε(x,z),σ(x,z)的步骤如下[19-20]:
1)选择自相关函数。目前,高斯型、指数型及Von KARMAN型自相关函数被广泛地应用于描述随机介质。高斯型相关函数能描述单尺度平滑的随机介质,指数型和Von KARMAN型相关函数能很好地描述具有多尺度平滑的随机介质。本文作者使用如下的混合型自相关函数:
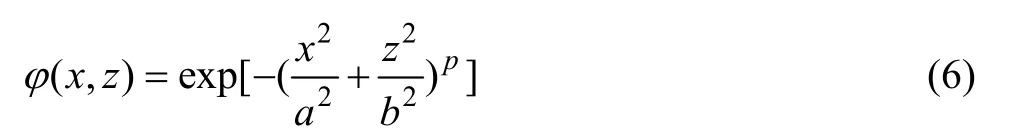
式中:a、b分别是介质在x、z方向上的自相关长度,p为粗糙度因子。当p=0, 1时,φ(x,z)分别对应高斯型自相关函数和指数型自相关函数。
3)用随机数发生器生成0, 2π[]φ上服从均匀分布的独立的二维随机场
4)应用下式计算随机功率谱:
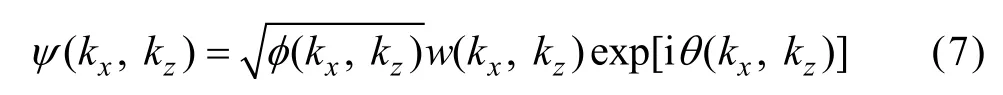

7)通过规范化产生均值为零、方差为2α,得到介电常数的小尺度相对扰动:

8)将式(10)代入式(1)中,即可得到随机介质模型的相对介电常数。随机介质模型的电导率也可按上述方法构建。
图1所示为按照上述方法,分别选择不同的相关长度a、b所产生的4个不同特征的随机介质(相对介电常数),其中背景相对介电常数为3,随机扰动量的标准差为 10%。从图1可以看到:自相关长度a、b可以描述随机介质扰动的平均尺度,随机介质模型能灵活、有效地描述地下实际介质分布。
2 GPR无单元法正演模拟
MAXWELL方程组描述了电磁场的运动学和动力学规律。由电磁波理论,高频电磁波(GPR)在介质中的传播规律也应服从MAXWELL方程组。以电场为例,根据文献[21]的推导,GPR波满足的波动方程为

式中:ε为介电常数(F/m),μ为磁导率(H/m),σ为电导率(S/m),E为电场强度(V/m),SE为电场源,t为时间。
首先定义如下形式的近似解函数:
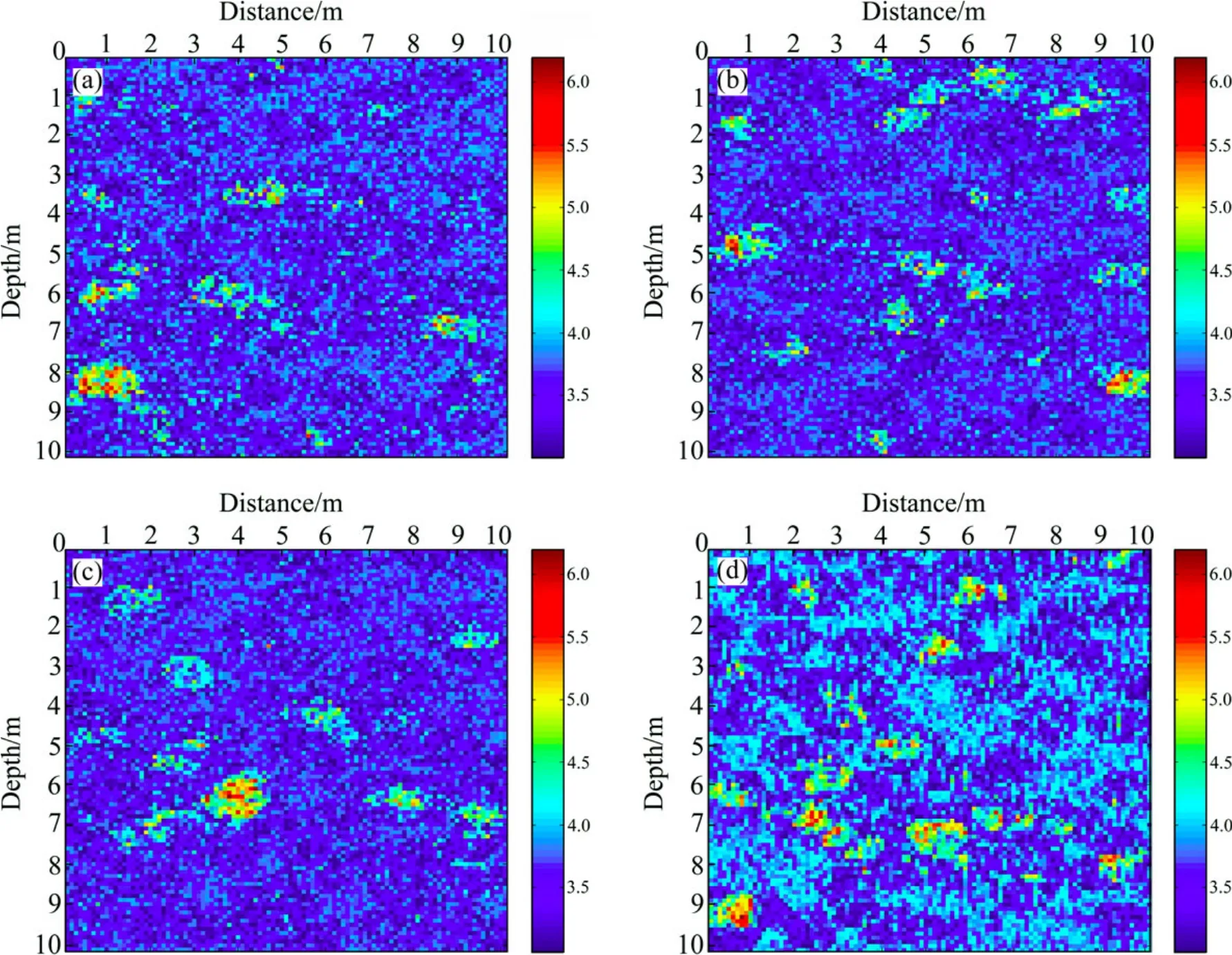
图1 采用混合型椭圆自相关函数产生的不同相关长度的随机介质相对介电常数模型Fig.1 Random medium models of relative dielectric permittivity in different auto correlation length media produced with intermixed ellipsoidal autocorrelation function: (a)a=1, b=1; (b)a=1, b=5; (c)a=5, b=5; (d)a=1, b=20
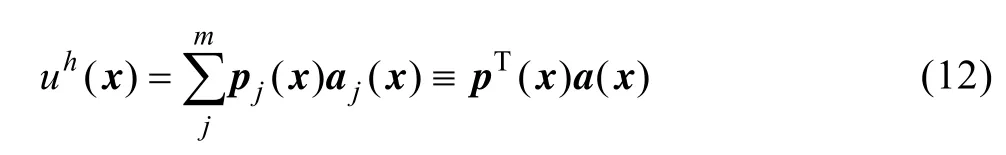
对式(12)加权求和得:
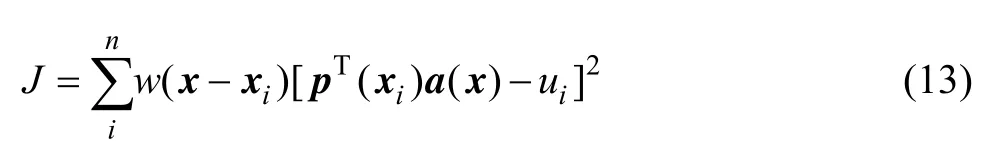
式中:n为权函数w(x-xi)非零域内的节点个数,在点x周围一个有限的邻域内,权函数w(x-xi)>0;在这个邻域之外的权函数定义为0,该邻域叫做点x的影响域[18],w(x-xi)的大小随着邻域点xi远离中心点x而逐渐减小。本文中采用指数权函数:
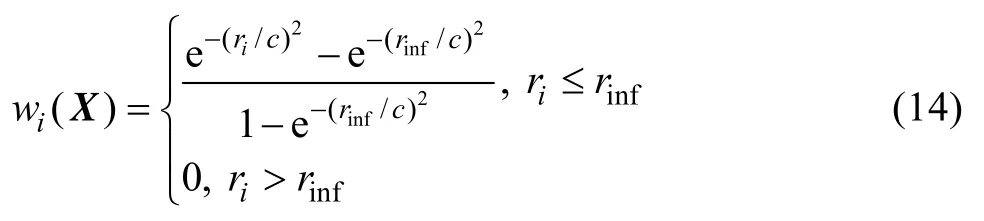
式中:rinf决定影响域的大小,在二维情况下,影响半径ri是点x与点xi之间的距离,c是一个控制相对权重的常数。
对式(13)求最小值可得:

式中:
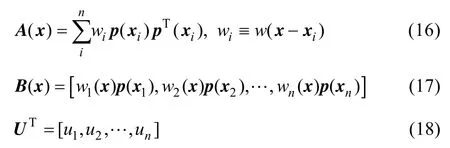
将式(15)代入式(12)中可得:
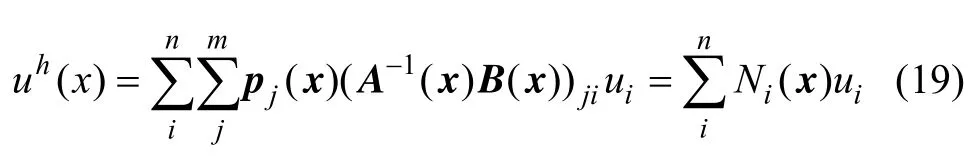
式中:Ni(x)为节点i的形函数,它是坐标的函数。
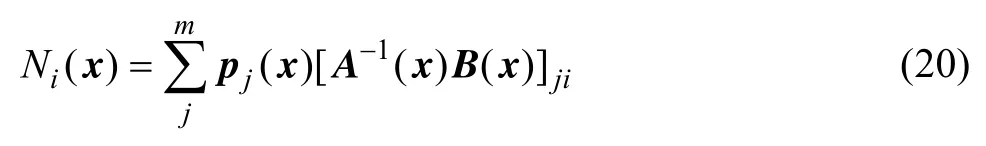
与有限元法类似,将式(19)通过变分原理用于式(11), 即得到空间上的离散方程。假设给定了基本边界条件, 使用带罚因子的 GALERKIN 方法[22]可得到如下离散方程:

式中:S为等效的电场源向量,为电场对时间的二次导数项,为电场对时间的一次导数项,M为质量矩阵,K’为阻尼矩阵,K为刚度矩阵。
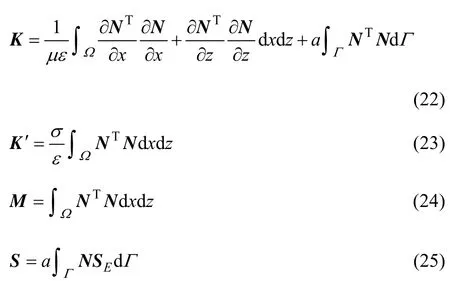
式中:Ω和Γ分别为所讨论电场的域及其边界,a为罚因子。以上各矩阵的求解都需要计算高斯数值积分。将式(22)在时间域中对加速度项E和速度项E采用中心差分法加以展开,

采用不完全LU分解预处理的BICGSTAB算法[23]进行迭代求解式(26)。为了提高计算效率,采用集中质量矩阵和集中阻尼矩阵使得方程组的求解无需对矩阵求逆。
3 数值模拟实例
设计了不含异常体的随机介质、包含矩形异常体随机介质2种GPR地电模型,应用基于随机介质模型的无单元算法对设定的模型进行了正演计算,分析了随机介质模型的GPR波散射特征,并与均匀介质模型的计算结果进行了对比分析。
3.1 模型1
图2所示为一个不含异常体的随机介质模型示意图,模型为一个10 m×10 m的矩形区域,其背景相对介电常数为ε为3.5,背景电导率σ为0.001 S/m,空间网格步长为0.1 m,网格总数为100×100。GPR波脉冲激励源的中心频率为100 MHz,时间步长为0.1 ns,时窗长度为50 ns。从图2中可以看出,在随机介质模型中含有几个小尺度的异常。应用无单元法对该模型进行正演计算,其模拟所得的GPR正演模拟剖面如图3所示。由图3可见,随机介质中的GPR波由于受到随机介质的影响散射现象非常强烈。
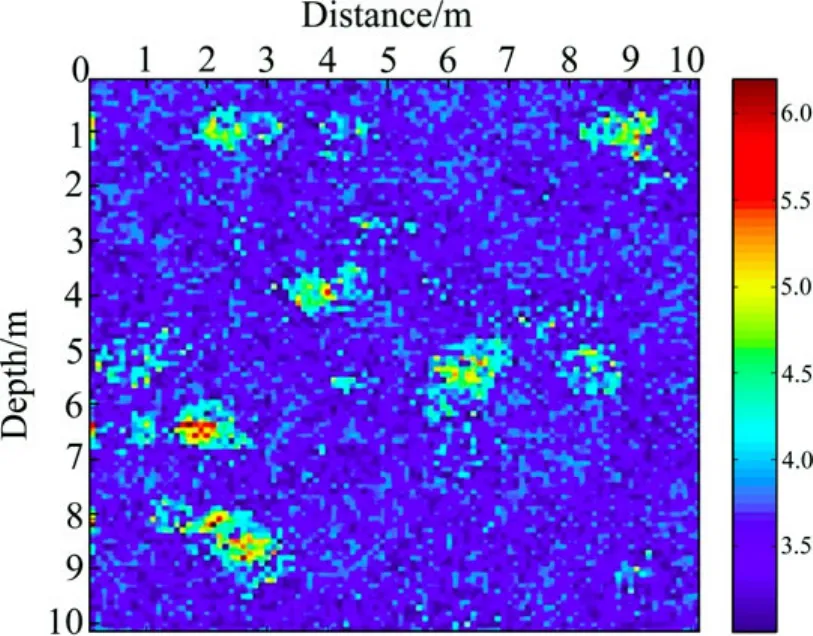
图2 随机介质模型示意图Fig.2 Sketch map of random medium model
为了更详细地说明GPR波在随机介质中的传播特征,将GPR波脉冲激励源放置在模型的中间位置(5.0,5.0),通过截取不同时刻GPR波场快照图,观测随机介质对GPR波传播的影响。应用无单元法对该随机介质模型进行正演模拟,得到如图4所示的波场快照,图4(a)、(b)、(c)所示分别为随机介质模型中 GPR波10、20、30 ns时刻的波场快照,图4(d)、(e)、(f)所示为相应时刻均匀介质(相对介电常数为 3.5)的波场快照。图4(a)、(b)、(c)与(d)、(e)、(f)相比,GPR 波波前由于受到小尺度异常散射的影响,波形发生扭曲。此外,随机介质中 GPR波在传播过程中由于受到小尺度异常的影响散射现象非常强烈,并呈无序状。而均匀介质中GPR波波前都是标准的圆形,并且GPR波传播无散射现象出现。因此,在GPR数据处理过程中,准确认识地下介质的小尺度异常产生的GPR波散射特征是非常有必要的。
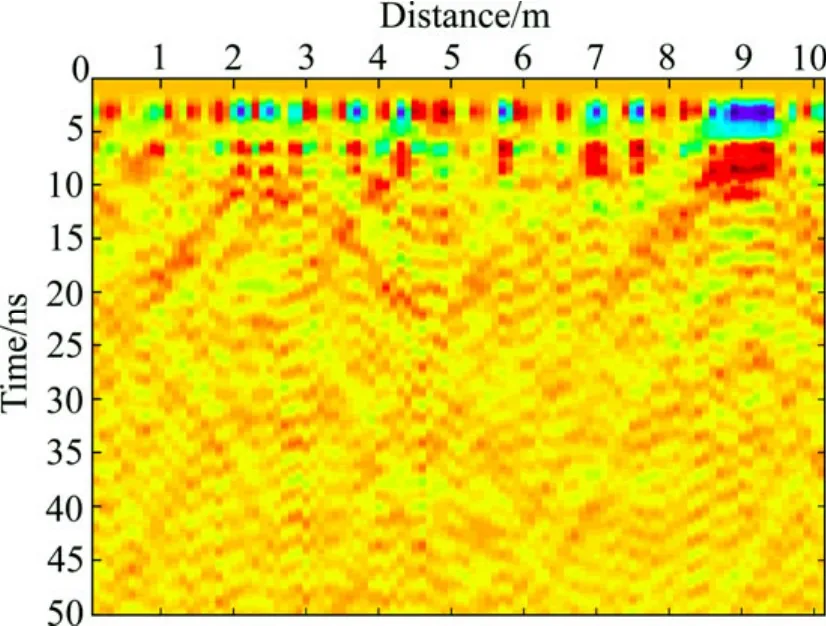
图3 模型1 GPR正演剖面图Fig.3 GPR forward compose section of Model 1
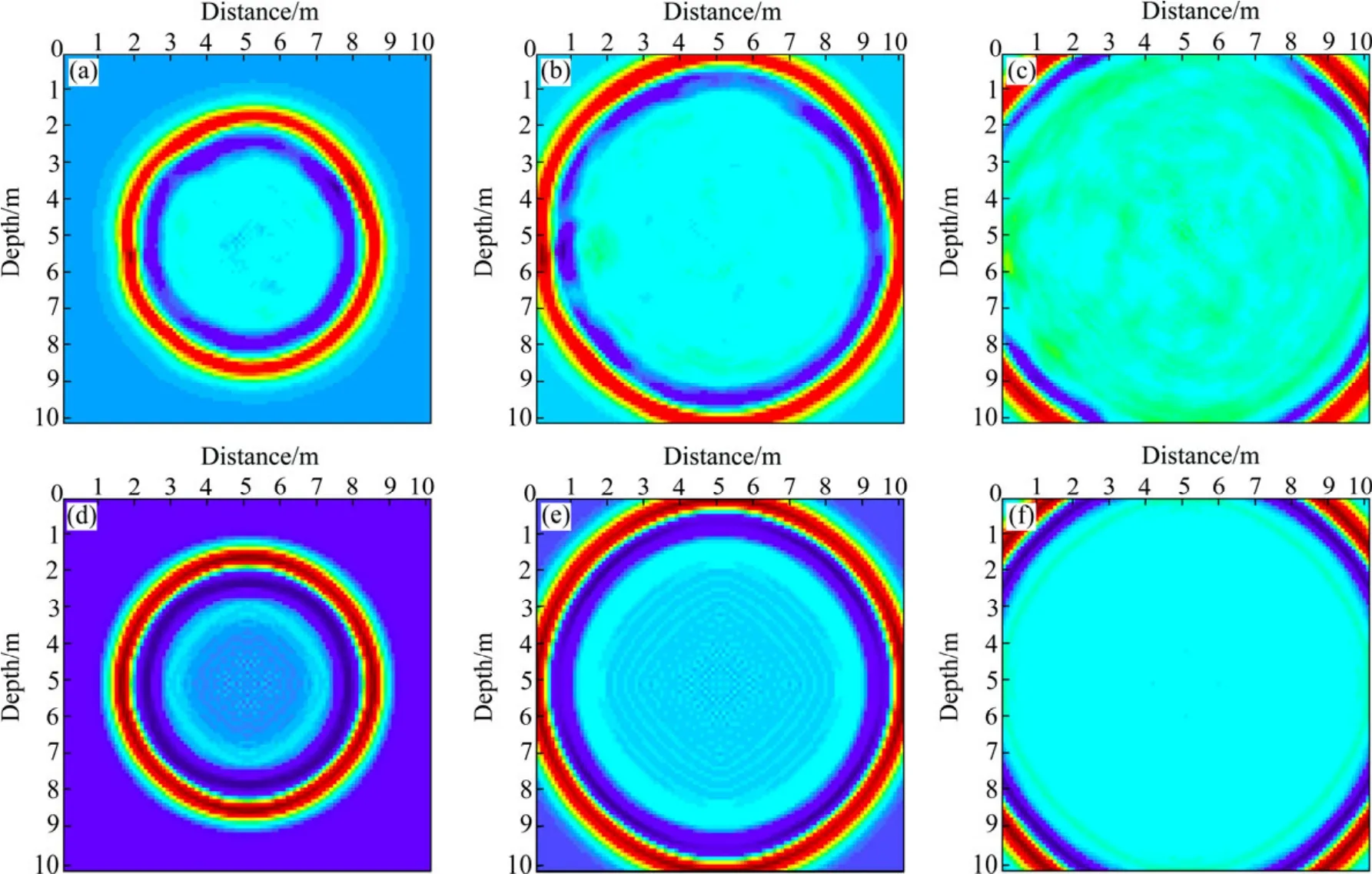
图4 随机介质模型与均匀介质模型的波场快照图Fig.4 Wave field snapshots of random medium model ((a), (b), (c))and homogeneous medium model ((d), (e), (f)): (a), (d)10 ns;(b), (e)20 ns; (c), (f)30 ns
3.2 模型 2

图5 模型2示意图Fig.5 Sketch map of random medium Model 2
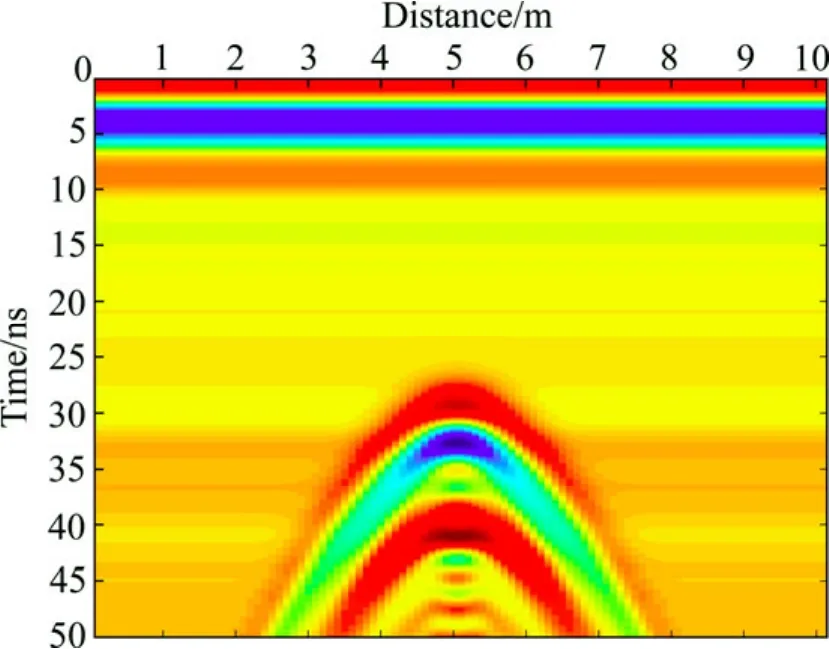
图6 均匀模型2 GPR正演剖面图Fig.6 GPR forward compose section of Model 2
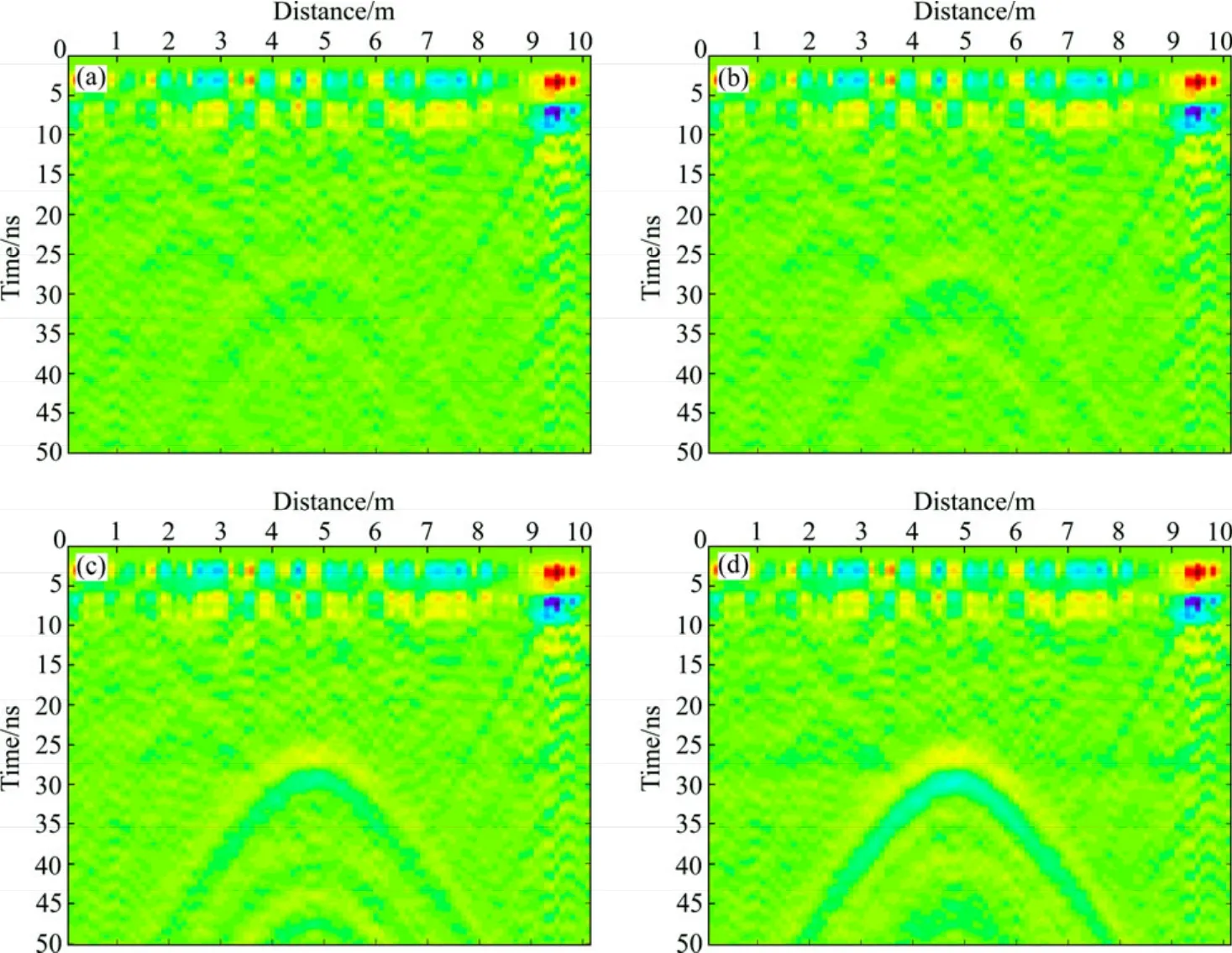
图7 矩形异常体中相对介电常数不同时的GPR正演模拟剖面图Fig.7 GPR forward compose section of rectangular anomalies with different relative dielectric permittivities: (a)6.0; (b)8.0;(c)10.0; (d)15.0
图5所示为含有矩形异常体的随机介质模型示意图,模型为一个10 m×6 m的矩形区域,其背景相对介电常数ε为3.5,背景电导率σ为0.001 S/m,随机介质模型在背景相对介电常数和背景电导率上进行扰动。坐标(5.0, 2.0)的位置有一个大小为0.6 m×0.4 m的矩形异常体,其相对介电常数ε1分别为6.0、8.0、10.0和15.0;电导率σ1为0.01 S/m。空间网格步长为0.1 m,网格总数为100×60。GPR波脉冲激励源的中心频率为100 MHz,时间步长为0.01 ns,时窗长度为50 ns, 具体参数如图5所示。应用无单元法分别对均匀介质模型(ε1为 8.0)和随机介质模型(ε1为 6.0、8.0、10.0和15.0)进行正演模拟,其模拟所得的GPR正演模拟剖面如图6和图7所示。由图6可见:矩形异常体的上界面为一水平反射界面,矩状异常体的两个棱角位置出现绕射波,由于矩形的顶边很短,导致矩形异常体的上边在雷达剖面图中近似为双曲线形弧形,非常清晰,矩形异常体的下界面与上界面类似。图7(a)、(b)、(c)和(d)所示分别为随机介质模型中矩形异常体的相对介电常数为6.0、8.0、10.0和15.0时得到的剖面图。由图7可知:雷达剖面图GPR波散射非常严重,但是,矩形异常体产生的双曲线反射弧形还是可见;由于GPR波散射现象的出现,使得双曲线弧形非常不光滑,甚至发生同相轴不连续的现象。对比图7(a)、(b)、(c)和(d)可知,随着矩形异常体与背景介电常数差异的增大,双曲线波形也越来越明显。但是,对比图6与图7(b)可以看到,当矩形异常体的相对介电常数保持不变时,矩形异常体在随机介质中产生的双曲线波形比在均匀介质中产生的双曲线波形更微弱。随机介质模型模拟所得的正演剖面与实测剖面更相符,具有更高的模拟精度,更有利于指导雷达剖面的数据解译。
4 结论
1)介绍了基于随机过程的谱分解理论和混合型自相关函数的随机介质模型构建方法,并详细阐述了随机介质模型的构造步骤,详细推导了无单元法求解GPR波动方程的具体解法。
2)两个随机介质的GPR模型算例结果表明:与均匀介质中GPR波的传播相比,随机介质中GPR波的传播由于受到小尺度异常的影响散射现象非常强烈,并且波形发生扭曲,随机介质中异常体产生的反射波形非常不光滑,甚至发生同相轴不连续的现象,并且反射波能量较弱。认识GPR波在随机介质中的传播规律,更有利于指导雷达实测剖面的数据解译。
[1]曾昭发, 刘四新.探地雷达原理与应用[M].北京: 电子工业出版社, 2010: 168-169.ZHENG Zhao-fa, LIU Si-xin.Ground penetrating radar theory and applications [M].Beijing: Electronic Industry Press, 2010:168-169.
[2]戴前伟, 王洪华, 冯德山, 陈德鹏.基于三角形剖分的复杂GPR模型有限元法正演模拟[J].中南大学学报: 自然科学版,2012, 43(7): 2668-2673.DAI Qian-wei, WANG Hong-hua, FENG De-shan, CHEN De-peng.Finite element method forward simulation for complex geoelectricity GPR model based on triangle mesh dissection [J].Journal of Central South University: Science and Technology,2012, 43(7): 2668-2673.
[3]JAMES I, ROSEMARY K.Numerical modeling of groundpenetrating radar in 2-D using MATLAB [J].Computers &Geosciences, 2006, 32(9): 1247-1258.
[4]黄真萍, 曹杰梅, 周成峰, 冯丽珍.探地雷达资料的高分辨去噪处理及应用[J].福州大学学报: 自然科学版, 2012, 40(4):521-526.HUANG Zhen-ping, CAO Jie-mei, ZHOU Cheng-feng, FENG Li-zhen.The high resolution de-noise processing of groundpenetrating radar data and its engineering application [J].Journal of Fuzhou University: Natural Science Edition, 2012, 40(4):521-526.
[5]奚 先, 姚 姚.二维随机介质及波动方程正演模拟[J].石油地球物理勘探, 2001, 36(5): 546-552.XI Xian, YAO Yao.2-D random media and wave equation forward modeling [J].Oil Geophysical Prospecting, 2001, 36(5):546-552.
[6]MICHAEL K, HARUO S.Synthesis of plane vector wave envelopes in two dimensional random elastic media based on the Markov approximation and comparison with finite-difference simulations [J].Geophysical Journal International, 2005, 161(3):839-848.
[7]IKELLE L, YUNG S, DAUBE F.2-D random media with ellipsoidal autocorrelation function [J].Geophysics, 1993, 58(4):576-588.
[8]VARADAN V K, MA Y, VARADAN V V.Scattering and attenuation of elastic waves in random media [J].Pageoph,131(4): 577-603.
[9]KORN M.Seismic wave in random media [J].Journal of Applied Geophysics, 1993, 29(3, 4): 247-269.
[10]KNEIB G, KERNER C.Accurate and efficient seismic modeling in random media [J].Geophysics, 1993, 58(4): 576-588.
[11]奚 先, 姚 姚.二维弹性随机介质中的波场特征[J].地球物理学进展, 2005, 20(1): 147-154.XI Xian, YAO Yao.The wave field characteristics in 2-D elastic random media [J].Progress in Geophysics, 2005, 20(1):147-154.
[12]奚 先, 姚 姚.随机介质模型的模拟与混合型随机介质[J].中国地质大学学报: 地球科学, 2002, 27(1): 67-71.XI Xian, YAO Yao.Simulations of random medium model and intermixed random medium [J].Journal of China University of Geosciences: Earth Science, 2002, 27(1): 67-71.
[13]奚 先, 姚 姚.随机介质模型正演模拟及其地震波场分析[J].石油物探, 2002, 41(1): 31-36.XI Xian, YAO Yao.Modeling in random medium and its seismic wave field analysis [J].Geophysical Prospecting for Petroleum, 2002, 41(1): 31-36.
[14]郭乃川, 王尚旭, 郭 锐, 啜晓宇.地震勘探中三维小尺度非均匀性随机介质模型的建立及其特点分析[J].石油天然气学报, 2012 34(7): 62-67.GUO Nai-chuan, WANG Shang-xu, GUO Rui, CHUAI Xiao-yu.Construction and feature analysis of three dimensional small scale inhomogeneities in seismic prospecting [J].Journal of Oil and Gas Technology, 2012, 34(7): 62-67.
[15]朱生旺, 魏修成, 曲寿利, 刘春园, 吴开龙.用随机介质模型方法描述孔洞型油气储层[J].地质学报, 2008, 82(3): 420-427.ZHU Sheng-wang, WEI Xiu-cheng, QU Shou-li, LIU Chun-yuan,WU Kai-long.Description of the carbonate karst reservoir with random media model [J].Acta Geologica Sinica, 2008, 82(3):420-427.
[16]陈可洋.三维随机建模方法及其波场分析[J].勘探地球物理进展, 2009, 32(5): 315-320.CHEN Ke-yang.3-D random modeling scheme and wave field simulation analysis [J].Progress in Exploration Geophysics,2009, 32(5): 315-320.
[17]王金山, 陈可洋, 吴清岭, 杨 微.随机介质模型的一种构造方法[J].物探与化探, 2010, 34(2): 191-194.WANG Jin-shan, CHEN Ke-yang, WU Qing-ling, YANG Wei.A construction method for random medium model [J].Geophysical & Geochemical Exploration, 2010, 34(2): 191-194.
[18]冯德山, 王洪华, 戴前伟.基于无单元法Galerkin法探地雷达正演模拟[J].地球物理学报, 2013, 56(1): 298-308.FENG De-shan, WANG Hong-hua, DAI Qian-wei.Forward simulation of ground penetrating radar based on the element free Galerkin method [J].Chinese Journal of Geophysics, 2013, 56(1):298-308.
[19]殷学鑫, 刘 洋.二维随机介质模型正演模拟及其波场分析[J].石油地球物理勘探, 2011, 46(6): 862-872.YIN Xue-xin, LIU Yang.Modeling in 2-D random medium and its wave field analysis [J].Oil Geophysical Prospecting, 2011,46(6): 862-872.
[20]JIANG Zi-meng, ZENG Zhao-fa, LI Jing, LIU Feng-shan, WU Feng-shou.Simulation and analysis of GPR signal based on stochastic media model [C]// Proceedings of the 14th International Conference on Ground Penetrating Radar.Shanghai: IEEE, 2012: 214-219.
[21]底青云, 王妙月.雷达波有限元仿真模拟[J].地球物理学报,1999, 42(6): 818-825.DI Qing-yun, WANG Miao-yue.2D finite element modeling for radar wave [J].Chinese Journal of Geophysics, 1999, 42(6):818-825.
[22]贾晓峰, 胡天跃, 王润秋.无单元法用于地震波波动方程模拟与成像[J].地球物理学进展, 2006, 21(1): 11-17.JIA Xiao-feng, HU Tian-yue, WANG Run-qiu.Wave equation modeling and imaging by using element free method [J].Progress in Geophysics, 2006, 21(1): 11-17.
[23]柳建新, 蒋鹏飞, 童晓忠, 徐凌华, 谢 维, 王 浩.不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J].中南大学学报: 自然科学版, 2009, 40(2):484-491.LIU Jian-xin, JIANG Peng-fei, TONG Xiao-zhong, XU Liang-hua, XIE Wei, WANG Hao.Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling [J].Journal of Central South University: Science and Technology, 2009,40(2): 484-491.
