木堆积结构光子晶体中辐射子簇的非指数衰减动力学研究

刘景锋 ，李凌燕

(华南农业大学理学院应用物理系，广东广州510642)

操控自发辐射是量子光学领域非常重要的研究课题，它决定了一系列光子电子器件的性能，例如，太阳能电池的转换效率、用于光通信和量子密钥分发的单光子源的量子效率、LED 的性能取决于自发辐射到衬底中的光子能否被有效萃取、激光器的阈值大小和模式调制的速度，等.

1946年，PURCELL 发现位于微腔中的辐射子自发辐射会增强(Purcell-效应). 此后，人们发现自发辐射有很强的环境依赖性. 因而，控制自发辐射，需要调控辐射子所在位置电磁模式的局域态密度.YABLONOVICH［1］和JOHN［2］研究发现，光子晶体可以有效地调制光子模式分布.此后，利用三维光子晶体控制自发辐射问题被广泛研究.

在实验方面实现大块完整的面心立方结构困难，而木堆积结构容易制备［3-10］. ISHIZAKI 等［10］在实验上实现并提出了木堆积结构三维光子晶体对光子的操纵的新方法，并且开创了光子晶体表面科学研究的新方向. 基于有机三维光子晶体中量子点的渗透［7，11］，GU 等［8］首次从实验上在近红外区观测到量子点自发辐射寿命和自发辐射光谱的巨大改变. 最近，ARAKAWA［12］首次从实验观察到木堆积光子晶体纳米微腔中的激光振荡. 然而很少利用全矢量的方法来研究木堆积结构中辐射子簇的非指数时间分辨衰减问题.

本文讨论木堆积结构中一簇辐射子的自发辐射衰减动力学. 利用自发辐射速率分布函数［13-14］研究辐射子簇的时间分辨荧光衰减，其结果可为实验上利用时间分辨荧光探测局域态密度［15-16］提供参考.

1 木堆积结构光子晶体对称性分析及带结构计算

木堆积结构属于金刚石晶格. 根据固体物理学知识，由球形基元构成的面心立方和金刚石结构，分别对应O5h和O7h群.但是，对于木堆积结构，其基元为3 根小柱子，其对称性比球的对称性低. 因而，木堆积不再像面心立方和金刚石结构一样具有48 重对称性，而是仅有16 重对称性. 木堆积结构满足的对称操作如下:{E|0}，{c2z|0}，{c2x|0}，{c2y|0}，{Ⅰc4z|0}，{|0}，{Ⅰc2xy|0}，{Ⅰc2xˉy|0}，{Ⅰ|τ}，{c4z|τ}，{|τ}，{c2xy|τ}，{c2xˉy|τ}，{Ⅰc2z|τ}，{Ⅰc2x|τ}，{Ⅰc2y|τ}.

木堆积结构光子晶体的示意图、布里渊区图及其能带结构如图1～图3 所示. 该结构由低折射率(1.552)的椭圆柱子堆积而成，相邻4 层柱子间的距离为c，每层内相邻2个柱子间距为d=1 000 nm，并且c/d =椭柱子横截面椭圆的长轴h 和短轴w的长度分别为375 nm 和150 nm，参数取自文献［7］的实验结果.图3 中，沿Γ-X 方向存在一个频率从0.912(2πc/a)到0.950(2πc/a)的赝带隙(如图3中灰色区域)，赝带隙的中心频率为0.931(2πc/a)(a 为光子晶体的晶格常数，c 为真空中的光速).

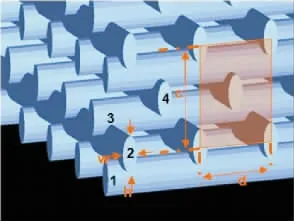
图1 木堆积结构示意图Figure 1 Schematic diagram of woodpile structure

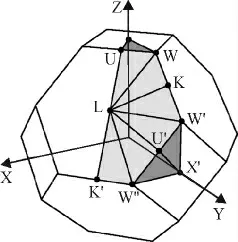
图2 木堆积结构的布里渊区图Figure 2 Brillouin zone diagram of woodpile structure

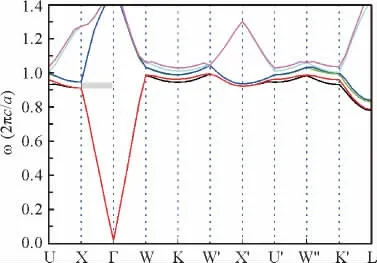
图3 木堆积光子晶体能带结构计算值Figure 3 Calculated band diagram of woodpile photonic crystals

2 自发辐射速率分布及衰减动力学函数的定义

为了解释时间分辨荧光的非单指数衰减动力学，首先定义自发辐射速率分布函数［17］为:

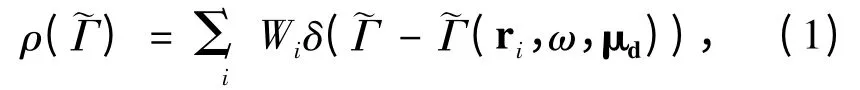
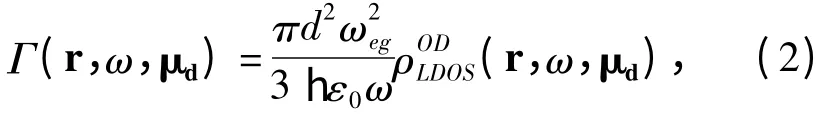
式中ωeg为辐射子的跃迁频率(r，ω，μd)为方向性局域态密度

式中对倒格矢k 的积分需在第一布里渊区内完成，ωnk和En(k，r)分别为对应带指标n 的本征频率和本征矢量.

如果大量辐射子分布在光子晶体的原胞内，并且偶极矩随机分布，相应的局域态密度［18-20］为

因而对应的方向平均速率分布函数［13，21］为

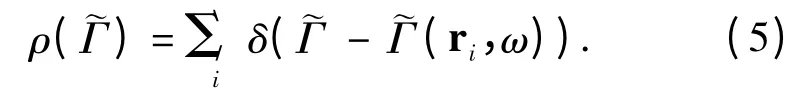
根据速率分布函数(5)，定义辐射子簇的时间分辨衰减函数为

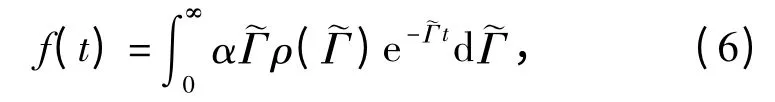
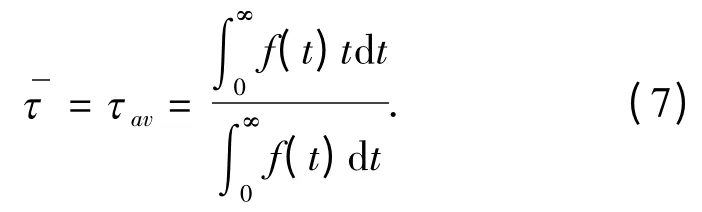
式(2)表明辐射子的自发辐射速率依赖局域态密度. 如果已知局域态密度，则可以解决微纳结构环境中的光与物质相互作用问题，从而分析辐射子的自发辐射特性. 但在实验上无法直接探测局域态密度，然而，可以探测处于激发态的辐射子自发辐射寿命，通过自发辐射寿命和自发辐射速率的关系，求得自发辐射速率，进而得到方向性局域态密度. 在理论上，如果讨论自发辐射问题，则必须讨论方向性态密度或局域态密度. 通过解电磁场的本征值方程，可得到本征值和本征矢量，从而得到方向性局域态密度和自发辐射速率分布.

3 结果与分析

木堆积结构中辐射子簇的自发辐射速率分布和时间分辨自发衰减动力学函数的计算过程及参数如下:采用MONKHORST 和PACK 的方法［23］把第一布里渊区分成16 384个粗格点和1 048 576个精细格点. 然后选择965个平面波解出磁场的本征方程［20］，求得粗格点上的本征矢量Hn(k，r)和本征值ωnk，然后根据本征电场和本征磁场的关系，得到本征电场En(k，r)［24］，最后利用插值法［23］来获得精细格点上的本征矢量En(k，r)和本征值ωnk.

计算的激发态辐射子簇的自发辐射速率分布及时间衰减动力学曲线如图4、图5 所示. 利用式(1)分别研究了赝带隙的下带边、中心和上带边3个不同跃迁频率的自发辐射速率分布，以真空中的自发辐射速率为参考速率(图4). 选择位于原胞内距离椭圆柱表面为3 nm、6 nm 这2 层上39 668个辐射子为研究对象. 结果表明，当辐射子位于空气中，且跃迁频率位于下带边或者赝带隙中心时，几乎所有辐射子的自发辐射过程都加速.然而，跃迁频率位于上带边时，几乎所有辐射子的自发辐射都减速，但总体上，上带边的辐射子自发辐射比赝带隙中心的更慢. 因此，在这种低折射率的木堆积结构光子晶体中，赝带隙效应不太明显. 在图5 中，黑实线对应于真空时辐射子的自发衰减动力学曲线，衰减曲线呈单指数下降. 跃迁频率位于赝带隙的下带边或者中心时，其衰减速率比真空中的衰减快，而位于赝带隙上带边时，其衰减速率比真空中的衰减慢.

图4 辐射子簇自发辐射速率分布Figure 4 The curve of decay rate distribution of emitters ensembles

图5 辐射子簇的归一化衰减动力学曲线Figure 5 The curve of normalized decay dynamics of emitters ensembles

一般认为，赝带隙会对自发辐射有抑制作用，即当辐射子跃迁频率位于赝带隙中心时，其自发辐射比位于上、下带边时的慢. 但图4、图5 的结果表明，辐射子跃迁频率位于上带边时，其辐射寿命反而比位于赝带隙中心时的寿命长. 此结论与传统理论不符，可解释为，决定自发辐射寿命的因素是所有方向电磁模式数的总和，而非仅沿赝带隙方向的电磁模式数.

根据平均寿命的定义式(7)，可求出辐射子簇的平均寿命，其计算结果和实验结果［25］一致. 因此，本文定义自发辐射速率分布和衰减动力学函数，可有效地处理光子晶体中的自发辐射问题.

4 结论

本文针对木堆积结构光子晶体中不同位置的辐射子簇，计算了不同跃迁频率的自发辐射速率分布和衰减动力学.发现在木堆积结构中，即使折射率较低，也具有较宽的自发辐射速率分布，这说明木堆积结构有较强的光子晶体效应. 辐射子簇的衰减不再满足单指数衰减，本文定义了辐射子簇的衰减动力学函数，并计算了平均衰减寿命，其计算结果与文献的实验结果相吻合. 这些结果为实验探测辐射子簇的时间分辨衰减动力学和局域态密度提供了理论依据.

［1］YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics［J］. Phys Rev Lett，1987，58(20):2059 -2062.

［2］JOHN S. Strong localization of photons in certain disordered dielectric superlattices［J］. Phys Rev Lett，1987，58(23):2486 -2489.

［3］HO K M，CHAN C T，SOUKOULIS C M，et al. Photonic band gaps in three dimensions:New layer-by-layer periodic structures［J］. Solid State Commun，1994，89(5):413 -416.

［4］LIN S Y，FLEMING J G，HETHERINGTON D L，et al.A three-dimensional photonic crystal operating at infrared wavelengths［J］. Nature，1998，394(6690):251 -253.

［5］NODA S，TOMODA K，YAMAMOTO N，et al. Full three-dimensional photonic bandgap crystals at near-infrared wavelengths［J］. Science，2000，289(5479):604 -606.

［6］AOKI K，MIYAZAKI H T，HIRAYAMA H，et al. Microassembly of semiconductor three-dimensional photonic crystals［J］. Nat Mater，2003，2(2):117 -121.

［7］LI J，JIA B，ZHOU G，et al. Spectral redistribution in spontaneous emission from Quantum-Dot-Infiltrated 3D woodpile photonic crystals for telecommunications［J］.Adv Mater，2007，19(20):3276 -3280.

［8］GU M，JIA B，LI J，et al. Fabrication of three-dimensional photonic crystals in Quantum-Dot-based materials［J］. Laser Photonics Rev，2010，4(3):414 -431.

［9］TAKAHASHI S，SUZUKI K，OKANO M，et al. Direct creation of three-dimensional photonic crystals by a topdown approach［J］. Nat Mater，2009，8(9):721 -725.

［10］ISHIZAKI K，NODA S. Manipulation of photons at the surface of three-dimensional photonic crystals［J］. Nature，2009，460(7253):367 -370.

［11］VENTURA M J，GU M. Engineering spontaneous emission in a Quantum-Dot-doped polymer nanocomposite with three-dimensional photonic crystals［J］. Adv Mater，2008，20(7):1329 -1332.

［12］TANDAECHANURAT A，ISHIDA S，GUIMARD D，et al. Lasing oscillation in a three-dimensional photonic crystal nanocavity with a complete bandgap［J］. Nat Photon，2011，5(2):91 -94.

［13］WANG X H，WANG R，GU B Y，et al. Decay distribution of spontaneous emission from an assembly of atoms in photonic crystals with pseudogaps［J］. Phys Rev Lett，2002，88 (9):093902.

［14］ZHOU Y S，WANG X H，GU B Y，et al. Switching control of spontaneous emission by polarized atoms in two-dimensional photonic crystals［J］. Phys Rev Lett，2006，96(10):103601.

［15］BIROWOSUTO M D，SKIPETROV S E，VOS W L，et al. Observation of spatial fluctuations of the local density of states in random photonic media［J］. Phys Rev Lett，2010，105(1):013904.

［16］KRACHMALNICOFF V，CASTANIÉ E，WILDE Y D，et al. Fluctuations of the local density of states probe localized surface plasmons on disordered metal films［J］. Phys Rev Lett，2010，105(18):183901.

［17］LIU J F，JIANG H X，GAN Z S，et al. Lifetime distribution of spontaneous emission from emitter(s)in three-dimensional woodpile photonic crystals［J］. Opt Express，2011，19(12):11623 -11630.

［18］BUSCH K，JOHN S. Photonic band gap formation in certain self-organizing systems［J］. Phys Rev E，1998，58(3):3896.

［19］WANG R，WANG X H，GU B Y，et al. Local density of states in three-dimensional photonic crystals:Calculation and enhancement effects［J］. Phys Rev B，2003，67(15):155114.

［20］NIKOLAEV I S，VOS W L，KOENDERINK A F. Accurate calculation of the local density of optical states in inverse-opal photonic crystals［J］.J Opt Soc Am B，2009，26(5):987 -997.

［21］LIU J F，WANG X H. Spontaneous emission in microand nano-structures［J］.Front Phys China，2010，5(3):245 -259.

［22］VAN DRIEL A F，NIKOLAEV I S，VERGEER P，et al.Statistical analysis of time-resolved emission from ensembles of semiconductor quantum dots:Interpretation of exponential decay models［J］. Phys Rev B，2007，75(3):035329.

［23］MONKHORST H J，PACK J D. Special points for Brillouin-zone integrations［J］. Phys Rev B，1976，13(12):5188.

［24］LIU J F，JIANG H X，JIN C J，et al. Orientation-dependent local density of states in three-dimensional photonic crystals［J］. Phys Rev A，2012，85(1):015802.

［25］GAN Z，JIA B，LIU J F，et al. Enhancement of spontaneous emission in three-dimensional low refractive-index photonic crystals with designed defects［J］. Appl Phys Lett，2012，101(7):071109.