地下管线探测中隐蔽点精度检验公式的比较分析
2013-12-12田学军彭兴刚
王 乾,田学军,李 刚,彭兴刚
(1.中国冶金地质总局地球物理勘查院,河北保定071051;2.天津城建大学 地质与测绘学院,天津300384)
一、引 言
目前城市地下管线探测技术规程中关于隐蔽点精度的检验公式为《城市地下管线探测技术规程》CJJ61—2003(以下简称规程)条款 4.6.3,规定如下:
管线点的几何精度检查包括隐蔽管线点和明显管线点的检查。对隐蔽管线点应复查水平位置和埋深。对明显管线点应复查地下管线埋深。根据重复探测结果,按公式(1),(2)和(3)分别计算隐蔽管线点平面位置中误差mts和埋深中误差mth及明显管线点的量测埋深中误差mtd,mts和mth不得超过限差 δts、δth的0.5倍,限差 δts和δth按公式(4)和(5)计算。mtd不得超过±2.5cm

式中,Δsti为隐蔽管线点的平面位置偏差;Δhti为隐蔽管线点的埋深偏差;Δdti为明显管线点的埋深偏差;δts为隐蔽管线点重复探查平面位置限差;δth为隐蔽管线点重复探测埋深限差;n1隐蔽管线点检查点数;n2明显管线点检查点数;hi各检查点管线点中心埋深,当 hi<100 cm 是,取hi=100 计算[2]。
首先注意到:隐蔽点精度检验公式与埋深无关,是将隐蔽点的平面位置精度和埋深精度均视为等精度数据进行计算的;但是限差公式与埋深线性相关,按照误差原理,这两者明显矛盾,因为规程中采用的误差理论仍然基于最小二乘原理,又以两倍中误差做为限差(见总则1.0.3条款),但限差计算公式和中误差计算公式所得结果不是2倍关系,这显然错误。正因为如此,一部分长期从事管线探测与检验的单位提出来自己的隐蔽管线点精度检验公式,这些检验公式主要分为两类。
一类是以管线埋深为依据,将管线隐蔽点的检验公式分为几个埋深区间,各区间分别计算;另一类是通过误差理论推导,利用加权公式计算隐蔽管线点探测单位权中误差,以单位权中误差二倍作为限差。为下文讨论方便起见,分别称之为区间加权法和单位权法,将规程规定的方法简称为规程法。
二、3种地下管线隐蔽管线点精度检验公式
1.规程法
即采用规程直接给出的计算公式(1)、(2)、(4)、(5)直接计算。
2.区间加权法
区间法依据隐蔽点的埋深,将计算分为多个区间,一般为3 ~4 个区间,如区间分别为(0.0,1.0],(1.0,2.0],(2.0,mmax]或者(0.0,0.7],(0.7,1.4],(1.4,2.1],(2.1,mmax],各区间的限差以该区间的平均埋深为埋深,依据规程中的公式(1)和(2)计算其中误差,区间法以管线探测为例,其统计数据类似表1。

表1 区间加权法统计内容
3.单位权法
该方法以每米误差作为单位权误差,直接计算整个测区整体隐蔽点的单位权中误差,计算公式为

该方法可直接获取整个测区内隐蔽点探测的单位精度,相当于比例精度,更通俗的说是每米深度对应的误差。
三、3种方式的比较
规程法、区间加权法和单位权法3种方法,各有其特点和理论依据,在实际工作中,同一检验数据其统计结果不同。笔者从两个方面详细分析3种方法的优缺点。
1.误差统计原理分析
规程法的精度计算公式本质上是同精度观测计算公式,严格意义上只适用于各点探测精度相同的情况,但无论是管线探测的实际情况还是管线探测的精度规定都明确指出——隐蔽管线点探测精度与管线深度相关,所以隐蔽管线点探测是不等精度观测,故而该计算公式在误差理论上应用不太妥当,原理不相符合。对于限差计算公式虽然也采用的比例系数,以管线埋深为系数,但该系数无法区分埋深的离散程度,而离散程度是精度的主要特征,所以说该公式实际上无法准确衡量精度,其计算方法存疑。
区间加权法的精度计算公式不变,但限差计算公式使用区间加权。这在一定程度上区分了不同深度的贡献,但在这一具体区间内,其贡献值不能区分,如1.1 m埋深和1.9 m埋深贡献相同,仍然不合理。
单位权法与上述方法相比,优势明显,其精度计算公式采用加权系数,符合不等精度观测的原理,权系数的确定为埋深值,符合规程中关于管线探测精度与埋深线性相关的规定,计算的精度为单位权中误差,等同于我们通常的比例误差,更通俗的说法是每米的比例误差。这样一来,限差不用计算,根据规程总则关于两倍中误差为限差的规定,平面位置限差为0.10 h,故平面位置单位权中误差应不大于0.05 h,由于单位为1 m,故其值为0.05×1=0.05 m。同理,埋深限差为0.15 h,故埋深单位权中误差不得大于0.075×1=0.075 m。限差的计算简单明了,且对所有测区相同,实际上只要是执行规程规定的探测精度的所有项目,其限差均为平面单位权中误差0.050 m,埋深中误差0.075 m,无需计算。
2.数据试验比较与分析
数据试验分为两项:一项的目的在于检验3种计算公式对埋深与精度的关系的体现,另一项的目的在于检验3种方式对误差离散程度与精度的关系的体现。
在第1项试验中,笔者选取一组复探数据,样本量为30点,为了体现上述检验公式中精度与埋深的关系,该样本采用3组数据,一组为实测数据,另外一组将其埋深人为加大50 cm,第3组将其埋深在原值基础上人为减小50 cm,用以验证3种方式计算的结果是否与埋深相关。因篇幅限制试验数据从略,统计结果见表2。从表2中可以看到,采用规程法和区间加权法的统计的精度均与埋深无关,其平面和埋深中误差在3种不同的埋深条件下均无变化,这明显与事实及原理不符,单位权法在误差不变且埋深变大时,其单位中误差降低,说明比例精度提高,在误差不变但埋深变小时显示单位权中误差变大,说明比例精度降低,这与管线探测时,精度随着管线埋深变大而降低相一致。符合探测原理和实际情况。

表2 不同埋深相同误差统计结果
在第2项试验中,笔者选取了4组数据,在该项试验中,埋深不变,各点误差的总和∑Δd S值维持不变,1组为实测误差值,2组将误差的离散程度人为增大,即误差小于平均值的减去1 cm,误差大于平均值的加上1 cm;3组将离散程度人为减小,即误差小于平均值的加上1 cm,误差大于平均值的减去1 cm;4组的误差采用等比例计算,即将误差值按埋深等比例分配到各点。试验数据从略,统计结果见表3。

表3 相同埋深不同离散程度试验数据统计结果
从表3可以看出,规程法和区间加权法统计的中误差相同,对埋深均有体现,但对比例关系的体现错误,表现在随着平面偏差中误差虽然随着离散度的增大而增大、减小而减小,但在比例按埋深比例分配的最佳系数时,其计算的中误差值反而增大,这与实际不符。单位权法既随着离散度变化而变化,又在比例误差一致时达到最小,说明该计算方法既能够反应常规的误差离散情况,又能反应比例误差的优劣。
四、 单位权法理论推导
中误差是表征精度的一个绝对的数字指标,权是表征精度的相对数字指标。在不等精度观测和计算时,通过对不同精度的观测量赋予相应的权,可以客观衡量不等精度观测量的整体精度。在地下管线隐蔽管线点的探查工作中,可以通过单位权中误差的大小来衡量不同深度的地下管线隐蔽点探查的整体精度,根据地下管线隐蔽点的探测设备的电磁场工作原理和实际工作特点,笔者推荐以管线埋深的倒数的平方为观测量的权,以1 m埋深的探查精度为管线探查的单位权中误差,即令
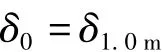
不同埋深的隐蔽管线点的探查值的权为

对于地下管线隐蔽管线点的精度检查,可以认为是进行了双观测,即两次观测,类似于往返测,设对不同埋深的隐蔽管线点各探查两次(探测时观测一次,复探时观测一次),得独立观测值为


即真值与其他本身之差为0。
现在对每个观测量进行了两次观测,由于观测值带有误差,因此每个值的差数一般是不等于零的,设

式中,di是第i个管线点位置或埋深的差数。既然已知各差数的真值应为零,因此di也就是各差数的真误差,即
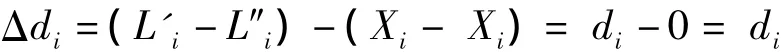
按权倒数传播率可得di的权倒数为

这样,就得到了n个差数的真误差和他们的权,由于管线点是有限数,由上式可知,单位权中误差为


有了单位权中误差m0可求得各探查值L'i和L″i的中误差为

如果所有的管线点埋深均相等,假设其埋深均为1.0 m,即此时
pi=1,则各探查点的中误差m为

此时,公式形式与当前规程中的规定相同,也与明显管线点量测和管线点测量质量评定公式形式相同,等精度观测是不等精度观测的特殊情况。
五、应用前景
在管线探测或管线探测监理工作中,经常需要检验和评定不同测区的管线探查精度,这包括两个方面,明显管线点的量测精度和隐蔽管线点的探查精度,前者为等精度观测,在不同测区其量测精度相同,其精度要求为一固定值,根据规程要求,期限差为5 cm,故其量测精度不能低于2.5 cm,与埋深无关。因此在执行规程的所有测区均执行这一标准统一,其精度统计为式(3)。
公式简单,计算方便,但对于隐蔽管线点,情况大为不同,原因在于,不同深度的管线探测精度不同,但采用规程法和区间加权法精度检验公式计算出的中误差与埋深无关,这等于说,埋深1 m探查误差10 cm,与埋深3 m探查误差10 cm精度相同。这样的推论导致任意两个测区无法比较隐蔽点的探查精度,因为不可能有两个测区的隐蔽管线点埋深相同——无论是整体相同或各个点均相同。实际上,由于规程的这一缺陷,的确导致多年来的管线探测精度比较工作难于开展,即使在理论层面也是如此,不但两个城市由于平均埋深不同而无法比较,同一城市即使是平均埋深接近,但各测区精度的离散程度不同,规程的精度检验公式仍然不能区分,在实际工作中造成诸多不便。区间法虽然能够通过加权,体现了不同区间的不同贡献,但过于粗略,与规程法区别不大。单位权法的优点在于,既能够区分不同埋深,又能够体现离散程度,还能够体现比例系数,同时可以不用计算限差,所有测区的限差均相同,其优势明显。
[1]中华人民共和国建设部.CJJ 61—2003城市地下管线探测技术规程[S].北京:中国建筑工业出版社,2003:17-18.
[2]盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,1994.
[3]张正禄,等.地下管线探测和管网信息系统[M].北京:测绘出版社,2007:73-74
[4]王友刚.城市地下管线普查探测的质量检验分析[J].测绘通报,2010(9):54-56.
[5]杨伯刚,张保刚.城市地下管线时空数据的组织与操作[J].测绘通报,2009(4):56-57.
[6]於宗俦,鲁林成.测量平差基础[M].北京:测绘出版社,1984:76-79.
[7]鲁林成,章书寿.大比例尺测图控制网必要精度的探讨[J].测绘学报,1963,6(3):15-18.
[8]武汉测绘科技大学测量平差教研室.测量平差基础[M].北京,测绘出版社,1996:16-32.
