基于等效Q值的反Q滤波影响因素分析

李雪英，裴江云，张惠瑜，吴 鹏，刘心宇

（1.东北石油大学 地球科学学院，黑龙江 大庆 163318； 2.大庆油田博士后科研工作站，黑龙江 大庆 163458； 3.东北石油大学 博士后科研流动站，黑龙江 大庆 163318； 4.大庆油田有限责任公司 勘探开发研究院，黑龙江 大庆

163712； 5.中国石油青海油田公司勘探开发研究院，甘肃敦煌 736202； 6.大庆油田有限责任公司第二采油厂，黑龙江 大庆 163416； 7.大庆油田有限责任公司，第三采油厂，黑龙江 大庆 163113）

0 引言

反Q滤波是一种比较成熟的叠后提高地震资料深层分辨率的技术手段.反Q滤波是由Hale D[1]提出的，以Futterman W I提出的数学模型为基础，采用级数展开方法作近似高频补偿[2].Robinson J C提出的反Q滤波方法对速度频散导致的相位畸变进行合理校正[3]，但是忽略能量损失导致的振幅衰减.Bickel S H等[4]根据Srtick E[5]提出的数学模型进行反Q滤波处理，实际应用效果很好，由于它是基于积分算法的，计算效率很低.Hargreaves N D等提出一种基于傅氏变换的反Q滤波算法[6]，可有效校正常Q介质导致的相位畸变，但无法恢复地震子波的振幅衰减.基于地震波场延拓理论，Wang Yanghua提出适用于水平层状介质，并且可以同时完成振幅补偿及相位校正的稳定反Q滤波算法[7]，将振幅补偿项写成两个关于时间和频率的一元函数的乘积，以波场延拓理论和FFT算法为基础，具有很高的计算效率；后又将它推广到Q值随时间或深度连续变化的情况[8].

虽然已经发展基于波场延拓理论的层状Q值的反Q滤波方法，但是利用地面地震资料直接进行层状Q值建模存在困难，精度较差[9－10]，使层状反Q滤波技术的应用受到一定的限制.笔者给出基于等效Q值的反Q滤波算法，分析其影响因素.

1 基于等效Q值的反Q滤波方法

1.1 基本原理

反Q滤波是地震波场的逆向传播过程[11－19].基于波场延拓理论，对于水平层状黏性介质，设z轴垂直向下，并且每一个水平均匀介质层的厚度为Δz，则反Q滤波波场延拓公式[20－21]为

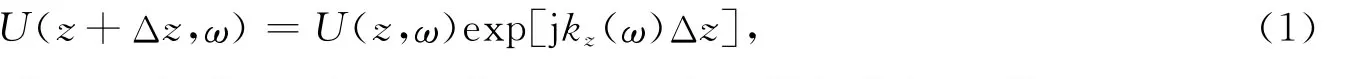
式中：U（z，ω）为深度z的平面波场；ω为角频率；j为虚数单位；kz（ω）为空间角频率，并且

将式（2）代入式（1），令Δτ＝Δz／vi，旅行时间，得到：

其中2个e指数项分别为相位补偿项和振幅补偿项.

考虑地层Q模型Q（τ）为垂直时间的一维函数，将地表波场（τ＝0）向下延拓到时间τ为

定义等效Q值，即Qeff为

由式（5）可以看出，Qeff是随时间连续变化的，将式（5）代入式（4），得到频域内基于等效Q值的反Q滤波算法为

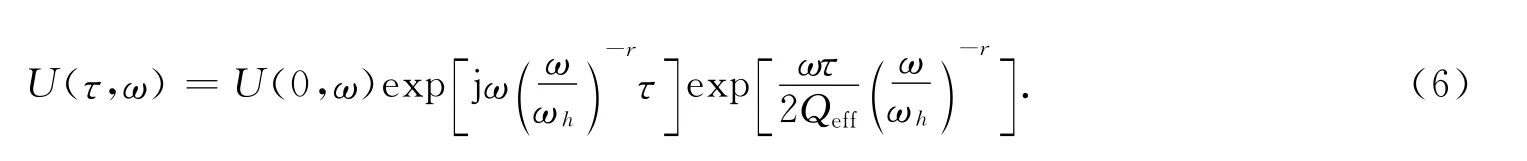
1.2 稳定性控制

为了使噪声在补偿过程中不出现不必要的扩大，设计一个适用于高频的反Q滤波补偿算子，采用一种适用于高频的稳定性控制策略：在频域内重新构造一个以自变量为的补偿算子函数Γ（χ），设定截止值χc（由幅度控制门限阈值Glim计算得到），当χ≤χc时，补偿函数为精确的反Q补偿算子谱；当χ＞χc时，利用一个一阶光滑可导的衰减e指数改造补偿算子谱，使其光滑地衰减为一个很小的正常数.令，则稳定性控制为

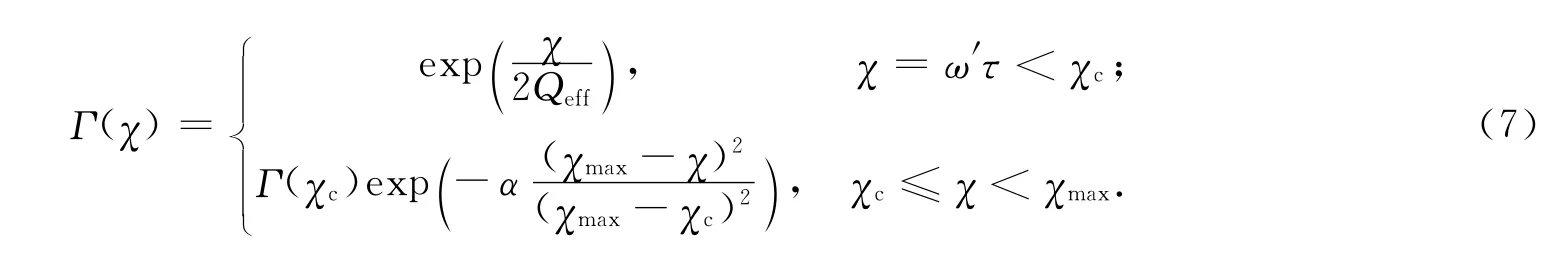
式中：α为一很小的正常数，一般取10－4.加入新的稳定性控制方法后，式（6）变为

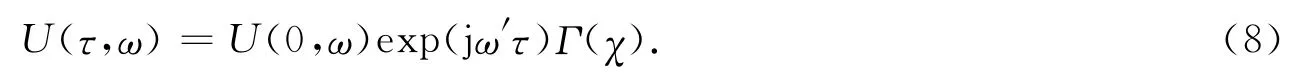
把补偿后的频率域数据反变换到时间域，得到经过反Q滤波补偿后的时间域地震数据为

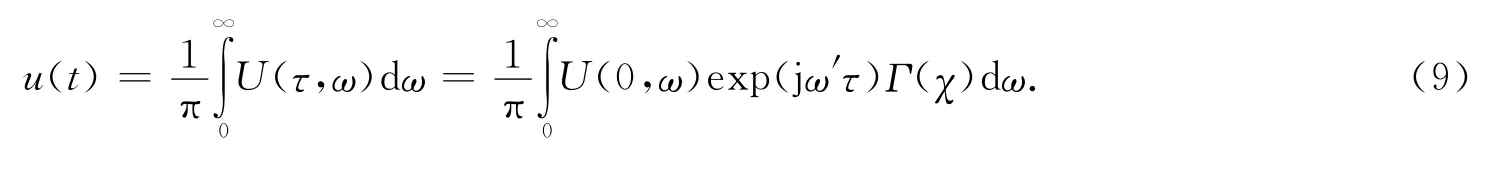
2 影响因素

采用波动方程正演模拟具有3个地层界面（界面位置分别在1、2、3s处）的理论合成数据，其中震源子波的主频为30Hz，介质速度为2 000m／s，Q值为50，地震记录的采样点个数为2 000，采样间隔为2 ms；然后分别从信噪比、等效Q值精度、调谐频率、门限阈值等方面，研究基于等效Q值的反Q滤波技术的主要影响因素.

2.1 信噪比

实际地震数据中包含不同程度的随机噪声，而地震道中的随机噪声对补偿效果产生影响.加入不同信噪比的随机噪声黏性补偿后的地震道见图1.由图1可知，噪声越大，稳定性问题越难控制，补偿效果越不好，要求在反Q滤波之前应合理地压制噪声.

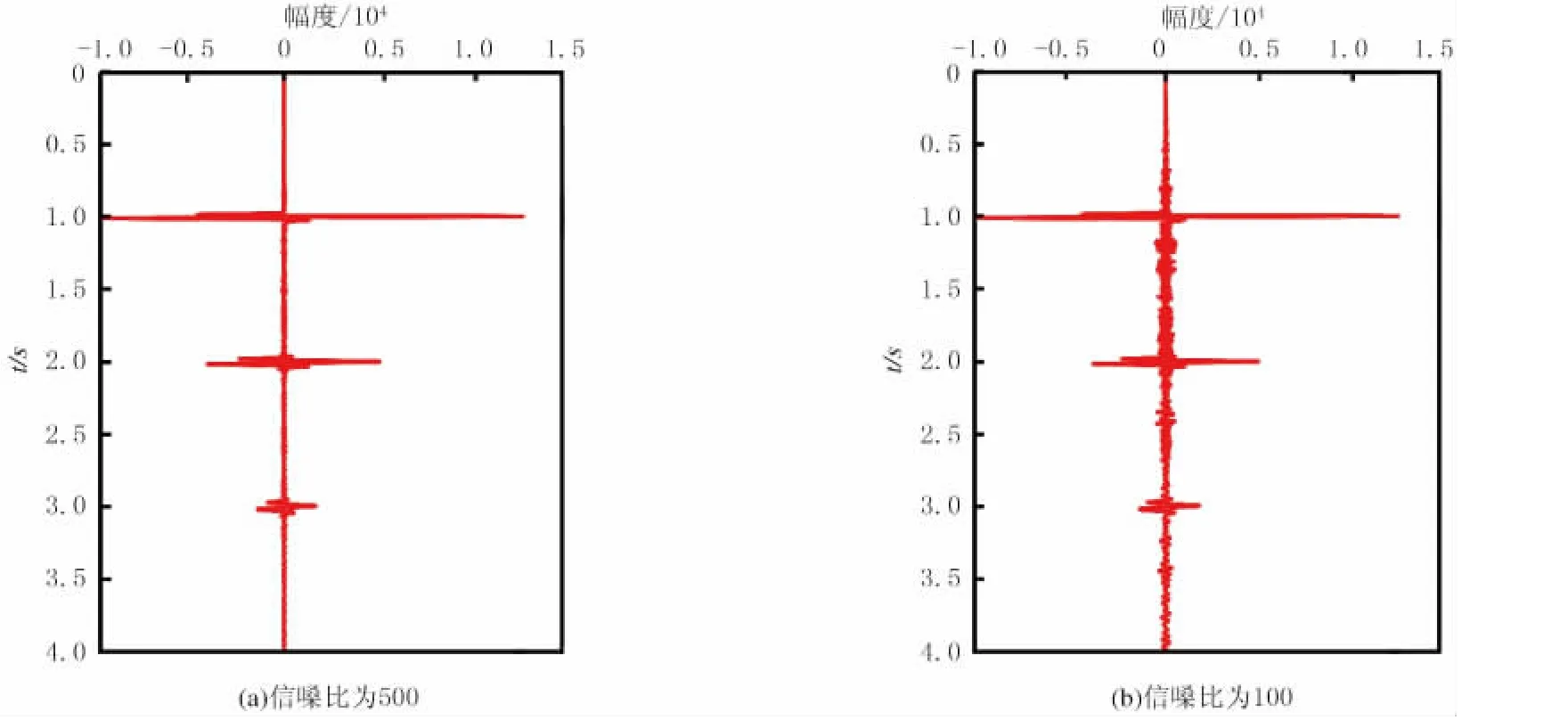
图1 不同信嗓比补偿后地震道随机噪声的影响Fig.1 Influence of random noise

在理论上，对于含有噪声的地震道，地震子波在向下传播过程中能量逐步衰减，超出一定距离后，信号的能量衰减到噪声水平以下，此时对信号振幅的恢复将造成噪声的过度放大，使有效信号堙没在噪声中.因此，平均噪声能量以下的有效信号能量在原则上是不可恢复的.

2.2 等效Q值精度

以正演模拟得到的黏性吸收地震道为研究基础，选取不同的等效Q值，用基于等效Q值的反Q滤波方法对它进行补偿；通过广义S变换获取3个地层界面处的局部频谱，与正确Q值的补偿作比较，观察补偿效果的变化.

当选取的等效Q值为40时，第二个地层界面出现过补偿，由于存在稳定性控制，使得高频成分得不到有效恢复，造成第三层的峰值频率有所降低（见图2（a），其中实线代表第一个地层界面的局部傅利叶谱，虚线为第二个界面的，点线为第三个界面的）；当选取的等效Q值为50时，第二、三层峰值频率与第一层的峰值频率特征基本一致，第三层的峰值频率略低是由稳定性控制造成的（见图2（b））；当选取的等效Q值为80时，出现补偿不足（见图2（c））.因此，只有等效Q值选择正确，基于等效Q值的反Q滤波才能取得良好的补偿效果.

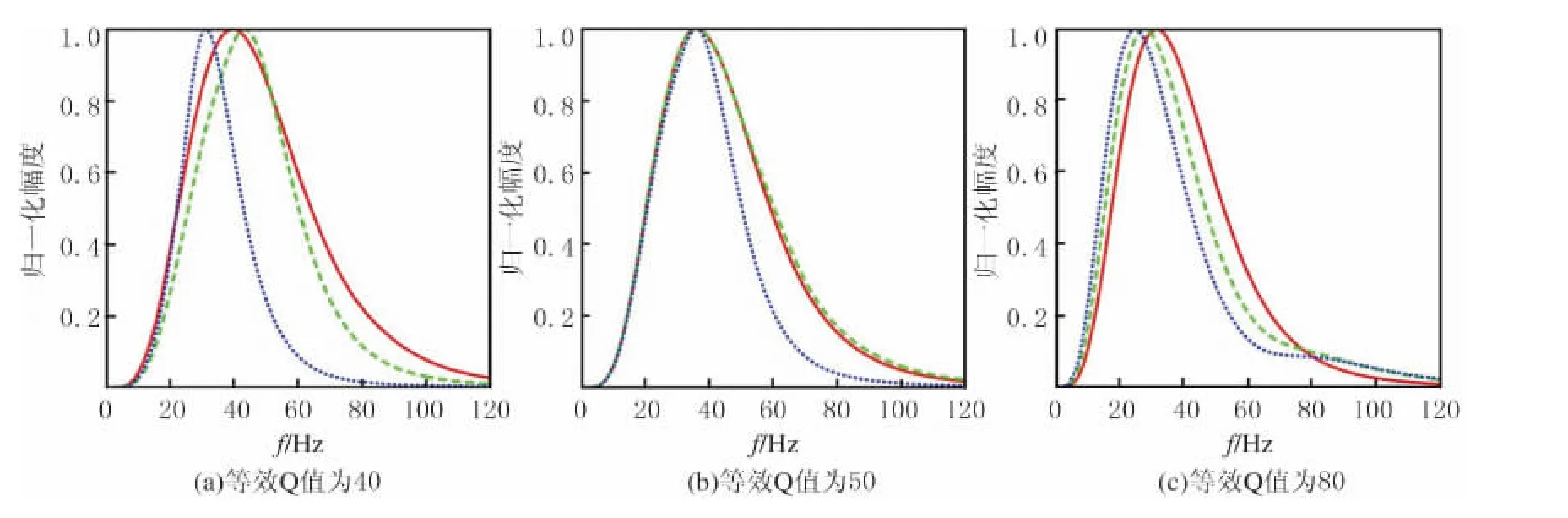
图2 不同等效Q值补偿后地震道精度的影响Fig.2 Influence of effective quality factor precision

2.3 调谐参数

由式（6）可知，调谐参数直接影响反Q滤波补偿后的相位谱，因此选择不同的调谐参数，将影响补偿后的地震子波的到时.分别选取最高截止频率和峰值频率作为调谐参数，对同一地震道黏性地震数据进行反Q滤波补偿，两道合并后将2s处放大后发现，选择最高截止频率比选择峰值频率的相位补偿效果更好，更接近无黏性吸收时的地震波的相位，走时更加准确（见图3，其中实线代表峰值频率，虚线代表最高截止频率）.

2.4 门限阈值

门限阈值直接影响稳定性控制的效果，选取不同门限阈值对黏性地震数据进行反Q滤波的结果见图4.由图4可知：当门限阈值取200时，第三个界面的地震子波分辨率改善不明显，振幅补偿弱；当门限阈值取2.0×104时，虽然振幅得到有效恢复，分辨率明显提高，但是底部出现不稳定现象，说明门限阈值选取越大，振幅补偿越大，但也增加算法的不稳定性.

图3 不同频率补偿后地震道调谐频率的影响Fig.3 Influence of tune frequency

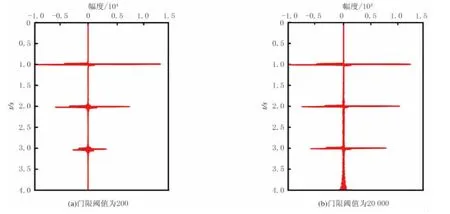
图4 不同门限阈值补偿后地震道的影响Fig.4 Influence of gain limit

3 结论

（1）分析基于等效Q值的反Q滤波补偿效果的影响因素，噪声越大，信噪比越低，稳定性问题越难控制，补偿效果越不好，应在反Q滤波前合理地压制噪声.

（2）等效Q值选取精度对反Q滤波的振幅恢复有很大影响，对相位补偿无影响，等效Q值选取偏小，补偿过大；等效Q值选取偏大，补偿不足.

（3）选择最高截止频率比选择峰值频率的相位校正效果更好，走时更加准确.

（4）门限阈值越大，振幅补偿越大，补偿后振幅越接近无黏性吸收的情况，但也增加算法的不稳定性.

[1]Hale D.An inverse Q－filter[A].Standford Exploration Project[C].1981，28：289－298.

[2]Futterman W I.Dispersive body waves[J].Journal of Geophysics Research，1962，67（13）：5279－5291.

[3]Robinson J C.A technique for the continuous representation of dispersion in seismic data[J].Geophysics，1979，44（5）：1345－1351.

[4]Bickel S H，Natarajan R R.Plane－wave Q deconvolution[J].Geophysics，1985，50（9）：1426－1439.

[5]Strick E.A predicted pedestal effect for pulse propagation in constant－Q solids[J].Geophysics，1970，35：387－403.

[6]Hargreaves N D，Calvert A J.Inverse Q filtering by Fourier transform [J].Geophysics，1991，56：519－527.

[7]Wang Y H.A stable and efficient approach of inverse Q filtering[J].Geophysics，2002，67（2）：657－663.

[8]Wang Y H.Inverse Q filter for seismic resolution enhancement[J].Geophysics，2006，71（3）：V51－V60.

[9]李雪英，孙丹，井涌泉，等.利用广义S变换进行等效 Q值扫描分析[J].地球物理学进展，2009，24（5）：1696－1702.Li Xueying，Sun Dan，Jing Yongquan，et al.Scanning analysis of effective Q using generalized S transform.Progress in Geophysics，2009，24（5）：1696－1702.

[10]杜增利，施泽进，田军，等.新疆沙漠地区低降速带品质因子计算[J].大庆石油学院学报，2006，30（6）：20－23.Du Zengli，Shi Zejin，Tian Jun，et al.Calculation of quality factor of LVL in Tarim basin[J].Journal of Daqing Petroleum Institute，2006，30（6）：20－23.

[11]裴江云，何樵登.基于 Kjartansson模型的反 Q滤波[J].地球物理学进展，1994，9（2）：90－99.Pei Jiangyun，He Qiaodeng.Inverse Q filtering according to Kjartansson model[J].Progress in Geophysics，1994，9（2）：90－99.

[12]马昭军，刘洋.地震波衰减反演研究综述[J].地球物理学进展，2005，20（4）：1074－1082.Ma Zhaojun，Liu Yang.A summary of research on seismic attenuation[J].Progress in Geophysics，2005，20（4）：1074－1082.

[13]徐平，王宝善，张尉，等.利用互相关函数求地震波衰减[J].地球物理学报，2006，49（6）：1738－1744.Xu Ping，Wang Baoshan，Zhang Wei，et.al.Estimating seismic attenuation using crosscorrelation function[J].Chinese Journal of Geophysics，2006，49（6）：1738－1744.

[14]姚振兴，高星，李维新.用于深度域地震剖面衰减与频散补偿的反Q滤波方法[J].地球物理学报，2003，46（2）：229－233.Yao Zhenxing，Gao Xing，Li Weixing.The forward Q method for compensation attenuation and frequency dispersion used in the seismic profile of depth domain[J].Chinese Journal of Geophysics，2003，46（2）：229－233.

[15]李振春，王清振.地震波衰减机理及能量补偿研究综述[J].地球物理学进展，2007，22（4）：1147－1152.Li Zhenchun，Wang Qingzhen.A review of research on mechanism of seismic attenuation and energy compensation[J].Progress in Geophysics，2007，22（4）：1147－1152.

[16]王珺，杨长春，乔玉雷.用稳定高效的反Q滤波技术提高地震资料分辨率[J].地球物理学进展，2008，23（2）：456－463.Wang Jun，Yang Changchun，Qiao Yulei.Improve the seismic resolution with a stable and efficient inverse Q filter[J].Progress in Geophysics，2008，23（2）：456－463.

[17]王建民，陈树民，苏茂鑫，等.近地表高频补偿技术在三维地震勘探中的应用研究[J].地球物理学报，2007，50（6）：1837－1843.Wang Jianming，Chen Shuming，Su Maoxin，et al.A study of the near surface high frequency compensation technology in 3Dseismic exploration[J].Chinese Journal of Geophysics，2007，50（6）：1837－1843.

[18]张凤军，吕延防.地震老资料连片高分辨率处理方法[J].大庆石油学院学报，2004，28（1）：7－9.Zhang Fengjun，Lv Yanfang.High resolution integrated processing methods for chronological seismic data[J].Journal of Daqing Petroleum Institute，2004，28（1）：7－9.

[19]马世忠，王子文，赵德斌，等.高分辨率地震勘探在泰康地区储层横向追踪及薄层定量预测中的应用[J].大庆石油学院学报，1993，17（3）：107－111.Ma Shizhong，Wang Ziwen，Zhao Debin，et al.Reservoir lateral correlation and prediction in quantity for thin bed with high resoluable seismic data in TK area[J].Journal of Daqing Petroleum Institute，1993，17（3）：107－111.

[20]李雪英，吕喜滨.稳定有效的频域反 Q滤波方法[J].科学技术与工程，2011，10（25）：6257－6260.Li Xueying，Lv Xibin.A stable and efficient approach of inverse Q filtering in the frequency domain[J].Science Technology and Engineering，2011，10（25）：6257－6260.

[21]李雪英，吕喜滨.稳定高效的时域反 Q滤波方法[J].地球物理学进展，2010，25（1）：211－218.Li Xueying，Lv Xibin.A stable and efficient approach of inverse Q filtering in time domain[J].Progress in Geophysics（in Chinese），2010，25（1）：211－218.