改进的人工鱼群算法在试题库构建中的应用*
2013-12-10李晓静
李晓静,李 攀
(1.济源职业技术学院艺术设计系,河南 济源459000;2.济源职业技术学院信息工程系,河南 济源459000)
引言
随着计算机和现代教育理念的蓬勃发展,基于Web 的信息系统应用越来越广泛,利用网络考试系统取代纸质考试是近几年来的一个研究领域.在高等院校中,作为检验学生知识和技能掌握情况的主要考核方式之一的纸质考试,由于其过程复杂、效率低下并且较易出错,渐渐地不能适应高等院校发展的需要,而基于Web 的网络考试系统具有方便、灵活、节省成本、高效率等优势,使其在高等院校的应用中显得越来越普遍.
使用网络考试系统,教师平时可以有效地收集试题并保存到试题库中,考试时的出卷将变得较为轻松,甚至可以完全由计算机自动进行;利用计算机能科学的分析学生的成绩情况和教学中的不足环节.利用试题库技术可以充分地实现考教分离,提高办学效益.
1 试题库组卷策略
试题库属性参数的设置与自动组卷策略是网络在线考试系统建设中最关键的两个环节.要完成组卷过程,就要求系统根据组卷策略输入的属性和参数设置抽取出所要求的试题[1].在构建组卷策略时,要考虑三方面的内容,即试题属性项目的定义、试题组卷参数的定义和试题变换算法的说明,其中要充分考虑试题查询参数的定义和对所定义的参数使用的算法等.
试题库自动组卷需要设置试题的一些属性,如:难度系数、区分度、题目分值等,根据属性和组卷策略自动生成试卷.具体步骤如图1 所示.
2 人工鱼群算法描述
通过对鱼群集体合作寻食行为的分析,李晓磊等人于2002年提出了一种新型的寻优算法,即人工鱼 群 算 法 (Antificial Fish Swarm Algorithm,AFSA)[2],该算法模拟出鱼群之间相互协作提高群体效益的方法.
AFSA 算法中有多条“人工鱼”共同存在,集体合作寻优,这种行为类似于鱼群寻找食物,其中一条“人工鱼”代表了AFSA 中的一个备选解.设定有一个包含n 条人工鱼的群体所构成的目标搜索空间中,定义向量为第i 条人工鱼的状态,那么每条人工鱼的状态就是该目标搜索空间的一个潜在解,即欲寻优的变量,记作:Xi=(xi1,xi2,…,xin)(i =1,2,…n).Xi值优劣的衡量取决于函数值的大小,该函数值的计算可通过将所得到的潜在解Xi带入被优化的函数,以所得到的最小值为最优值.简而言之,就是将一群人工鱼(随机解)作为AFSA 的初始化状态,这些人工鱼通过觅食行为、聚群行为、追尾行为在迭代优化函数过程中,逐步更新自己,生成新鱼群,从而实现全局最优.
以上所描述的人工鱼群算法模型中,每条人工鱼为了从觅食、聚群和追尾中选择一种行为实际执行,就要探索它当前所处的环境和伙伴的状况,当寻找到最优的解时,人工鱼将会集结在几个局部极值周围.在通常情况下,求最优解时,为了更方便获取全局极值域,会将适应值较大的人工鱼集结于值较大的极值区域周围.作为一种新型的高效寻优算法,该算法的收敛速度不但快,而且还可以有效地解决实时性问题;特别是在精度要求不太高的情况下,使用该算法可以更快地找到解决方法.该算法模型如下所示:

3 试题抽取算法中对人工鱼群算法的约定
3.1 试题样本空间及个体距离的约定
在网络在线考试系统中,将要抽取的试题方案表示为鱼群的单个个体.假如在考试系统中有四道题,分别为:第一题、第二题、第三题和第四题,那么在抽取题目的过程中,搜索空间中的状态1100 表示抽取第一题和第二题,而不是抽取第三题和第四题;在搜索空间中,每个状态都能表示一个个体,每两个个体之间的距离就是这两个状态之间差异的程度,比如一个个体状态是0101,另一个个体状态是0011,那么这两个状态之间共有2 位不同,也就是说它们之间的距离是2.
3.2 人工鱼食物浓度的计算
任一状态的食物浓度计算公式如下:
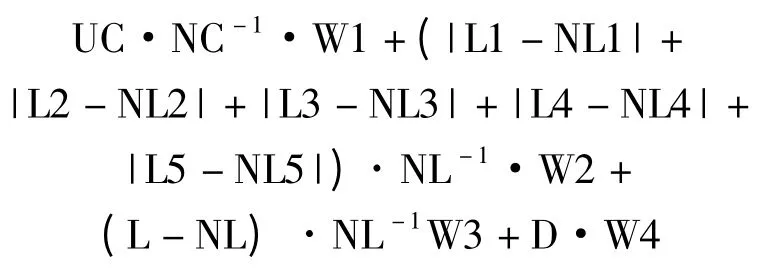
在该公式中,将需覆盖而未覆盖的叶子知识点数量记为UC;将考试范围内叶子知识点总量记为NC;并依据试题的难易程度(困难、较困难、普通、较简单、简单)将分值依次记为L1 至L5;依据教师规定题目的难易程度(困难、较困难、普通、较简单、简单)将分值记为NL1 至NL5;则有L =L1 +L2 +L3+L4 +L5;NL=NL1 +NL2 +NL3 +NL4 +NL5;D 表示该试题的区分度;W1、W2、W3和W4 分别表示在搜索过程中知识点覆盖率、难度差异、总分差异和区分度的重要程度,默认比例是1∶ 1∶ 1∶ 1.由上式不难看出在这里适应度函数值是越小越好[3].
3.3 人工鱼行为约定
当人工鱼搜索行为开始后,首先在其视野内随机选择一个状态,产生一个鱼群,鱼群中的个体随机产生.种群数量确定后,进行追尾行动,每条鱼Xi能查看到距离小于Visual(Visual为可视域)的其他鱼(可根据搜索空间指定),在这里将最小适应函数值记为Xj,将适应度函数值记为Yj,并用nf表示最小适应函数值Xj可视区域内的人工鱼数量,当Yj·nf<δ·Yi(δ 表示拥挤度因子,此处取1)时,表示当前最小适应函数值周围“食物”较多且不太拥挤,这时就要对比Xi、Xj的值,并对不相同的位重新取值(比如Xi是1010,Xj是0011,则要对Xi的第1 位和第4位重新随机取值),从而使Xi的值趋向于Xj[4].在追尾行为不成功的情况下,就要重新执行聚群活动,为了重新形成一个鱼群,每条人工鱼都要在可视区域内找到其它鱼,并且确定鱼群的中心点,方法是:假如鱼群中有一半的鱼第i 位值为1,那么鱼群中心点的第i 位值也为1,否则就为0,接着再次进行追尾活动,采用前面的方法检测中心点周围的“食物”数量和拥挤程度,并据此决定是否进行聚群行为[5].假如不能进行聚群行为,则要重新进行觅食行为,“人工鱼”随机选取自身的Visual 个位,通过随机变换得到一个新的状态,假如所得到的新状态比原状态优越,则趋向于新状态,否则就要再次进行觅食行为,如果重复觅食行为m 次后仍然没有找到更好的状态,“人工鱼”就要进行随机运动(m 值由搜索空间决定)[6].
4 海量试题抽取的算法改进,基于AFCM 的试题抽取
运用上面所述的人工鱼群算法进行试题抽取,在试题库的题量较少的情况下效率较高,但在海量题库的情况下性能就明显降低了.为了解决这个问题,我们尝试引入基于人工鱼群的模糊C 均值(Fuzzy C-means,FCM)的改进算法(AFCM).其基本思想如下:
将题库中所有试题作为AFCM 的样本空间,首先对所有试题按要求进行归类(寻找聚类中心),归类的原则可以是试题难度、知识点分布、区分度等,也可以是几者的结合.经过归类,可以将试题按预设规则划分成不同的子集,然后在已经优化的局部试题集的基础上再一次执行人工鱼群抽取算法.这样可以将全局的试题抽取转化为局部的最优抽取,可以有效地提高海量试题抽取的效率.
5 结论
根据试题库建模理论,结合对各种试题抽取算法的实践与研究,通过使用AFCM和人工鱼群算法相结合的方法,对海量试题抽取时的效率进行了改进,取得了很好的效果.在实践中,运用软件工程的思想,采用微软.NET 平台的C#语言和ASP.NET 技术,实现了基于WEB 的在线综合考试系统,整个系统采用三层B/S 架构实现,后台数据库端采用了SQL 分布式视图的技术以提高数据访问的性能,前台采用基于JQUERY和WEB 服务的AJAX 技术提供无刷新界面以提高用户体验.同时,我们模拟构造了大试题量的试题库,经过运行实验,在WEB 环境下对试题的抽取性能有很大的提高,基本上达到了我们的目的.目前,我们正在对基于人工鱼群的FCM 算法和人工鱼群算法进行深层结合,使之在大批量试题的抽取上性能更加提高,更具应用价值.
[1]肖洋,王强,刘凤新.在线考试组卷算法研究[J].北京化工大学学报,2006,33(4):44-47.
[2]李晓磊.一种新型的智能优化方法—人工鱼群算法[D].杭州:浙江大学,2003.
[3]陈磊,姜薇.通用考试系统的设计与实现[J].计算机工程与设计,2007,28 (17):4285-4288.
[4]欧丽辉.基于远程教育的网络考试的设计与构想[J].中小企业管理与科技,2011,(7):279-280.
[5]李晓磊,路飞,田国会.组合优化问题的人工鱼群算法应用[J].山东大学学报:工学版,2004,34(5):64-67.
[6]高尚,杨静宇.群智能算法及其应用[M].北京:中国水利水电出版社,2006.
