基于SVM回归方法的风速预测研究
2013-12-1095853部队宋建丽
95853部队 赵 斌 宋建丽
1.引言
风电场机组一直受无规律的变向、变负荷的风力作用,这会使发电机的发电量波动很大,对电网造成较大的威胁,因此对风电场风速预测的理论和实际的研究具有重要意义。支持向量机(SVM)在国外已经应用在话者识别[1]、生物医学[2]、噪音处理[3]等方面,在国内虽然也在模式识别、机械故障诊断、电力预测方面有应用,但是在风电场风速预测上应用较少[4]。风速受气压、温度、纬度、海拔等的影响,风速的随机性很强,本文利用SVM预测风速,百分比误差精度在5%以内,可以为风电场风速预测提供较好的参考。
2.支持向量机回归原理
1963年,Vapnik提出一种非常有潜力的分类方法支持向量机(Support Vector Machine,SVM),它是一种基于统计学习理论的模式识别方法[5]。SVM以训练误差作为优化问题的约束条件,以置信范围值最小化作为优化目标,成功的解决了小样本、非线性及高维模式识别问题,并能够推广应用到函数拟合等其他机器学习问题中。

表1 风速实际值与预测值之间的比较
支持向量机回归的主要思想是通过一个非线性映射Φ,将数据x映射到高位特征空间F,并在这个空间进行线性回归[6]。
已知一个训练集

以及假设函数集

其中权值nw∈R ,而b∈R为阈值。
回归支持向量机一般可以表示为下面的规划问题:
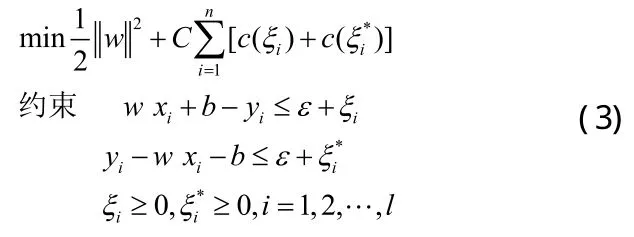
其中,iξ和为松弛变量,c()ξ是损失函数,C为惩罚项常数。

图2 某风电场天平均风速
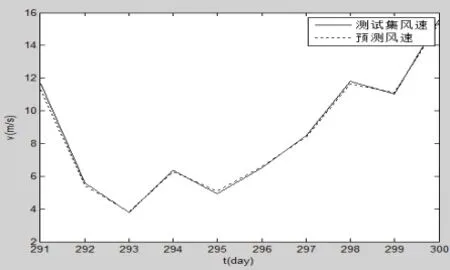
图3 风速实际值与预测值
常用的核函数如下[9]。
1)多项式核:K( x, xi)=(x, xi+1)d,d为阶数;
3)感知器核:K( x, xi)=tanh(βxi+b)。
本文在风速预测中采用的核函数K( x, xi)为径向基RBF核函数(高斯核函数)。
3.SVM参数选择和优化
由于选择的是RBF核函数,所以在核函数参数的选择上有惩罚项常数C和RBF的参数g。目前参数寻优方法有网格寻优,GA寻优,PSO寻优等,其中最简单最有效的方法是网格寻优。但是上述几种方法都是基于知道测试集标签的情况下进行参数优化的,本文是在假定不知道测试集标签的情况下,运用交叉验证(Cross Validation)的方法找到最佳的C和g。
C和g的值是在以2为底的[-8,8]上取值,即C和g的值是在[2-8,28]取值,取最终测试集数据和预测集数据误差最小的C和g。
4.实验与分析
本文选取我国某风电厂的风速数据,风速数据为一天中风速的平均值。本文选取某年当中连续300天的风速数据作为样本,前290个作为训练集,后10个作为预测集。实验程序是在MATLAB 7.11(R2010b)平台上完成,通过对比实测值和预测值来判断预测的精度。本文风速预测的步骤如图1所示。
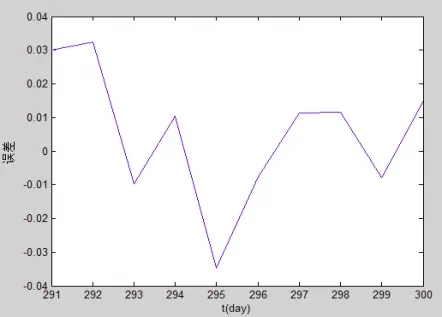
图4 风速实际值与预测值之间误差
对实验数据预处理,即用MATLAB自带的mapmaxmin归一化到[-1,1],构成训练集,然后参数寻优选择合理的核函数,建立预测模型,最后进行真实数据和预测数据的误差分析。支持向量机预测模型效果一般用误差百分比(APE)、平均百分比误差(MAPE)和平均绝对误差(MAE)来评价[7-8],APE、MAPE和MAE的表达式如下:

式中Rt代表时间t实际测量值real data,Pt代表时间t预测值predict data,n代表时间点的个数。根据取得的数据,图2给出风电场天平均风速。
由图2可以看出风速在300天中随机性很大,从1.460m/s~29.580m/s,平均风速为11.362m/s。本文选择RBF为核函数,其参数数目较少,而且容易建立模型,并确定参数:惩罚因子C=2,gamma函数g=1.1,e-SVR中损失函数p=0.01。
风速预测值与实际值的对比如图3。实线代表实际风速,虚线代表预测风速。由图可以看出预测效果还是不错的。图4为风速实际值与预测值之间的误差图。
根据实际风速和预测风速值得到表1。
由表1可见,风速实际值与预测值的比较,平均百分比误差(MAPE)为1.705%,平均绝对误差(MAE)为0.1705,误差百分比误差最大的不超过5%,预测效果可以达到预测精度,验证了SVM理论在风速预测中的可行性。
5.结语
本文结合风场部分风速资料,利用SVM建立风速预测模型,核函数取RBF核函数是为了建模方便,惩罚因子C,gamma因子g,e-SVR中损失函数p的选取是利用libsvm工具箱中SVMcgForRegress求得,模型中数据的平均百分比误差(MAPE)为1.705%,平均绝对误差(MAE)为0.1705,较为理想,可以为风电场的风速预测提供较有价值的参考。
[1]Campbell,W.M.A SVM/HMM system for speaker recognition[J].IEEE international Conference on Acoustics,Speech and Signal Processing-Proceedings,2003:209-212.
[2]Rémi Cuingnet,Charlotte Rosso,Marie Chupin,Stéphane Lehéricy,etc.Spatial regularization of SVM for the detection of diffusion alterations associated with stroke outcome[J].Medical Image Analysis,2004,5(15):729-737.
[3]R Kumar,A Kulkarni,V.K Jayaraman,B.D Kulkarni.Symbolization assisted SVM classifier for noisy data[J].Pattern Recognition Letters,2004,4(25):495-504.
[4]杜颖,卢继平,李青,邓颖玲.基于最小二乘支持向量机的风电场短期风速预测[J].电网技术,2008,32(15):62-66.
[5]Corinna Cortes,V.VAPNIK.Support-Vector Network[J].Machine Learning,1995,20(3).
[6]韩立群.人工神经网络理论、设计及应用(第二版)[M].北京:化学工业出版社,2007.
[7]张华,曾杰.基于支持向量机的风速预测模型研究[J].太阳能学报,2010,31(7):928-932.
[8]彭怀午,杨晓峰,刘方锐.基于SVM方法的风电场短期风速预测[J].电网与清洁能源,2009,25(7):48-52.
[9]Johan A.K.Suykens,Tony Van Gestel,Jos De Brabanter,Bart De Moor,Joos Vandewalle.Least Squares Support Vector Machines[M].Singapore:World Scientific Publishing Co.Pte.Ltd,2002.51-54.
