基于蒙特卡洛的发动机推力线横移数值仿真
2013-12-10张万里
房 雷,张万里
(1中国空空导弹研究院,河南洛阳 471009;2航空制导武器航空科技重点实验室,河南洛阳 471009)
0 引言
固体火箭发动机的零部件在加工、装配过程中,会产生尺寸和形位公差;在发动机工作过程中,存在燃烧、燃气流动以及喷管烧蚀的不均匀性,这些因素都不可避免的造成发动机推力与弹轴形成偏移和夹角,影响导弹控制精度或火箭弹射程、横偏[1]。
由于燃烧、燃气流动以及喷管烧蚀的不均匀性难以控制和测量,目前在工程中一般都对上述因素进行简化,采用喷管扩张段轴线与发动机轴线的平移和夹角来表征推力线横移与偏斜,通过测量相关几何参数,计算得到横移与偏斜的具体结果。张春富[2]提出了一种激光跟踪仪测量发动机推力线的方法;来平安[3]在实测数据的基础上,建立了一种推力线横移和偏斜的模拟计算方法。
如果在发动机设计阶段即得到横移与偏斜的大小,对于优化结构设计、合理分配零部件之间的公差、提高零件的加工工艺性有重要的意义。
发动机推力线横移一般由零部件的同轴度误差和装配间隙造成,对推力线横移的研究,可转化为对发动机燃烧室和喷管等零部件公差设计的研究。传统的公差设计有两种方法,极值法和概率法[4],由于零件尺寸公差和装配方向在实际生产中都是随机分布的,如果采用极值法进行推力线横移分析,不能反映实际横移大小,很可能造成设计不满足指标要求的结果,从而需要提高设计精度,造成加工成本增加。
文中采用极坐标法建立推力线横移的数学模型,并用蒙特卡洛法进行统计计算,在完成设计后即可得到推力线横移的统计分析结果,为评估、优化发动机结构设计、降低零件加工成本提供了依据。
1 数学模型
1.1 影响推力线横移的因素分析
典型的发动机喷管结构如图1所示,由图可见影响推力线横移的因素包括两部分:在发动机轴线和喷管扩张段轴线之间,各配合面间安装间隙的尺寸误差以及各连接环节的同轴度误差。本例中,影响推力线横移的因素包括:壳体尾端配合面轴线与壳体轴线的同轴度误差(因素1);壳体与喷管配合面之间的安装间隙(因素2);扩散段轴线与喷管配合面轴线同轴度误差(因素3)。喷管结构越复杂,在扩散段和发动机轴线之间的连接、装配环节越多,影响推力线横移的因素也就越多。

图1 发动机喷管结构示意图
一般在发动机设计中,尺寸误差只控制配合面实际尺寸的变化量在设计给定的极限尺寸之内,不控制形位公差;而同轴度只控制被测要素的形位公差,与实际尺寸无关。因此,对于这两类误差,属于按独立原则设计的零件要素,在建立推力线横移的尺寸链过程中,均可作为组成环计入。
1.2 推力线横移的数学模型
以图1所示的典型发动机喷管结构为例,在不考虑误差引起推力线偏斜的情况下,影响横移的尺寸链关系可用图2表示。
O点表示发动机轴线的投影,A点表示燃烧室后端配合面轴线的投影,B点表示喷管配合面轴线的投影,C点表示扩散段轴线的投影。用线段 OA、AB、BC分别代表因素1、因素2、因素3引起的横移大小,发动机推力线横移大小用线段OC表征。可以用向量的方法表示OC的大小以及相对于发动机轴线的方位。
由图2,将OA、AB、BC用3个向量表示,即:
向量 OA=(ρ1cosθ1,ρ1sinθ1)
向量 AB=(ρ2cosθ2,ρ2sinθ2)
向量 BC=(ρ3cosθ3,ρ3sinθ3)

图2 影响推力线横移的因素与发动机轴线间的关系
式中:ρ1、ρ3表示同轴度公差产生的横移的大小,ρ2为尺寸误差产生横移的大小,θ1、θ2、θ3分别表示不同误差产生的横移相对于基准的方位角。
向量OC=OA+AB+BC=

设OC(ρ,θ),C点在以 O点为极点的极坐标下,则有:
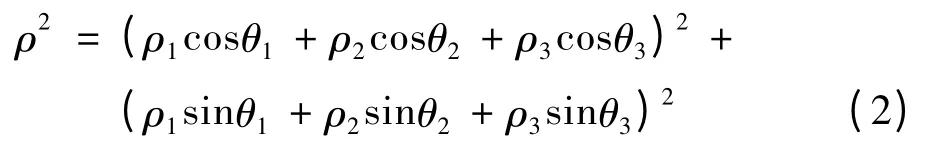
根据上式可确定ρ,取ρ≥0。
若 ρ1cosθ1+ ρ2cosθ2+ ρ3cosθ3= 0,ρ1sinθ1+ρ2sinθ2+ ρ3sinθ3> 0,则 θ = π/2,反之,ρ1sinθ1+ρ2sinθ2+ ρ3sinθ3< 0,则 θ =3π/2。
若 ρ1cosθ1+ ρ2cosθ2+ ρ3cosθ3≠ 0,则:

由式(2)、式(3)可计算向量 OC的 ρ、θ,得到推力线横移的大小、方位。同理,如果有更多因素影响推力线横移,可参照上述方法进行计算。
1.3 参数的取值及分布形式
得到了推力线横移表达式,只要知道 ρ1、ρ2、ρ3、θ1、θ2、θ3等参数值,即可计算出横移大小和方向角。
在本例中,ρ1、ρ3为同轴度误差,对于同轴度这种上、下偏差为对称分布的形位公差,无论是增环还是减环,对封闭环的影响都是相同的,在计算过程中,它的大小表示为0±T/2(其中T为同轴度公差值),概率分布为瑞利分布。ρ2为尺寸公差,由设计公差确定,取值范围为装配间隙的下偏差 /2~上偏差 /2,概率分布为正态分布。θ1、θ2、θ3为装配方位误差,概率分布为均匀分布,取值范围0~2π。
2 计算方法
蒙特卡洛(Monte Carlo)法[5]亦称为随机模拟(randomation)方法,有时也称作随机抽样(random sampling)技巧或统计试验(statistical testing)方法,是以概率统计理论为基础的一种方法。
它的基本思想是为了求解数学、物理、工程技术以及生产管理等方面的问题,首先建立概率模型或随机过程,使它的参数等于问题的解;然后通过对模型或过程的观察或抽样试验来计算所求参数的特征,最后给出所求解的近似值,而解的精确度可用估计标准误差来表示。
在应用蒙特卡洛方法进行公差分析的过程中,一般有如下的步骤[4]:
1)确定封闭环与组成环的尺寸、公差及其分布特征和传递系数,并确定分布函数;
2)根据模拟精度要求确定模拟次数N;
3)根据各组成环的分布规律进行随机抽样,从而得到各组成环尺寸的随机数列;
4)在得到各组成环的模拟值后,代入到尺寸链方程中,计算得到封闭环的数值;
5)重复3)、4)步骤N次,即可得到封闭环尺寸的N个子样。
文中采用MATLAB软件进行编程,计算推力线横移大小、方位角,通过程序实现蒙特卡洛模拟计算,随机数由MATLAB软件中相应的函数产生,分别由normrnd、raylrnd、unifrnd函数表征正态分布、瑞利分布、均匀分布。
3 算例
某发动机设计为:壳体尾部配合面与壳体轴线的同轴度为0.05mm;壳体尾端与喷管的安装间隙为0.043~0.293mm;扩散段轴线与喷管配合面轴线的同轴度为0.2mm,采用MATLAB编程计算,相关计算参数见表1。计算次数为200000次,统计结果见图3、图 4。

表1 参数设置

图3 推力线横移大小仿真统计结果

图4 推力线横移方位角仿真统计结果
由图可见,横移大小呈瑞利分布,方位角呈均匀分布。在置信水平0.9973时,该发动机推力线横移不大于0.189mm,小于极值法计算的0.2715mm。与极值法相比,蒙特卡洛法的计算结果更符合实际加工、装配情况;在设计要求确定时,通过计算可以方便的评估设计结果,也可以根据仿真结果进行公差分配,适当增大组成环公差,降低加工成本。
4 结论
通过对影响固体火箭发动机推力线横移的因素进行分析,建立了推力线横移的数学模型,给出了基于极坐标法的数学表达式,采用蒙特卡洛法对推力线横移进行了仿真计算。结果表明,采用该方法能够方便、迅速完成推力线横移的计算,可以在满足设计要求的前提下使零件的加工误差得到合理分配,为在发动机设计阶段优化结构设计参数、评估设计结果提供依据。
[1]刘文,张卫华,周珞晶,等.固体火箭发动机推力偏斜和横移对自旋火箭弹射程和横偏影响[J].弹箭与制导学报,1999,19(2):35 -38.
[2]张春富,唐文彦,李慧鹏,等.激光跟踪仪在固体火箭发动机推力线测量中的应用[J].固体火箭技术,2007,30(6):548-551.
[3]来平安,田维平,余贞勇,等.固体火箭发动机推力线横移和偏斜模拟计算[J].固体火箭技术,1999,22(1):35-38.
[4]王晶,石宏,黄笑飞,等.基于蒙特卡罗模拟法的航空发动机装配公差分析[J].沈阳航空工业学院学报,2010,27(4):8-11.
[5]徐钟济.蒙特卡罗方法[M].上海:上海科学技术出版社,1985.
