基于群智能方法的移动通信网络功率控制方法研究
2013-12-07刘晓曼
池 越,刘晓曼
(河北工业大学信息工程学院,天津 300401)
基于群智能方法的移动通信网络功率控制方法研究
池 越,刘晓曼
(河北工业大学信息工程学院,天津 300401)
功率控制技术作为移动通信网络优化的关键技术之一,其性能的好坏将直接影响移动通信网络的优化效果。通过对功率控制原理的研究,从联合功率控制与速率控制的角度出发提出了功率控制简化模型。而Grad-PSO算法是一种典型的群智能算法,已被广泛应用于工程优化问题之中。通过算法在函数优化过程中的仿真实验,验证了其在收敛速度、运算精度和运算量等方面具有优势。主要采用Grad-PSO算法对功率控制模型进行了优化仿真实验,通过仿真实验发现:Grad-PSO算法能找到最优解,很好地实现了对功率控制模型的优化。结果表明基于Grad-PSO算法功率控制优化方法切实可行,是一种有效的优化移动通信网络技术的方法。
移动通信;功率控制;群智能算法; Grad-PSO
目前,移动通信网络用户数量不断增加,业务范围不断增大,网络设备日益多样化。这就要求移动通信网在保证通信质量的同时,能为更多用户提高更为多样化的服务。因此,对于移动通信相关技术的要求也相应的越来越高[1-2]。功率控制技术作为移动通信网络的关键技术之一,可有效地克服由于“远近效应”带来的使用相邻或邻近信道的用户彼此间的临道干扰[3-5],从而大大提高移动通信网络的网络容量和通信质量。
针对移动通信网络的功率控制问题,国内外学者进行了大量的研究,多种优化算法已被应用到这一问题当中,如基于遗传算法、基于蚁群算法和基于粒子群(PSO)算法的功率控制方法等[6-8]。所有算法对解决移动通信网络的功率控制问题都起到了一定的推动作用,但由于这些算法存在着收敛速度较慢、运算精度较低和容易陷入局部最优等缺点,因此大大影响了功率控制的实时性和准确性。目前,基本PSO算法提出了许多改进算法。Grad-PSO(Grad-particle swarm optimization)算法是一种将梯度法引入PSO算法中构成的具有梯度搜索因子的改进PSO算法,该算法的优越性在大量工程优化实践中是已被证明的。它提供了一种求解复杂系统优化问题的有效方法,且不依赖于问题的具体领域,对所求解问题的种类具有很强的鲁棒性,在神经网络训练、目标函数优化、模糊系统控制等领域都得到了广泛应用[9-10]。这里将运用Grad-PSO算法对移动通信网络功率控制进行优化,以提高功率控制的实时性和准确性。
1 改进的PSO算法及原理
PSO算法是将优化问题中的每一个解称作一个“粒子”,所有粒子的适应度值(fitness)都由将被优化的目标函数决定。此外,每个粒子都有一个运动速度,粒子们会在解空间中追随当前最优粒子进行迭代搜索,直至找到最优解。粒子是通过在每一次迭代中跟踪2个“极值”来对自己进行位置更新。粒子本身找到的最优解称作个体极值pbest;整个种群当前找到的最优解称作全局极值gbest。粒子需要更新自己的速度和位置,如式(1)、式(2)所示:
vi=ωvi-1+c1×r1×[pbest-xi-1]+c2×r2×[gbest-xi-1],
(1)
xi=xi-1+vi。
(2)
式中:vi,vi-1分别表示当前粒子移动速度和上一次的粒子移动速度;xi,xi-1分别表示当前粒子位置和上一次粒子位置;ω表示惯性权重;pbest和gbest分别表示个体极值和全局极值;c1,c2表示学习因子,一般取c1=c2=2;r1,r2是取值范围在0到1之间的随机数[11]。
结合传统值优化方法在运算速度和精度上的优势,为了进一步提高PSO算法的收敛速度,将梯度法引入PSO算法中,构成具有梯度搜索因子的Grad-PSO算法。算法假设在域空间S中,优化函数f有全局最小值,在半径为r的圆A的圆心g点处为函数的全局最小值f(g),则圆A所包含的范围内为最优区域。在粒子远离全局最优值时,仍采用PSO算法原有的位置更新策略进行位置更新。而当粒子在邻近全局最优值时,则采用梯度法对其位置进行更新。这样可以有效减少PSO算法粒子随机更新位置所带来的时间负荷。因为当粒子一旦进入最优区域,就采用具有递减性的梯度法指导粒子更新到最佳位置,可加快算法的寻优速度。此外,梯度法的引入,虽然在一定程度上损失了PSO算法的随机性和灵活性,但它可以保证进入最优区域的粒子不会离开最优区域,大大提高了单寻优效率,从而进一步提高了算法的整体寻优效率[12-13]。Grad-PSO算法速度和位置的具体更新方法如式(3)—式(5)所示:
vi=ωvi-1+c1×r1×[pbest-xi-1]+c2×r2×[gbest-xi-1],
(3)
x=x+v,f(x)>f(g)+r,
(4)
x=T(x),f(x)≤f(g)+r。
(5)
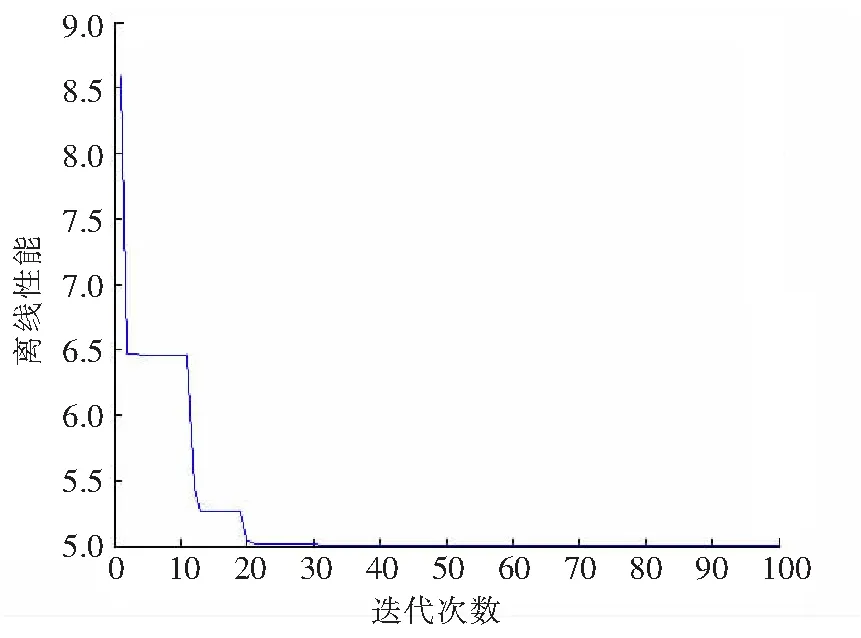
图1 Grad-PSO算法优化函数仿真结果Fig.1 Simulation result of function optimization by Grad-PSO algorithm
为了验证这种改进的Grad-PSO算法的优势,对下面的数学问题进行分析。目标函数为minf(x)=x2+2x+6;约束条件为-10≤x≤10。该问题为一带边界约束的一元函数的优化问题。已知全局最优解为f(x)=5.000 0。采用Matlab进行编程,仿真结果如图1所示。
仿真实验表明Grad-PSO算法由于存在梯度搜索因子,在优化函数时表现出了更富于规则化,呈现出很高的优化效率与很大的精确度,可以得出结论:Grad-PSO算法为一种更加有效的函数优化算法。
2 功率控制的数学模型
在以CDMA技术为基础构建的蜂窝移动通信系统中,用户终端在上下链路传输数据时采用相同的频谱,用户之间会存在干扰。以宽带CDMA蜂窝移动通信系统为例,存在着所谓“远近效应”,它与用户通信时的信道功率直接相关。因此,必须通过对用户终端的信号功率进行控制来克服“远近效应”的影响。另外,通过优化基站的发射功率,可以使每个用户终端都能接收到合理的基站辐射功率。
在移动通信系统中,系统容量的大小和频谱利用效率的高低,直接取决于每一个用户的信号功率和传输速率。针对移动通信网络功率控制这一问题,综合考虑功率控制与速率控制的影响建立了数学模型。设系统为一个有N个用户的多小区DS-CDMA蜂窝移动通信系统,扩频带宽W为N个用户共享,且每个用户对传输速率、时延和误码率的要求均不同[14-15]。为简化分析,限定了每个用户的最大发射功率Pmaxi和最小传输速率Rmini,并用目标比特能量噪声比Eb/N0来对应用户的误码率要求,用在一定范围内可变的传输速率来对应用户的时延要求。令hii表示用户i到其所属基站接收机的信道增益,hij表示用户j到用户i所属基站接收机的信道增益,Pi为第i用户的信号发射功率,目标Eb/N0为γi。令基站接收机处背景噪声为加性高斯白噪声,噪声的单边功率谱密度为η0,则Eb/N0即为基站接收到用户i信号:
(6)
式中,i=1,2,3,…,N。
为降低对其他小区用户的干扰,采用总发射功率最小化的准则进行优化。考虑到系统超负荷时,必须保证有服务质量要求的业务传输,提出优先级控制策略是:在严格保证高优先级业务的前提下,通过加大发射功率尽可能提高低优先级业务的传输质量。因此,采用系数Ai来表示各用户的优先级情况,该优化问题的目标函数以式(7)表示,约束条件为式(8)—式(10)。
min∑AiPi,
(7)
(8)
0≤Pi≤Pmaxi,
(9)
Ri≥Rmini。
(10)
3 改进PSO算法功率控制仿真实验
为了方便计算,对上述数学模型做了适当简化,从较为简单的N=2的情况入手,设N=2,i=1,2,P1=x1,P2=x2,R1=y。根据移动通信网络中的实际情况,设W=100 MHz,η0=2×10-8,h11=2,h12=3,h21=1.5,h22=2.5,γi=0.8,Pmax1=Pmax2=1 W,Rmini=50 Kb/s,权重系数A1=30,A2=100。采用Grad-PSO算法对功率控制进行优化仿真实验。其目标函数如式(11)所示,约束条件如式(12)—式(16)所示。
f(x1,x2)=min(30x1+100x2),
(11)

(12)

(13)
0≤x1≤1,
(14)
0≤x2≤1,
(15)
y≥50。
(16)
Grad-PSO算法具体处理流程如下。
Step1: 对算法各个参数进行设置,如种群包含粒子的个数,即种群的大小m=20,惯性权重系数ω=0.9和加速度常数c1=c2=2;
Step2: 对种群的粒子进行任意初始化(群体规模为N),计算确定所有粒子的适应度;
Step3: 评价Step2中计算得出的每个粒子的适应度;
Step4: 将每个粒子的适应度值fitness与历史最好位置pbest进行比较,如当前粒子适应度值更优,则将pbest更新为当前适应度值;
Step5: 对每个粒子,将其适应度值fitness与种群经过的历史最佳位置gbest进行比较,如果当前群体中最好的适应度值优于历史最佳位置gbest,则将其更新为gbest;
Step6: 根据算式对每个粒子的位置和速度进行更新;
Step7: 计算性能指标,看其是否达到优化结束条件,如达到条件,则返当前结果为最优解,算法结束;否则返回Step3,继续下一循环。
通过运用Grad-PSO算法对目标函数进行求解运算,可得最优解为x1=0.691 6,x2=0.486 0,此时目标函数为f=55.514 0,达到移动通信网络优化功率控制的要求。
图2、图3是Grad-PSO算法离线性能曲线在迭代次数为5,初始粒子数为10和20时的变化情况以及对比。

图2 迭代次数为5初始粒子数为10Fig.2 Number of iterations is 5 and the particle number is 10

图3 迭代次数为5初始粒子数为20Fig.3 Number of iterations is 5 and the particle number is 20
对比图2和图3不难看出,Grad-PSO算法在初始粒子数目不同,使得在同样迭代次数相同的情况下它们的收敛速度和收敛路径不同,但最终它们都能得到的最优解是相同的。
图4至图9是Grad-PSO离线性能曲线初始粒子数分别选用10和20时,迭代次数分别为20,40,100时的变化情况以及对比。

图4 迭代次数为20初始粒子数为10Fig.4 Number of iterations is 20 and the particle number is 10

图5 迭代次数为20初始粒子数为20Fig.5 Number of iterations is 20 and the particle number is 20

图6 迭代次数为40初始粒子数为10Fig.6 Number of iterations is 40 and the particle number is 10

图7 迭代次数为40初始粒子数为20Fig.7 Number of iterations is 40 and the particle number is 20

图8 迭代次数为100初始粒子数为10Fig.8 Number of iterations is 100 and the particle number is 10

图9 迭代次数为100初始粒子数为20Fig.9 Number of iterations is 100 and the particle number is 20
表1中是初始粒子数分别为10和20两种情况下,粒子最佳位置x1,x2和目标函数值f随迭代次数的变化情况。通过图3至图9以及表1中的数据不难看出,Grad-PSO算法随着迭代次数的增加,越来越接近最优值,不会由于随机性原因而远离最优解;而且初始粒子数不同,使得在同样迭代次数相同的情况下它们的收敛速度和收敛路径不同,但是它们都能很快地找到功率控制目标函数的最优解,实现功率控制函数优化。

表1 粒子最佳位置和目标函数值随迭代次数的变化情况
4 结 语
功率控制是移动通信网络中的一项关键技术,对功率控制进行优化具有重要意义。Grad-PSO算法具有收敛速度快、运算精度高等特点,采用该算法实现对移动通信网络功率控制的优化,大大提高了功率控制的实时性和准确性,基于Grad-PSO算法功率控制优化方法切实可行,是一种有效的优化移动通信网络技术的方法。
/
[1] 王晓霞, 耿海存, 陈艳红. 3G移动通信中功率控制技术分析[J].现代电子技术,2010 (9):81-83.
WANG Xiaoxia,GENG Haicun,CHEN Yanhong. Analysis of power control technology used in 3G communication[J]. Modern Electronics Technique, 2010(9):81-83.
[2 ] 李 庆,梁 云,胡捍英. WCDMA 系统中功率控制的研究[J ].通信技术,2008,41(2):120-122.
LI Qing,LIANG Yun,HU Hanying. Study on power control in WCDMA[J]. Communications Technology, 2008,41(2):120-122.
[3 ] 田素贞,屈芳升,刘传领. 一种自适应变步长的功率控制技术新算法[J ].青岛科技大学学报(自然科学版),2012,33(3):312-314.
TIAN Suzhen, QU Fangsheng, LIU Chuanling.A new algorithm of power control technique based on adaptive variable step size[J]. Journal of Qingdao University of Science and Technology(Natural Science Edition),2012,33(3):312-314.
[4 ] 解 梅,张自然. WCDMA 系统功率控制研究[J]. 电子科技大学学报,2003,32(4):354-357.
XIE Mei,ZHANG Ziran. Analysis of power control in WCDMA[J]. Journal of University of Electronic Science and Technology of China, 2003,32(4):354-357.
[5] 吴春艳. CDMA 移动通信快速功率控制中的几个影响因素[J]. 计算机仿真,2004,21(7):75-77.
WU Chunyan. Some factors effecting the fast power control of CDMA systems[J]. Computer Simulation, 2004,21(7):75-77.
[6] 文晓聪, 张会生, 许家栋. 一种基于遗传算法的功率控制方法[J].西北工业大学学报,2006,24(1):50-53.
WEN Xiaocong,ZHANG Huisheng,XU Jiadong. A new and better power control approach in cellular mobile communication system[J]. Journal of Northwestern Polytechnical University, 2006,24(1):50-53.
[7] 张曦煌,张 鹿. 基于蚁群的移动Ad hoc 功率控制算法的改进[J].计算机工程与设计,2007,28(19):4 664-4 667.
ZHANG Xihuang,ZHANG Lu. Improvement on Ad hoc power control algorithms in MANET based on ant[J]. Computer Engineering and Design, 2007,28(19):4 664-4 667.
[8] 王 宇,李少谦,李乐民. CDMA 蜂窝移动通信系统中的联合功率控制[J]. 电子学报,2000,28(11):114-118.
WANG Yu,LI Shaoqian,LI Lemin. Joint power control in CDMA cellular mobile communication systems[J]. Acta Electronica Sinica, 2000,28(11):114-118.
[9] 张学良,温淑花,李海楠,等. PSO 算法在多目标优化问题中的仿真应用[J]. 农业机械学报,2007,38(7):112-115.
ZHANG Xueliang, WEN Shuhua, LI Hainan,et al. Applications of particle swarm optimization in multi-objective problems[J].Transactions of the Chinese Society for Agricultural Machinery, 2007,38(7):112-115.
[10] 王荣海, 胥勋涛, 申 慧.基于粒子群优化算法的多目标搜索算法 [J]. 兵工自动化, 2013,32(1): 24-27.
WANG Ronghai,XU Xuntao,SHEN Hui. Multi-cbjective searching algorithm based on particle swarm optimization[J]. Ordnance Industry Automation, 2013,32(1): 24-27.
[11] 孙 磊,贾云献,王卫国,等. 基于粒子群优化核独立分量的特征降维算法及其应用研究[J].河北科技大学学报,2013,34(1):60-66.
SUN Lei,JIA Yunxian,WANG Weiguo,et al.A new algorithm of power control technique based on adaptive variable step size[J]. Journal of Hebei University of Science and Technology, 2013,34(1):60-66.
[12] 张立岩,张世民, 秦 敏. 基于改进粒子群算法排课问题研究[J].河北科技大学学报, 2011,32(3):265-268.
ZHANG Liyan,ZHANG Shimin,QIN Min. Research in improved particle swarm optimization for schedule arrangement[J]. Journal of Hebei University of Science and Technology, 2011,32(3):265-268.
[13] 朱 冰,齐名军. 混合粒子群优化算法[J]. 计算机工程与应用,2012,48(9):47-50.
ZHU Bing, QI Mingjun. Hybrid particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2012,48(9):47-50.
[14] KENNEDY J. Stereotyping: Improving particle swarm performance with cluster analysis [A] . Proceedings of the Congress on Evolutionary Computing [C].NJ: IEEE Service Center, 2000. 1 507-1 512.
[15] 原 萍,王光兴,张洋洋.求解通信优化问题的一种微粒群优化方法[J].东北大学学报(自然科学版),2004,25(10):934-937.
YUAN Ping, WANG Guangxing, ZHANG Yangyang. Particle swarm optimization approach of solving communication optimization problems[J]. Journal of Northeastern Universuity(Natural Science Edition), 2004,25(10):934-937.
Research of power control of mobile communication network based on swarm intelligence method
CHI Yue, LIU Xiaoman
(School of Information Engineering, Hebei University of Technology, Tianjin 300401, China)
As one of the key technologies of mobile communication network optimization, power control will directly affect the optimization result of the mobile communication network. Based on the study of power control principle, a simplified model is proposed from the viewpoint of power control and rate control. The Grad-PSO algorithm is a typical swarm intelligence algorithm, and it has been widely used in engineering optimization. Through function optimization simulation, the algorithm shows advantages of high convergence speed, accuracy and computational arithmetic. The algorithm is used to optimize the power control model. Simulation results show that there is an optimal solution and the optimization of power control model is well realized. The results show that the method is feasible and effective.
mobile communication; power control;swarm intelligence algorithm; Grad-PSO
1008-1542(2013)04-0334-06
10.7535/hbkd.2013yx04022
TP18
A
2013-03-12;
2013-06-18;责任编辑:陈书欣
河北省科学技术研究与发展项目(11213565)
池 越(1977-),男,河北唐山人,讲师,博士,主要从事通信技术和智能信息处理方面的研究。
E-mail: chiyueliuxin@126.com
