短波突发MPSK信号高效解调算法研究*

张婷，王彬

（解放军信息工程大学 信息工程学院，河南 郑州 450002）

短波通信作为现代无线通信的重要组成部分，在军事和民用方面具有不可取代的作用。现代短波通信系统常使用突发方式，传输的信号具有结构性强、持续时间短、受电离层信道影响大等特点，对接收端高效解调提出了特殊要求。

MPSK(MultiplePhase Shift Keying)是短波突发通信常用的调制方式，对其解调算法的研究也一直是研究的热点。参考文献[1-2]研究了先验信息缺失条件下的短波突发信号的盲解调算法。然而，在合作通信过程中，通信双方对先验信息是已知的，如果能够充分利用突发信号所包含的前导信息和训练数据，势必能够提高信息恢复能力和质量。参考文献[3]提出了一种数据辅助的突发信号解调算法，该算法没有考虑短波信道的特性，仅在加性高斯白噪声信道下有效。参考文献[4]比较详细地研究了第三代短波通信中BW2波形[5]的解调算法，充分考虑了信号的先验信息以及信道衰落影响，但是该算法具有载波参数和定时恢复精度低、均衡算法复杂度高等问题。

本文在已有研究的基础上，提出了一种新的MPSK突发信号的解调方案，以分数间隔均衡器和内置二阶锁相环的符号间隔判决反馈均衡器的三级均衡器结构为框架，结合联合的帧同步与高精度载波校正算法实现多径衰落信道条件下的MPSK信号高效解调。新的解调方案对短波突发MPSK信号的解调具有普遍适用性,系统性能较好。

1 信号模型

短波突发通信MPSK信号发送端模型如图1所示。

在发送端，信源信息经过信道编码以后，添加前导序列，根据一定的数据格式进行成帧，然后进行星座映射和成型滤波，最后将信号调制到相应载波频率上，经天线发射出去，通过短波信道到达接收端。

图1 短波突发MPSK信号发送模型

发送信号s(t)的数学模型可以表示为：

其中ck为信息数据序列，fc为载波频率，Ts为符号周期，g(t)为根升余弦成形滤波器。

发送信号经过短波信道后，设接收信号是r(t)，可以表示为：

短波电离层反射信道比较复杂，对窄带通信通常采用Watterson信道模型。CCIR提出的典型短波信道均为两径模型，不同条件下的信道参数如表1所示[6]。

表1 短波信道参数

2 高效解调算法研究

[4]以第三代短波高速数据BW2波形为研究对象，设计了如图2所示的解调结构。

图2 参考文献[4]解调方案

对接收信号首先进行下变频，然后利用接收数据中的前导序列进行载波频偏校正和帧同步，最后采用基于改进的Kalman滤波算法的判决反馈均衡器去除码间干扰，恢复出发送序列。该算法采用滑动相关FFT搜索谱峰实现载波校正与帧同步，存在精度低、运算量大的缺点；同时，没有位同步环节，无法处理实际通信过程中收发双方时钟源存在时钟频率偏差的问题；Kalman滤波算法的运算量大,实现复杂度高。

为了解决上述问题，本文提出了一种新的短波突发信号解调结构，如图3所示。

图3 短波突发MPSK信号解调框图

首先，利用接收信号中的前导序列进行高精度载波校正和帧同步，然后根据分数间隔均衡器对定时不敏感的特性，实现联合均衡和定时同步，最后用带锁相环的符号间隔判决反馈均衡器进一步纠正相位偏差并去除剩余码间干扰。

2.1 帧同步与高精度载波校正

2.1.1 帧同步

接收机要从接收信号中恢复出所传输的信息,首先进行帧同步，判定信息序列的起始。实现同步有很多方法，其中滑动相关法是最简单、最实用的方法。

假设接收信号为r(t)：

其中，f1和φ1分别表示接收端载波频率和相位，c(t)为发送信息码元序列，对接收信号进行采样记为r(k)：

假设本地载波为 f0，则本地序列表示为c(m)e-j(2πf0m+φ0)，用本地序列与接收序列得到：

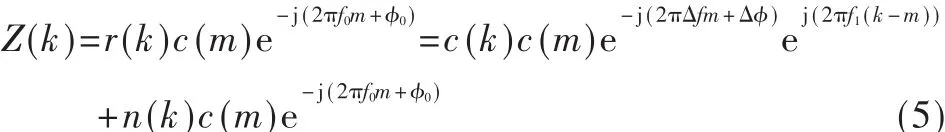
△f=f0-f1为收发双方存在的频差，△φ=φ0-φ1为固定相差。当本地序列与接收序列同步,即 m=k，c(m)c(k)=1时，对信号Z(k)作FFT变换出现明显谱峰，捕获到信号，实现了帧同步。同时，谱峰处也是粗估得到的载波频率位置。

2.1.2 载波校正

参考文献[4]利用已知的前导和训练序列进行滑动相关，然后用补零的方法进行高分辨率FFT，通过谱峰搜索得到频偏，该方法运算量大，估计精度低。

参考文献[7]提出了一种快速高精度载波估计算法。该算法首先通过补零方法计算2倍前导序列长度的相关FFT，以达到提高频谱分辨率的目的。假设信号前导序列长度为L，2×L点的傅里叶变换表达式为：

对频谱进行谱线搜索，得到载波频率粗估计值为：

该估计值是分辨率的整数倍，而实际频偏ε是一个实数，所以ε与ε^之间存在一个小数的差值△ε。由于紧邻峰值的左右两条谱线也包含载波频偏的信息，利用这两条谱线进行插值运算，可以得到差值的估计值△ε^，插值计算式如下：

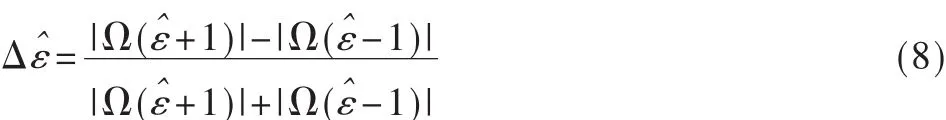
该算法通过谱线插值对载波频偏进行了无偏的精确估计，估计性能明显优于参考文献[4]。本文采用参考文献[7]的方案进行载波校正。

2.2 分数间隔均衡实现定时同步

为了克服收发双方时钟频率存在的定时偏差，除了完成帧同步得到数据起始码元时刻，还需要对其后的接收数据进行码元定时同步。考虑到传统的基于环路锁相方式的定时恢复算法跟踪时间比较长，不适用于短时突发信号；另外，通常收发双方时钟频率偏差比较小，可以利用分数间隔均衡器对定时不敏感的特性，实现联合均衡与定时同步的功能[8]。在参考文献[8]的基础上，利用有数据辅助的分数间隔均衡结构，用训练序列调整均衡器抽头系数，克服定时时钟频率偏差积累对均衡器抽头系数的影响。

考虑到突发信号的训练序列往往比较短，需要均衡器较快达到收敛状态。采用递归最小二乘算法(RLS)进行均衡器抽头更新。图4是其基于RLS算法的T/4分数间隔均衡器的结构图。

图4 基于RLS算法的T/4分数间隔均衡器

RLS算法采用指数加权的误差平方和作为代价函数，即：

其中，加权因子 0＜λ＜1称为遗忘因子。设置 en(i)表示期望响应与 i时刻抽头输入为 x(i),x(i-1),…,x(i-M+1)的横向滤波器输出y(i)之差，M为滤波器长度，即：

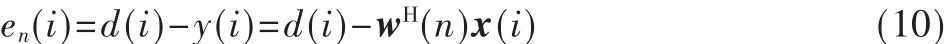
预测误差进行修正时的比例系数，C(n)为 R(n)的逆矩阵，递推公式为C(n)=R-1(n)=[C(n-1)-g(n)xH(n)C(n-1)]，RLS算法的系数迭代更新公式为:

用n-1时刻的最佳加权和wH(n-1)x(n)对n时刻数据的期望响应 d(n)进行预测，得到预测误差 e(n)，实现 RLS算法的递推。

2.3 内置二阶锁相环的判决反馈均衡

为了提高解调性能，降低误码率，需进一步减小上述处理结果中存在的剩余载波相偏和剩余码间干扰。本文采用内置二阶锁相环的判决反馈均衡器实现上述功能。如图5所示。

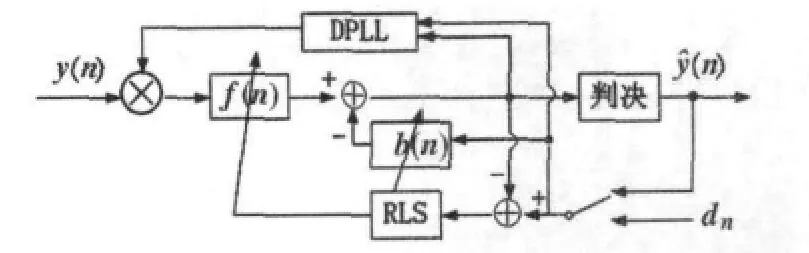
图5 内置二阶锁相环的DFE结构

判决反馈均衡器由前馈滤波器、反馈滤波器和判决器三部分组成，前馈滤波器和反馈滤波器是符号间隔的FIR滤波器，其抽头系数更新算法仍然采用RLS算法。反馈滤波器的功能是利用先前的判决值来消除由前面检测出的符号对当前待检测符号上产生的码间干扰。判决器用于判断均衡器输出信号与哪个发送信号的距离最近，从而给出判决值。对训练序列采用数据辅助的方法确定均衡器抽头系数。

由于较大的剩余相位偏差会严重影响均衡器的性能,本文引入了跟踪性能较好的内置二阶锁相环(DPLL)进行相位误差纠正。二阶锁相环载波相位更新方程为:

其中，K1、K2为二阶锁相环的增益因子，eφ(n)为 n 时刻的相位误差。通过相位跟踪进行实时相位补偿，减少了由于相位偏差引起的判决误差。

3 仿真结果

以第三代短波通信协议中的高速数据BW2波形为例，对本文算法进行仿真和性能分析。BW2波形的调制方式为8 PSK，码元速率为2 400 B,载波频率为1 800 Hz，前导序列和训练序列总长为304个符号，数据部分长为2 880个符号，采样率为9 600 Hz。

3.1 载波估计性能分析

为了测试本文采用的联合的帧同步与高精度载波校正算法的估计性能，将其与参考文献[4]算法进行比较。设置信噪比 Eb/N0从0 dB～10 dB，载波频偏为 30 Hz，经过线性时不变衰落信道ch2=[0.407,0.815,0.407]，计算估计的频偏与实际频偏的差的绝对值相对于符号速率的归一化频差，进行100次蒙特卡罗统计平均，结果如图6所示。

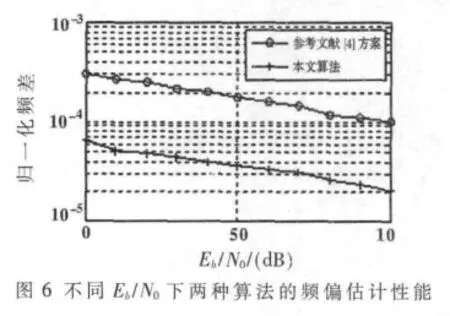
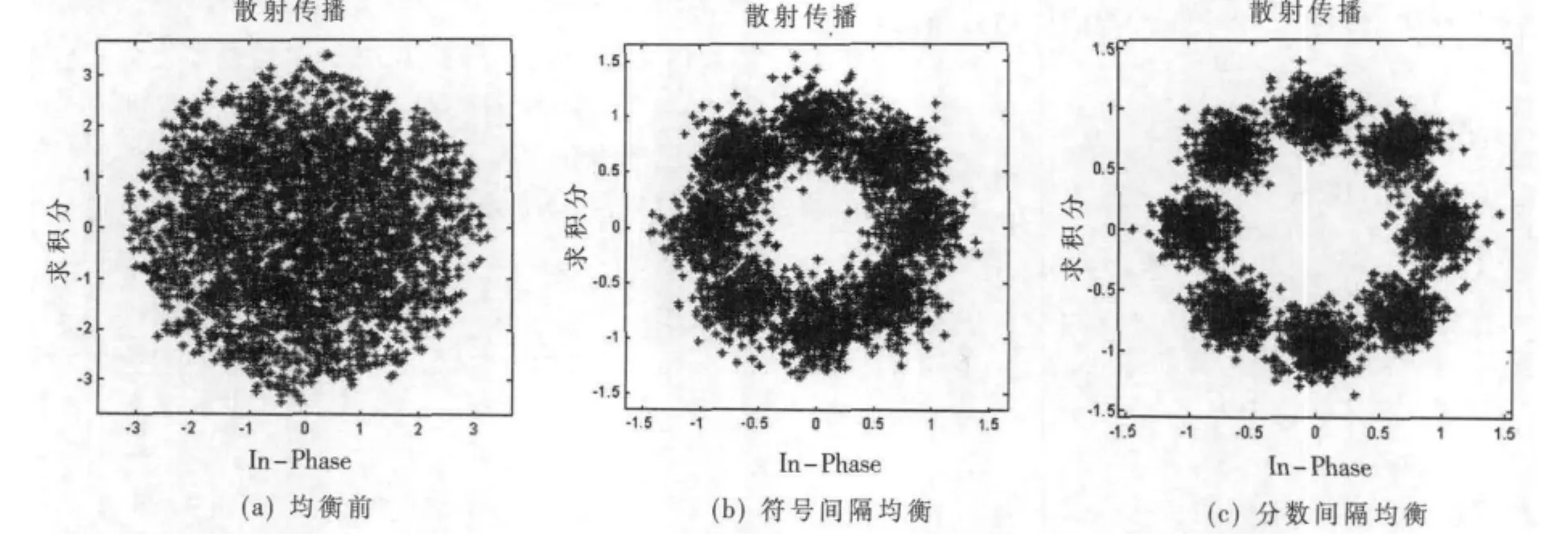
图7 符号间隔均衡与分数间隔均衡的星座图

结果表明，本文采用算法精度比参考文献[4]算法精度高一个数量级，同时本文算法进行2×L(L=240)点 FFT运算，而参考文献[4]进行4 096点 FFT运算，运算量小得多。

3.2 分数间隔均衡实现定时同步性能分析

为了说明分数间隔均衡实现均衡与定时的性能，在未完成定时的条件下，分别将信号通过分数间隔均衡器与符号间隔均衡器进行收敛。在信噪比Eb/N0为18 dB时，经过线性时不变衰落信道ch2=[0.407,0.815,0.407]，两种均衡器结构下BW2信号的星座图，如图7所示。

由图7发现,分数间隔均衡器不受采样相位影响，能够较好地实现定时同步，且均方误差小，星座图清晰、紧凑。

3.3 系统误比特性能分析

仿真测试本文提出的解调结构在不同短波突发信道下的性能。采用本文解调结构，分别经过线性时不变衰落信道 ch2=[0.407,0.815,0.407]，CCIR好信道和中度信道，进行100次蒙特卡罗统计平均，得到的误比特率结果如图8所示。

图8 不同信道下的误码率

由结果可知，本文设计解调方案对时不变或慢时变的多径衰落性能较好，在Eb/N0为20 dB时误码率达到10-4以下。对于时变较快和频率选择性衰落较大的CCIR中度信道，系统性能恶化。而短波突发信道可近似为时不变或慢时变的多径衰落信道。

本文采用三线FFT快速高精度载波估计算法，以基于RLS算法的分数间隔均衡和内置二阶锁相环的符号间隔判决反馈均衡的三级均衡器结构完成信号定时和收敛，实现解调。本文算法运算量小，复杂度低，能很好地改善信号质量减小码间干扰，适用于短波突发信号的解调。但是对于时变较快和频率选择性衰落较大的恶劣短波信道，则需要进一步研究。

参考文献

[1]贺军,郭伟.一种新的消除V&V算法载波相位模糊的方法[J].电子与信息学报，2006，28(05):836-839.

[2]徐翔辉,段田东,韩俊峰,等.一种短波突发信号的联合定时同步结构[J].计算机应用与软件,2010，27(06):190-191,235.

[3]HONG D K,KIM D J,LEE Y J.A simple interpolation technique for the DFT for joint system parameters estimation in burst MPSK transmissions[J].IEEE Trans Commun,2003,51(7)：1051-1056.

[4]林娟.短波数据传输关键技术研究[D].西安电子科技大学，2010.

[5]MIL-STD-188-141B Appendix C.Third generation HF link automation[R].United States of America:Department of Defense,1999:264-439.

[6]ITU.Use of high frequency ionospheric channel simulators[R].Dubrovnik:International Radio Consultative Committee,1986:57-58.

[7]龚超,张邦宁,郭道省.基于FFT的快速高精度载波参数联合估计算法[J].电子学报，2010,38(4):766-770.

[8]许华.短时突发信号的盲处理技术研究[D].郑州:解放军信息工程大学,2005.

[9]张宏立,于宏毅,吴绍民.短波突发通信中自适应均衡算法研究[J].信息工程大学学报,2007,8(2):175-178.