DC/DC变换器的PWA模型及预测控制*
2013-12-07刘晓东
方 炜,王 青,刘晓东
(安徽工业大学 电气信息学院,安徽 马鞍山 243000)
随着新一代功率集成电子器件的不断出现,开关功率变换器越来越广泛地应用于人们的日常生活。目前大多数的研究工作是通过提出新的拓扑结构和先进的控制策略来提高功率变换器的各种性能。但是相当一部分控制算法依然基于较早提出的状态空间平均法建立的系统模型。由于这种小信号建模的方法忽略了功率变换器中开关器件的离散动作,因而存在很大的局限性[1-2]。
事实上,由于开关器件的离散动作和连续动态特性的相互作用,功率变换器是一个典型的混杂动态系统。因此,如何利用混杂系统理论对DC/DC功率变换器进行研究,已引起国内外专家学者的广泛关注。参考文献[3]利用周期性切换模型分析了DC/DC功率变换器的混杂动态特征,并研究了系统的能控性、能观性和能达性;参考文献[4]研究了Boost功率变换器的混杂控制问题,通过设计混杂控制律调节变换器的输出电压;参考文献[5]基于滑模观测器建立了DC-DC变换器的混杂系统状态模型,基于混杂系统模型设计了预测控制器;参考文献[6]运用混杂系统相关理论,研究二阶DC-DC变换器的统一混杂系统模型,基于Lyapunov直接法分析系统稳定性,进而提出了一种新型的类滑模控制策略。
模型预测控制 MPC(Model Predictive Control)利用内部模型预测系统的状态或输出,同时应用有限时域的滚动计算和反馈校正对系统性能指标进行优化计算,以确定在预测控制时域内的最优控制序列,具有控制效果好、鲁棒性强等优点[7]。
本文利用混杂系统理论对DC/DC功率变换器进行建模分析。首先,利用变换器的υ步离散法,得到输入控制变量与状态变量之间的直接映射关系,研究和分析开关动态与连续动态(状态变量)之间的相互作用,进而建立能够准确反应开关变换器混杂动态特征的分段仿射模型(PWA)。在此模型的基础之上,结合非线性预测控制,通过对预测模型的推导以及反馈校正环节的合理设计得到最优占空比序列,设计预测控制器。最后以Buck变换器为例,验证模型建立的正确性以及控制器设计的有效性。
1 DC/DC变换器的PWA模型
1.1 Buck变换器的数学模型
DC/DC功率变换器是一种典型的切换系统。其工作过程是在多个线性系统之间进行周期性的切换。以Buck变换器为例建立数学模型,拓扑结构如图1所示。

假设变换器工作在电流连续状态,那么它有两个工作模态。状态变量 x(t)=[il(t)vc(t)]T,il(t)是电感电流,vc(t)是电容电压,d(k)是第k个周期的占空比信号。Buck变换器的状态空间方程为:

其中:

由以上分析可以看出:在电流连续模态下的变换器,由于开关管Q1存在两种不同的工作模态,从而使得Buck变换器呈现混杂系统的动态特征。整个工作过程是在两个子系统之间进行切换,系统的结构参数和模式不再固定,不能用统一的简单运动模型来描述,因而其控制的实现也变得复杂。
1.2 变换器的步离散模型
在建立混杂动态模型时,最关键的就是如何描述开关动态与连续动态之间的相互作用。为此,将一个开关周期 TS细分为 υ(υ≥2)个子区间[8]。 每个子区间的周期τS=TS/υ。
为了确定子区间的类型,引入υ个二元变量并定义如下:σn=1⇔d(k)≥n/υ,n=0,1,…,υ-1。 它代表开关 Q1在nτS时刻的状态。在每个子区间开关有两个状态 (开通与关断)。子区间可以划分为三类:
(1)在整个子区间内Q1处于关断状态;
(2)在整个子区间内Q1处于导通状态;
(3)子区间处于Q1由导通转向关断的过渡状态中。
因此,在第n个采样周期中子区间按以下公式进行状态更新:
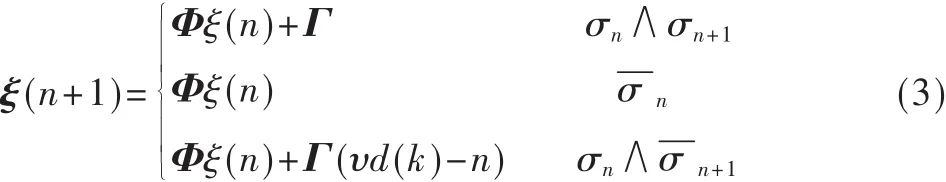
1.3 变换器的PWA模型
通过以上分析,以υ=3为例得到Buck变换器的PWA模型:

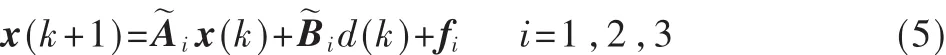
由此υ步离散模型可以得到精确的时间离散模型,即PWA切换仿射模型,如式(5)所示;建立了占空比控制矢量和状态变量之间的准确映射关系式,体现了开关动作与系统状态的直接关系。
2 模型预测控制
2.1 预测模型
假设所有的状态可测,预测步长为Hp,控制步长为Hu,且Hu≤Hp。为求解预测控制问题,由迭代模型式(5)来进行预测,可以得到:


因此,可以得到输出y的预测值:

2.2 误差反馈校正
由于实际应用中存在模型失配、环境干扰等不确定因素,当k时刻将控制d(k)作用于控制对象,利用预测模型所计算出来的输出预测值y^(k+1)有可能与实际的输出值y(k+1)不相符,这时就需要构成预测误差:

并用此误差对输出预测进行反馈校正:
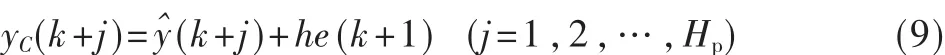
将其写成矢量形式:

式中,H=[h1h2… hHp]T是误差加权矩阵,仅在预测输出与实际输出存在偏差时才起作用。这一误差校正的引入,也使得系统成为一个闭环负反馈,提高了系统的性能。
2.3 求解最优控制问题
一般来说,控制的目的是在外界扰动和环境干扰等条件下,让输出电压以很小的超调和调节时间跟踪期望的输出电压值。同时,在控制过程中,往往不希望控制作用的增量△d的变化过于剧烈,这一因素可在优化性能指标中加入软约束予以考虑。因此,k时刻的优化性能指标可取为:
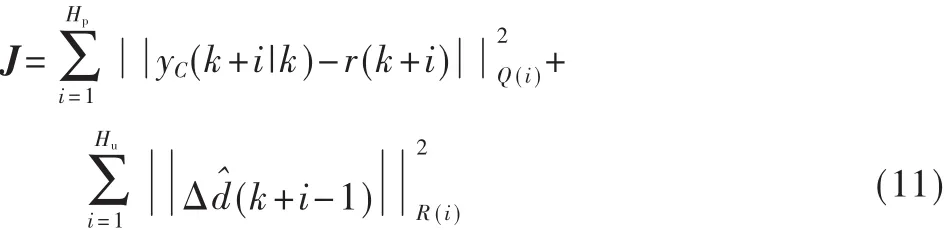
其中,Qi是加权系数,Ri分别表示对跟踪误差及控制作用变化的抑制。
式(11)可以改写为:
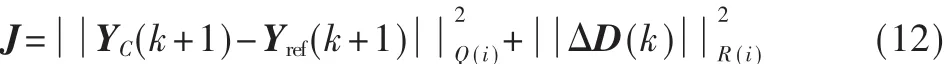
由△D(k)opt=min J求未来输入增量的最优集合:

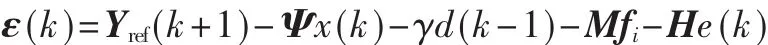
由以上分析可知,相应的滚动策略中仅利用这个解第一步,假设装置的输入个数为l,因此:
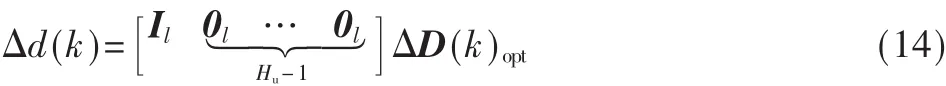
式中,Il是 l×l的单位矩阵。
由以上分析可知,预测控制的控制策略是在实施△d(k)之后,采集k+1时刻的输出数据进行新一轮的预测、校正、优化。由此可以看出,优化过程不是一次离线进行的,而是反复在线进行的,其优化目标也是随着时间推移的,即在每一时刻都提出一个立足于该时刻的局部优化目标,而不是采用不变的全局优化目标。
3 Simulink仿真
仿真环境为Microsoft Windows XP Professional系统,Matlab7.1软件仿真平台。
负载瞬态性能是衡量DC/DC变换器的一个重要性能指标。以Buck电路为例进行仿真。假设在电流连续模态下主电路输入电压Vg=5 V,参考电压2.5 V,开关频率fS=400 kHz, 电容电感参数分别为:C=200μF,L=1μH,子区间为 3,预测步长和控制步长分别为:Hu=Hp=2。将仿真结果与峰值电流模式相比较如下。
(1)负跃变情况(10 A→5 A)
图2(a)是预测控制和峰值控制下输出电压变化的仿真波形图。在0.001 s时刻负载电流由10 A到5 A时,由于电感电流不能突变,输出电压即刻增加。由图2(b)可知,每个开关周期占空比信号的数值是离散的、成周期性变化的,在预测控制的作用下,每个周期对电感电流和输出电压进行一次采样并结合前一时刻的占空比计算出当前时刻要施加到系统上的最优控制占空比信号,从而实现了实时调节的作用。这样,输出电压即可在很短的时间内调节恢复稳态跟随参考电压,调节时间 35μs,超调量 95.3 mV,而峰值电流模式的调节时间为 188μs。
(2)正跃变情况(5 A→10 A)
为进一步对两种算法进行对比,对负载电流正跃变进行仿真验证。
由图3知,预测控制的调节时间35μs,欠调量为96 mV,而峰值电流模式的调节时间为150μs。欠调量为110 mV。
以上分析可知,分段仿射模型实现了控制变量(占空比)与状态矢量(输出电压)的直接控制变化离散关系,预测控制算法通过最优占空比离散的、周期性变化的计算,实现了实时在线优化控制。两者的结合对电路的输出电压进行控制,使在负载跳变时,对输出的电压影响很小,可以很快地调节电压,恢复稳态。因此,DC/DC变换器在预测控制策略下,具有良好的动态响应特性和稳态特性。

本文从混杂系统理论角度出发,考虑开关变换器的开关切换特性,对DC/DC变换器进行了建模和仿真分析。首先分析了变换器的混杂特性,为了得到状态变量和控制矢量之间的直接映射关系,利用υ步离散法,得到了相对精确的模型,即PWA模型。随后提出了系统的优化性能指标并基于PWA模型设计了预测控制器。仿真实验表明,在纯阻性负载扰动的情况下,预测控制的效果相对峰值电流模式有一定的优势,它能快速地调节电压恢复稳态值。系统具有良好的动态性能和稳态性能,进而验证了模型的正确性和控制算法的有效性。
[1]陆益民,张波,尹丽云.DC/DC变换器的切换仿射系统模型及控制[J].中国电机工程学报,2008,28(15):16-22.
[2]KAVITHA A,UMA G.Experimental verification of hopf bifurcation in DC-DC luo converter[J].IEEE Transactions on Power Electronics,2008,23(6):2878-2883.
[3]胡宗波,张波,邓卫华,等.PWM DC-DC变换器混杂动态系统的能控性和能观性[J].电工技术学报,2005,20(2):76-82.
[4]SREEKUMAR C,AGARWAL V.A hybrid control algorithm for voltage regulation in DC-DC boost converter[J].IEEE Transactions on Industrial Electronics,2008,55(6):2530-2538.

[5]FRIEDRICH M O,JASON N,STEVE P,et al.MPC of switching in a boost converter using a hybrid state model with a sliding mode observer[J].IEEE Transactions on Industrial Electronics,2009,56(9):3453-3466.
[6]马皓,祁峰,张霓.基于混杂系统的DC-DC变换器建模与控制[J].中国电机工程学报,2007,27(36):92-96.
[7]郑雪生,李春文,戎袁杰.DC/AC变换器的混杂系统建模及预测控制[J].电工技术学报,2009,24(7):87-92.
[8]BECCUTI A G,PAPAFOTIOU G,MORARI M.Optimal control of the boost estimation for inferential DC/DC converter[C].Proceedings of the 44th IEEE Conference on Decision and Control,and the European Control Conference,2005:4457-4462.
