SVR算法在太阳黑子活动预测上的应用

涂光辉 蒋 华

(桂林电子科技大学计算机科学与工程学院，广西 桂林 541004)

1 引言

机器学习是人工智能的核心研究领域之一， 其最初的研究动机是为了让计算机系统具有人的学习能力以便实现人工智能，因为众所周知，没有学习能力的系统很难被认为是具有智能的。目前被广泛采用的机器学习的定义是：“机器学习是研究计算机算法，并通过经验提高其自动性“[1]。”基于数据的机器学习是现代智能技术中的重要方面，研究从观测数据（样本）出发寻找规律，利用这些规律对未来数据或无法观测的数据进行预测[2]“（张学工）。包括模式识别、神经网络等在内，现有机器学习方法共同的重要理论基础之一是统计学。

统计学习理论（Statistical Learning Theory或SLT）是一种专门研究小样本情况下机器学习规律的理论。V.Vapnik等人从六、七十年代开始致力于此方面研究[3]。随着其理论的不断发展和成熟，在这一理论基础上发展了一种新的通用学习方法——支持向量机（Support Vector Machine或SVM）。SVM为解决基于数据的非线性建模问题提供了一个新思路，是一种具有严密理论基础的计算机学习的新方法，它已经成为计算机学习、模式识别、计算智能、预测预报等领域的热点技术，受到国内外的广泛关注。

机器学习的目的是根据给定的训练样本求对某系统输入输出之间依赖关系的估计，使它能够对未知输出作出尽可能准确的预测[2]。本文通过使用支持向量机算法，对上证指数进行预测。所得的预测结果对现实生活中的股票投资有一定的参考作用。

2 算法描述

2.1 支持向量机

支持向量机建立在结构风险最小化原则(SRM)[4]基础之上，是统计学习理论中最年轻的内容，也是最实用的内容。其核心内容是在1992到1995年间提出的[5,6,7,8]，目前仍处在不断发展阶段。具有很强的学习能力和泛化性能，能够较好地解决小样本、高维数，非线性、局部极小等问题，可以有效地进行分类、回归、密度估计等[9]。另外支持向量机在处理非线性问题时 首先将非线性问题转化为高维空间中的线性问题然后用一个核函数来代替高维空间中的内积运算从而巧妙地解决了复杂计算问题并且有效地克服了维数灾难及局部极小问题。由于有这些优点，支持向量机已成为机器学习领域的研究热点。目前，支持向量机已经已经广泛用于解决分类和回归问题[10,11]。

2.2 回归问题的数学描述

回归问题[12]的数学提法是：已知训练集T ={(x1, y1),( x2, y2), …,( xl, yl)}∈(X *Y)，其中 xi∈X=Rn是输入指标向量，或称输入，或称模式，yi∈Y=R是输出指标，或称输出，i = 1,2,… ,l。假定训练集是按X*Y上的某个概率分布P( x, y)选取的独立同分布的样本点，又设给定损失函数L( x, y, f)。试寻求一个函数f( x)，使得期望风险R( f ) =∫L( x, y, f) d P( x, y )达到极小。此处概率分布P( x, y)是未知的，已知的仅仅是训练集T。

2.3 支持向量回归与核函数

设给定的训练样本[13]为：首先用一个非线性映射φ把数据映射到一个高维特征空间，然后在高维特征空间中进行线性回归设回归函数为：f( x) =＜ w, φ(x) ＞+b 。优化问题是最小化

式(1)中第一项使函数更为平坦，从而提高泛化能力，第二项则为减小误差，常数C对两者做出折中。ε为一正常数，f( xi)与yi的差别小于ε时不计入误差，大于ε时误差计为|f( xi) -yi|-ε。

这是一个二次优化问题， 其对偶问题为：

解这个二次优化，可以得到a的值，ω的表达式为：

于是回归函数 f( x)的表达式为：

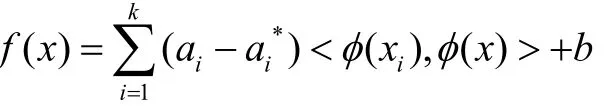
可以看到 在上面的优化中需要计算高维特征空间中的内积运算，如果找一个核函数k( x, y)代替高维空间中的内积，就可以避免复杂的高维计算问题。已经证明 ＜φ( x),φ(y)＞，对称函数k( x, y)只要满足 Mercer 条件，即可满足要求，这样就避免了明确知道φ(x)，从而巧妙地解决了在高维空间中的运算。按照Kuhn-Tucker 定理，可得b的计算式如下：

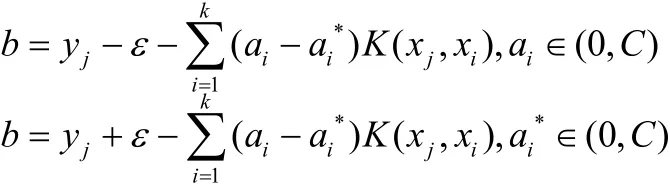
可以通过任意一个满足条件的样本计算出b的值。

核函数的选择是支持向量机理论研究的一个核心问题。在实际的应用中，最常用的核函数[14]有以下4种：

式中σ为核参数，它隐式地定义了从原始空间到高维特征空间中的非线性映射。

（4）Sigmoid函数

在这四种核函数中，应用最广泛的是RBF核，无论是低维、高维、小样本、大样本等情况，RBF核函数均适用，具有较宽的收敛域，是较为理想的分类依据函数[15]。本论文使用的是RBF核函数。

2.4 LS_SVM的数学原理

最小二乘支持向量机是支持向量机的一种改进，它是将传统支持向量机中的不等式约束改为等式约束，且将误差平方和( Sum Squares Error)损失函数作为训练集的经验损失，这样就把解二次规划问题转化为求解线性方程组问题，提高求解问题的速度和收敛精度。设样本为n维向量, 某区域的l个样本及其表示为：首先用一非线性映射ψ(·)把样本从源空间 Rn映射到特征空间φ ( xi)，在这个高维特征空间中构造最优决策函数∶

这样非线性估计函数转化为高维特征空间的线性估计函数。利用结构风险最小化原则，寻找ω，b就是最小化：

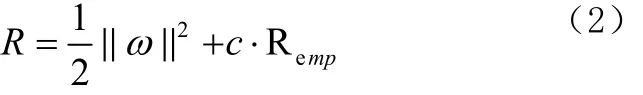
其中，‖ ω ‖2控制模型的复杂度，c是正规化参数，控制对超出误差样本的惩罚程度。Remp为误差控制函数，也即ε不敏感损失函数。常用的损失函数有线性ε损失函数，二次ε损失函数，Huber损失函数。选取了不同的损失函数，可构造不同形式的支持向量机。最小二乘支持向量机在优化目标失函数为误差ξi的二次项。故优化问题为

式中，iξ为松弛因子。用拉格朗日法求解这个优化问题∶

其中：αi( i =1,…, l )是拉格朗日乘子。

其中：αi=c ·ξi, ω · φ( xi) +b + ξi- yi=0。

定义核函数 K( xi, yi) = φ( xi) ·φ( xj)是满足条件的对称函数。优化问题可转化为求解线性方程[18]：

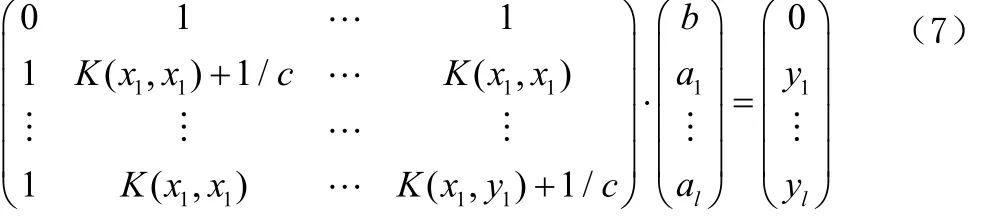
最后用最小二乘法求出a与b，最小二乘支持向量机也由此得名，并且得到非线性预模型：

3 数据集描述

本论文使用的数据集是太阳黑子。太阳黑子（sunspot）是在太阳的光球层上发生的一种太阳活动，是太阳活动中最基本、最明显的。黑子看上去像一些深暗色的斑点，很少单独活动，常是成群出现。黑子的活动周期为11.2年，活跃时会对地球的磁场产生影响，主要是使地球南北极和赤道的大气环流作经向流动，从而造成恶劣天气，使气候转冷。严重时会对各类电子产品和电器造成损害。

当太阳上有大群黑子出现的时候，地球上的指南针会乱抖动，不能正确地指示方向；平时很善于识别方向的信鸽会迷路；无线电通讯也会受到严重阻碍，甚至会突然中断一段时间，这些反常现象将会对飞机、轮船和人造卫星的安全航行、还有电视传真等方面造成很大的威胁。黑子还会引起地球上气候的变化，从而对农作物的生长和人的身体造成不可忽视的影响。

黑子的活动是有规律的，对人类活动有重要影响。我们很有必要对它进行必要的研究，掌握一些基本的规律以指导人类的活动。本文对1780～1979年的黑子活动进行了实验。分别将1879～1958年和1780～1958年间的太阳黑子的数据作为训练集，相应的年份作为 X，而太阳黑子数作为Y;1959-1979期间的数据作为测试集，其中的年份作为Xt，太阳黑子数作为tY。

4 LS_SVM工具箱介绍自编程序说明

最小二乘支持向量机（LSSVM）是标准的支持向量机的改进形式。LSSVM与正规化网络[16]和高斯函数紧密相关，但它更加重视对偶问题的求解。它将经典的模式识别算法，如核Fisher判别分析和扩展的无监督学习和神经网络联系到一起[17]。LSSVM是一类基于核的学习方法，它最基本的目标是解决分类问题和回归问题。

LS_SVM工具箱用于函数回归主要用到 3个函数，trainlssvm函数用来训练建立模型，simlssvm函数用于预估模型，plotlssvm函数是LS2SVMlab工具箱的专用绘图函数。高版本的LS2SVMlab工具箱还有贝叶斯框架下的最小二乘支持向量机，固定大小的最小二乘支持向量机等。

本论文使用SVR算法，对太阳黑子的活动进行回归预测。具体代码如下：

%读取数据

t=textread('E∶数据集.txt');

%提取训练集

X=t(1∶80,1);%（X=t(1∶180,1)）

Y=t(1∶80,2);% (X=t(1∶180),1)

%提取测试集

Xt=t(81∶100,1);

Yt=t(81∶100,2);

%初始化参数

gam = 10;

sig2 = 0.5;

fold = 5;

type = 'function estimation';

costfun = 'rcrossvalidate';

costfun_args = {X,Y,fold};

optfun = 'gridsearch';

%生成最优参数

[gam, sig2] = tunelssvm({X,Y,type,gam,sig2}, [],optfun, {}, costfun, costfun_args);

%交叉验证

performance = rcrossvalidate({X,Y,type,gam,sig2},costfun_args);

%算法训练,建立模型

[alpha,b] = robustlssvm({X,Y,type,gam,sig2});

%进行模型的预测

Yt = simlssvm({X,Y,type,gam,sig2},{alpha,b},Xt);

%输出曲线

plotlssvm({X,Y,type,gam,sig2},{alpha,b});

5 实验结果及分析

经过调试程序，用1879-1958年的太阳黑子数训练后得到的测试结果如图（1）示。用1780～1958年的太阳黑子数训练后得到的测试结果如图（2）所示。其中实线表示预测的太阳黑子数，点表示实际的太阳黑子数。

从图（1）中容易观察到黑字数的真实值与预测值的在顶点时有一定的误差，但总体的拟合程度还是比较高。这说明用SVR算法来预估太阳黑子数能得到较好的预估效果。从图（2）容易发现黑字数的真实值与预测值的在顶点时有比较大的误差。从这两个测试结果的比较中，我们可以得出这样的结果：实验所用的训练黑子数的时间越靠前，所得的测试结果越准确。

图1

图2

6 结论

最小二乘支持向量机是用等式约束代替传统支持向量机中的不等式约束，求解过程从解QP问题编程一组等式方程，提高求解问题的速度和收敛精度。针对最小二乘支持向量机在回归预测方面的应用，使用SVR算法建立了太阳黑子数的预测模型。预测结果表明最小二乘支持向量机建立的非线性模型是可行有效的，具有很好的泛化能力，计算速度快。

[1] T. M. Mitchell. Machine Learning[M].New York: McGraw-Hill,1997.

[2] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.

[3] Vapnik V N. Estimation of Dependencies Based on Empirical Data[M]. Berlin: Springer‧Verlag, 1982.

[4] C．J．C Burges．A tutorial on support vector lIlachines for pattern recognition[J].Data Mining and Knowledge Discovery.1998,2(2):121-167.

[5] Vapnik V, Levin E, Le Cun Y. Measuring the VC‧dimension of a learning machine[J].Neural Computation.1994(6):851-876.

[6] Burges C J C. A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery,1998,2(2):121-167.

[7] Burges C J C. A tutorial on support vector machines for patternrecognition[J].1998(02):121-167

[8] Boser B,Guyon I,Vapnik V. A training algorithm for optimal margin classifiers[J]. 1992,5(20):61-65.

[9] Olvi L. Mangasarian, David R. Musicant.Successive overrelaxation for support vector machines[J].IEEE Transactions on Neural Networks.1999,5(10):1032-1037.

[10] Brassil J T, Low S H, Maxemchuk N F. Copyright Protection for the Electronic Distribution of Text Documents [J]. Proc. IEEE.1999,7(87):1181-1196.

[11] Lu H, Shi X, Shi Y Q, Kot A C, Chen L. Watermark embedding in DC components of DCT for binary images[C].in proc. IEEE Int.Workshop on Multimedia Signal Processing, US Virgin Islands. 2002:300-303.

[12] 杜树新,吴铁军.用于回归估计的支持向量机方法[J].系统仿真学报,2003,15(11):1580-1633.

[13] 孙德山,吴今培,肖健华.SVR在混沌时间序列预测中的应用[J].系统仿真报,2004,3(16):519-521.

[14] 苏高利,邓芳萍.关于支持向量回归机的模型选择[J].科技通报,2006,3(2):154-158..

[15] 李盼池,许少华.支持向量在模式识别中的核函数特性分析[J].计算机工程与设计,2005,26(2):302-304.

[16] Evgeniou T., Pontil M.,Poggio T. Regularization networks and support vector machines[J]. Advances in Computational Mathematics, 2000,13(1):1-50.

[17] Suykens J.A.K., Vandewalle J.Recurrent least squares support vector machines,IEEE Transactions on Circuits and Systems-I,2000,47(7),1109-1114.

[18] 阎威武,邵惠鹤.支持向量机和最小二乘支持向量机的比较及应用研究[J].控制与决策,2003,18(3):358-360.