E0互补问题的变形凝聚同伦算法
2013-12-03王秀玉姜兴武
王秀玉, 姜兴武, 李 琳
(1. 长春工业大学 基础科学学院, 长春 130012; 2. 吉林工商学院 基础部, 长春 130062)
考虑非线性互补问题: 求x≥0, 满足f(x)≥0, 且有xTf(x)=0, 其中f(x)=(f1(x),f2(x),…,fn(x))T是向量值的光滑函数. 当f为线性函数时, 互补问题称为线性互补问题. 当f为E0-映射时, 互补问题称为E0互补问题. 求解互补问题等价于求解下列非线性非光滑方程组:
(1)
上述互补问题广泛应用于经济、 工程生产及各种均衡模型中, 目前, 已有许多求解互补问题的方法, 如信赖域法[1]、 迭代法[2]、 投影法[3]、 例外族法[4]和同伦方法[5-9]等. 其中同伦方法由于具有大范围收敛性, 已成为求解非线性数学问题的重要工具之一. 文献[5-6]系统地研究了利用同伦方法求解互补问题; 文献[7]利用文献[5]的同伦方程讨论了半定线性互补问题的可解性; 文献[8]推广了文献[7]的结论, 给出了一类非单调互补问题解的存在性; 文献[9]建立了与文献[5-8]不同的同伦方程, 但缺少互补问题解存在的条件.
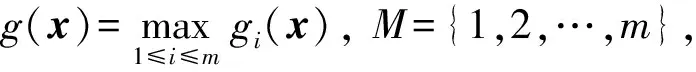
文献[10]研究了凝聚函数的性质, 给出g(x,μ)光滑逼近极大函数g(x). 本文利用凝聚函数的变形形式构造同伦方程, 对E0互补问题进行求解.
设x≥0(x>0)表示向量x的每个分量为非负(正)数;f′表示向量值函数f: Rn→Rn的Jacobi矩阵;h表示数量值函数h: Rn→R的梯度.
1 变形凝聚函数

1)g(x)≤g(x,μ)≤g(x)+μlnm;
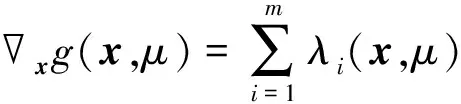
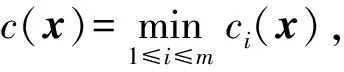
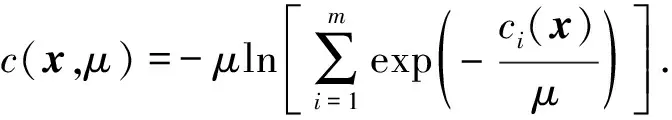

1)c(x)-μlnm≤c(x,μ)≤c(x);


本文令
φ: R2→R,φ(a,b)=-μln(e-a/μ+(1-μ)ce-b/μ),
c>0为常数,φ(a,b)称为变形凝聚函数. 显然有
φ(a,b)=-μln(e-a/μ+eln(1-μ)ce-b/μ)=-μln(e-a/μ+e-(b-μln(1-μ)c)/μ).
又由引理2可知
min(a,b-μln(1-μ)c)-μln2≤φ(a,b)≤min(a,b-μln(1-μ)c),
因而有
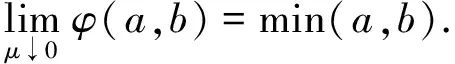
利用凝聚同伦方法求解非线性互补问题, 做如下假设:
(H1)fi(x)(i∈M)是Cl(l≥2)函数;

定义1[11]如果对任意的x,y∈Rn, 且x-y≥0, 必存在指标i, 使得xi>yi, 且有fi(x)≥fi(y), 则映射f称为E0-映射,E0-映射也称为半单调映射.
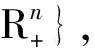
2 互补问题的变形凝聚同伦算法
H(x,x(0),μ)=Φ(x)-μx(0)=0,
(2)
其中
对于给定的x(0), 式(2)也记为
(3)

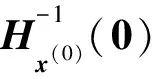
证明: 将x(0)视为变量, 将以x(0),x,μ为自变量的同伦方程记为Hx(0)(x,μ), 其Jacobi矩阵记为
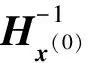
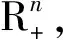

证明: 若Γx(0)是一条无界曲线, 则存在点列{(x(k),μk)∈Γx(0)}, 使得‖(x(k),μk)‖→∞, 由同伦方程(2)可得
(4)
解式(4)得
由式(5)得
(6)
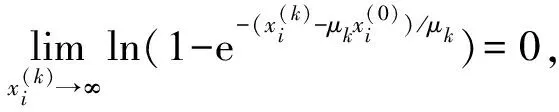
(7)
与条件1矛盾, 因此,Γx(0)是一条光滑的有界曲线.

证明: 由定理1和定理2易知Γx(0)为有界曲线. 由一维流形分类定理知,Γx(0)微分同胚于单位圆周或单位区间(0,1](证明与文献[9]的定理2.1类似). 注意到
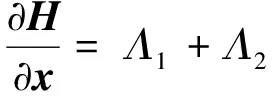
是非奇异的, 得Γx(0)不能微分同胚于单位圆周, 而只能微分同胚于单位区间. 记(x(*),μ*)为Γx(0)的极限点, 则只可能发生以下4种情形:
1)μ*∈[0,1], ‖(x(*)‖→∞;
2)μ*=1, ‖x(*)‖<∞;
3) ‖x(*)‖<∞,μ*∈(0,1), 且x(*)∈∂Θμ*;
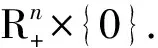

下面利用预估-校正算法对同伦方程(2)产生的路径进行跟踪, 从而得到非线性互补问题的解, 算法步骤与文献[12]相同.
命题1若Γx(0)为光滑曲线, 则在初始点x(0)处的正方向η(0)满足
证明: 由
得
(8)
其中
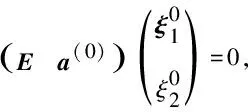
从而有
例1
经简单计算易知f为E0-映射且显然条件1成立. 计算结果列于表1.

表1 例1的计算结果
例2


表2 例2的计算结果
由表1和表2可见, 本文算法的计算速度和精度均优于文献[12].
[1] ZHU De-tong, CAI Li. Affine Scaling Interior Trust-Region Method for Solving Generalized Complementarity Problems with Linear inequality Constraints [J]. Chinese Annals of Mathematics, 2010, 31A(1): 13-34. (朱德通, 蔡力. 线性不等式约束的广义非线性互补问题的仿射内点信赖域方法 [J]. 数学年刊, 2010, 31A(1): 13-34.)
[2] Buhmiler S, Krejic N. A New Smoothing Quasi-Newton Method for Nonlinear Complementarity Problems [J]. Journal of Computational and Applied Mathematics, 2008, 211(2): 141-155.
[3] QU Biao, WANG Chang-yu, ZHANG Shu-xia. A Method for Solving Nonlinear Complementarity Problem and Its Convergence Properties [J]. Mathematica Numerical Sinica, 2006, 28(3): 247-258. (屈彪, 王长钰, 张树霞. 一种求解非线性互补问题的方法及其收敛性 [J]. 计算数学, 2006, 28(3): 247-258.)
[4] ZHAO Yun-bin, Isac G. Quasi-P*,P(τ,α,β)-Maps, Exceptional Family of Element and Complementarity Problems [J]. Journal Optimization Theory and Applications, 2000, 105(1): 213-231.
[5] Kojima M, Megiddo N, Mizuno M. A General Framework of Continuation Methods for Complementarity Problems [J]. Math of Oper Res, 1993, 18(4): 945-963.
[6] Kojima M, Megiddo N, Noma T. Homotopy Continuation Methods for Nonlinear Complementarity Problems [J]. Mathematics of Operations Research, 1991, 16(4): 754-774.
[7] YU Qian, HUANG Chong-chao, WANG Xian-jia. A Combined Homotopy Interior Point Method for the Linear Complementarity Problem [J]. Applied Mathematics and Computation, 2006, 179(2): 696-701.
[8] XU Qing, DANG Chang-yin. A New Homotopy Method for Solving Non-linear Complementarity Problems [J]. Optimization, 2008, 57(5): 681-689.
[9] DING Jun-di, YIN Hong-you. A New Homotopy Method for Nonlinear Comolementarity Problems [J]. Numericla Mathematics, A Journal of Chinese Universities: English Series, 2007, 16(2): 155-163.
[10] SONG Dai-cai, LIN Zheng-hua, LIU Guo-xin. Some Properties of the Aggregate Tunction [J]. Acta Scientiarum Naturalium Universitatis Jilinensis, 2000(2): 1-4. (宋岱才, 林正华, 刘国新. 凝聚函数的若干性质 [J]. 吉林大学自然科学学报, 2000(2): 1-4.)
[11] ZHAO Yun-bin, LI Duan. On a New Homotopy Continuation Trajectory for Nonlinear Complementarity Problems [J]. Mathematics of Operations Research, 2001, 26(1): 119-146.
[12] WANG Xiu-yu, JIANG Xing-wu, LIU Qing-huai. The Combined Homotopy Method for Nonlinear Complementarity Problems [J]. Acta Mathemxticae Applicatae Scinica, 2012, 29(2): 430-440. (王秀玉, 姜兴武, 刘庆怀. 非线性互补问题的组合同伦算法 [J]. 应用数学学报, 2012, 29(2): 430-440.)
