两类无约束优化的充分下降共轭梯度法

孙中波, 段复建, 高海音, 于海鸥

(1. 东北师范大学人文学院 数学系, 长春 130117; 2. 桂林电子科技大学 数学与计算科学学院, 广西 桂林 541004; 3. 长春大学 理学院, 长春 130022)

0 引 言

考虑无约束优化问题

(1)

其中:f: Rn→R1是连续可微函数; Rn为Euclidean空间. 对无约束优化问题(1), 一般采用线搜索方法进行近似求解, 即

xk+1=xk+αkdk,

(2)

其中:αk为线搜索步长; {xk+1}为迭代产生的迭代序列;dk为线搜索方向. 针对问题(1), 文献[1-7]分别给出了不同的共轭梯度公式, 进而得到不同的共轭梯度法, 即

时贞军等[8]提出一种混合共轭梯度法, 该方法通过引入参数μ, 得到一个新的共轭梯度公式:

(3)

其中μ∈[0,1]. 当μ=0时, 混合算法转化为PRP共轭梯度法; 当μ=1时, 混合算法转化为LS共轭梯度法. 根据算法产生的不同βk, 搜索方向的下降性也不同. 文献[8]中搜索方向的下降性取决于参数c的选取, 当c=1时, 该算法产生的搜索方向是充分下降的, 但当c=10-10时, 参数c很小, 每次迭代都不能产生充分下降方向,会严重影响算法的计算效率. 孙中波等[9]提出了另外一种混合共轭梯度法. 与文献[8]类似, 共轭梯度公式如下:

(4)

其中λ∈[0,1]. 当λ=0时, 混合算法转化为FR共轭梯度法; 当λ=1时, 混合算法转化为CD共轭梯度法. 由βk1产生的搜索方向也不能保证每次迭代都为充分下降方向. 如当δ/λ=0.999 99或者δ/λ充分接近1时, 算法的计算效率就会受到影响. 张利等[10]提出了两种混合共轭梯度算法, 即

及

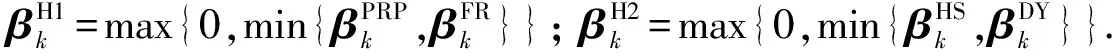
dk=-θkgk+βkdk-1,

(5)

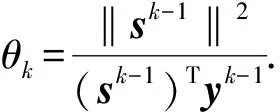
第一类搜索方向dk计算公式如下:

(6)

第二类搜索方向dk计算公式如下:

(7)

对于第一类搜索方向, 当λ=0时, 混合算法可以转化为FR共轭梯度法; 当λ=1时, 混合算法可以转化为CD共轭梯度法. 并且两个搜索方向dk均具有充分下降性. 在适当的条件下, 证明了算法是全局收敛的, 数值实验表明算法可行、 有效.

1 算 法

由式(2)可见, 迭代过程的产生离不开步长搜索, 即步长αk的求解. 搜索步长的产生有很多种, 如单调线搜索准则和非单调线搜索准则等, 包括有单调的Armijo,Wolfe,Goldstien准则和非单调的Armijo,Wolfe,Goldstien准则. 文献[13]提出了一个修正的Armijo准则:

本文结合文献[13], 采用推广到非单调的Armijo准则求解步长αk:

(8)

其中, 0≤m(k+1)≤min{m(k)+1,M},M为充分大的正整数.

算法1

初始化: 假设x0∈Rn为任意初始点, 0<λ<1,σ∈(0,1/2),m(0)=0,k∶=0. 步骤如下.

1) 终止条件判定并计算dk: 如果‖gk‖≤ε, 则算法停止; 否则分别采用式(6),(7)计算dk, 转2);

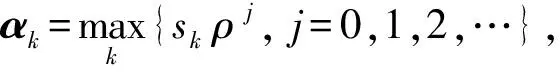
(9)

3) 计算xk+1: 令xk+1=xk+αkdk, 转4);

4)k=k+1, 返回1).

当步骤2)中的M=0时, 非单调线搜索算法即转化为单调线搜索算法. 算法1实际上是两类求解无约束优化问题的充分下降算法, 区别在于步骤1)中搜索方向dk的求解.

2 算法适定性

假设1水平集Λ={x∈Rn:f(x)≤f(x0)}有下界, 其中x0为初始点, 且Λ为有界闭凸集.

假设2目标函数f(x)的梯度f(x)是Lipschitz连续函数, 即存在常数满足

‖f(y)-∀y,z∈Rn.

由算法1知, 迭代序列{xk}始终保持在水平集Λ. 还可以得到如下结论: 存在一个正常数κ>0, 使得‖g(x)‖≤κ, ∀x∈Λ.

定理1假设1成立, 搜索方向dk由式(6)计算得到, 则(gk)Tdk=-‖gk‖2<0.

证明: 由算法1知, 有如下两种情况:

1) 若k=0, 则dk=-gk, 有(gk)Tdk=-(gk)Tgk=-‖gk‖2<0;

2) 若k>0, 则dk=-gk+βk1dk-1-νkgk, 其中βk1由式(4)确定, 有

注1当搜索方向为式(6)时, 算法1是适定的.

定理2假设1成立, 搜索方向dk由式(7)计算得到, 则(gk)Tdk=-‖gk‖2<0.

证明: 由算法1知, 有如下两种情况:

1) 同定理1中1);

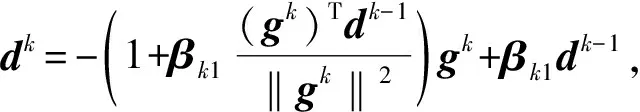
注2当搜索方向为式(7)时, 算法1是适定的. 由定理1和定理2可知, 算法1的充分下降性不需要线搜索保证, 搜索方向自身具有下降的性质.

3 全局收敛性分析

证明: 由算法1的步骤2)知,

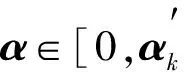
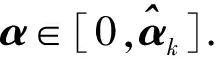
引理2如果存在一个正常数>0, 使得

‖gk‖≥, ∀k,

(10)

∀k.

(11)

证明: 由式(6)及假设1和假设2, 有

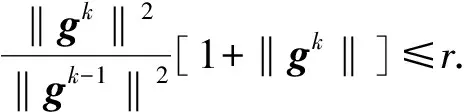
定理3假设1和假设2成立, {xk}由算法1生成, 每次迭代过程中, {dk}为式(6)产生的充分下降方向. 若αk由非单调Armijo线搜索, 则

(12)

‖gk‖≥, ∀k

(13)

成立. 下面分两种情况讨论：

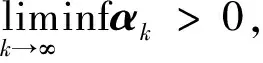
由算法1的步骤2)知, 当k∈Π充分大时,ρ-1αk不满足步骤2), 即

(14)

利用中值定理及其引理4知, 存在hk∈(0,1), 使得

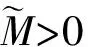
即

定理4假设1和假设2成立, {xk}由算法1生成, 每次迭代过程中, {dk}为式(7)产生的充分下降方向. 若αk由非单调Armijo线搜索, 则

(16)

证明: 由算法1及假设2和引理2, 有

其中

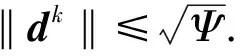
4 数值实验

本文采用Rosenbrock,Freudenstein Roth,Trigonometrix函数为测试函数[16]. 在Matlab7.1环境下编写程序代码: CPU为奔腾(R) 2.19 GHz, 1 Gb内存.

1) Rosenbrock函数:

2) Freudenstein Roth函数:

f(x)=[-13+x1+((5-x2)x2-2)x2]2+[-29+x1+((x2+1)x2-14)x2]2;

3) Trigonometrix函数:

表1 算法1数值结果

表2 文献[9]数值结果

表3 FR共轭梯度法数值结果

表4 CD共轭梯度法数值结果

表5 算法1为单调线搜索的数值结果

在表1中, 采用非单调线搜索产生搜索步长αk, 并且选取M=9. 由表1可见, 本文提出的算法可行、 有效. 在表2中, 文献[9]的算法在CPU时间和迭代步数上均超过了本文提出的算法1, 表明本文提出的充分下降方向确实优于文献[9]中的算法. 当λ=0时, 混合算法可以转化为FR共轭梯度法; 当λ=1时, 混合算法可以转化为CD共轭梯度法. 因此, 表3和表4分别是测试FR和CD共轭梯度法, 比较可见, 经典共轭梯度法的CPU所用时间和迭代步数均超过本文算法, 尤其当测试函数的维数较高时. 本文算法无论是从CPU时间, 还是迭代步数均比其他几个算法少, 显示了算法1的优越性. 在表5中, 选取M=0, 即算法1采用单调线搜索的情况, 数值结果表明, 非单调线搜索产生的步长比单调搜索步长更合理.

[1] Fletcher R, Reeves C M. Function Minimization by Conjugate Gradients [J]. The Computer Journal, 1964, 7(2): 149-154.

[2] Poliak B T. The Conjugate Gradient Method in Extreme Problems [J]. USSR Comput Math and Math Phys, 1969, 9(14): 94-112.

[3] Fletcher R. Practical Methods of Optimization [M]. New York: Wiley, 1987.

[4] Polak M R, Ribiere G. Note Sur la Convergence de Méthodes de Directions Conjuguées [J]. Revue Francaise d’Informatique et de Recherche Opérationelly, 1969, 16: 35-43.

[5] Liu Y, Storey C. Efficient Generalized Conjugate Gradient Algorithms, Part 1: Theory [J]. J of Optim Theorem and Appl, 1991, 69(1): 129-137.

[6] Dai Y H, Yuan Y. An Efficient Hybrid Conjugate Gradient Method for Unconstrained Optimization [J]. Ann of Oper Res, 2001, 103(1/4): 33-47.

[7] DAI Yu-hong, HAN Ji-ye, LIU Guang-hui, et al. Convergence Properties of Nonlinear Conjugate Gradient Methods [J]. SIAM J of Optim, 1999, 21: 348-358.

[8] SHI Zhen-jun, GUO Jin-hua. A New Family of Conjugate Gradient Methods [J]. J of Comput and Appl Math, 2009, 224(1): 444-457.

[9] SUN Zhong-bo, DUAN Fu-jian. A Class of Nonmonotone Conjugate Gradient Methods for Unconstrained Optimization [J]. Journal of Henan Normal University: Natural Science, 2010, 38(1): 12-15. (孙中波, 段复建. 一类无约束优化的非单调共轭梯度法 [J]. 河南师范大学学报: 自然科学版, 2010, 38(1): 12-15.)

[10] ZHANG Li, ZHOU Wei-jun. Two Descent Hybrid Conjugate Gradient Methods for Optimization [J]. J of Comput and Appl Math, 2008, 216(1): 251-264.

[11] Birgin E G, Martínez J M. A Spectral Conjugate Gradient Method for Unconstrained Optimization [J]. Appl Math & Optim, 2001, 43(2): 117-128.

[12] Raydan M. The Barzilain and Borwein Gradient Method for the Large Scale Unconstrained Minimization Problem [J]. SIAM J on Optim, 1997, 7(1): 26-33.

[13] ZHANG Li, ZHOU Wei-jun, LI Dong-hui. A Descent Modified Polak-Ribiere-Polyak Conjugate Gradient Method and Its Global Convergence [J]. IMA J of Numer Anal, 2006, 26(4): 629-640.

[14] ZHANG Li, ZHOU Wei-jun, LI Dong-hui. Global Convergence of a Modified Fletcher-Reeves Conjugate Gradient Method with Armijo-Type Line Search [J]. Numer Math, 2006, 104(4): 561-572.

[15] DUAN Fu-jian, SUN Zhong-bo. A Modified Liu-Storey Conjugate Gradient Method and Its Global Convergence for Unconstrained Optimization [C]//Proceeding of Chinese Control and Decision Conference. Shenyang: North East University Press, 2010: 1585-1588.

[16] More J J, Garbow B S, Hillstrom K E. Testing Unconstrained Optimization Software [J]. J ACM Trans on Math Software, 1981, 7(1): 17-41.