具有梯形结构大系统目标规划模型的求解算法

张 杰, 刘 妮, 徐玲敏

(东北电力大学 理学院, 吉林 吉林 132012)

由于大系统目标规划模型规模庞大、 结构复杂, 很难直接求解, 所以需要根据其特殊结构研究相应的求解算法, 目前已取得了一些成果. Shastri等[1]将所研究的问题先转化为两阶段随机规划问题, 再将对大型随机非线性规划问题的求解转化为对不确定变量重复加权, 并对目标函数和约束条件进行线性近似, 从而简化模型. Saadouli[2]利用聚合法解决大型随机动态规划问题, 先将系统分解为几个阶段, 然后利用仿真和人工智能思想相结合, 从而得出高精度的有效解. Regis[3]提出了求解大系统优化问题的随机径向基函数算法, 利用多重径向基函数近似模型中的目标函数和不等式约束, 得到替代模型, 并在每次迭代时运用这些模型为函数估计确定合适的点, 这种算法只需要相对较小的计算量即可得到较好的解. Anderson等[4]以生物系统为原型, 提出了两种求解生物大系统问题的算法----分解法和降阶法, 基本思路是对于不含不确定性参数的模型, 采用降阶法； 对于含有不确定性参数的情况, 采用分解法, 在保证原模型动态特性不变的前提下, 将模型分解成较小的子系统, 并对子系统进行仿真求解, 进而得到大系统的解. 文献[5]根据原方块角形结构大系统多目标规划问题的特征, 将其进行分解, 通过研究大系统模型与各个子系统模型最优解之间的关系, 给出了此类大系统问题最优解的判别条件. 文献[6]针对原方块角形结构大系统目标规划问题, 研究了分解子问题与大系统问题有效解之间的关系, 并讨论了大系统问题有效解的存在性. 文献[7-8]对具有梯形结构大系统多目标规划问题进行了初步研究, 通过对模型进行适当的分解, 探讨了大系统问题最优解与分解后子问题最优解的关系, 旨在将大系统问题的求解转化为求解子问题, 为研究这类大系统目标规划模型的有效求解算法奠定了基础. 本文在文献[7-8]的基础上, 先在纵向分解子问题对应的约束不等式组有解的条件下, 证明子问题(Pi)的最优解构成大系统问题(P)的最优解； 再针对一般情况, 提出求解梯形结构大系统目标规划模型的“顺次解耦算法”, 并结合实例说明了算法的迭代过程及其有效性.

1 大系统与纵向分解子系统约束不等式组解之间的关系

1.1 模型描述

其中各部分的含义与文献[8]相同.

大系统模型(P)所对应的约束不等式组为

(1)

纵向分解子问题(Pi)对应的约束不等式组为

(2)

1.2 大系统与纵向分解子系统约束不等式组解之间的关系

一般的多目标规划模型为

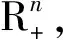
记模型(P′)的最优集为A(P′).

定理1若不等式组

(3)

有解, 设其解集为U(G), 则U(G)=A(P′).

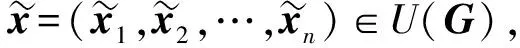
(4)

(5)

(6)

综上所述, 有U(G)=A(P′).

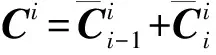
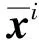
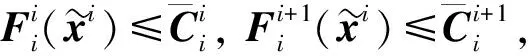
由定理1和定理2可得:

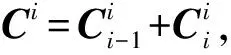
2 具有梯形结构大系统目标规划模型的顺次解耦算法及数值算例

2.1 顺次解耦算法的基本思想

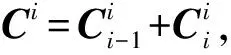
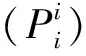
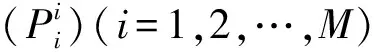
2.2 算法步骤

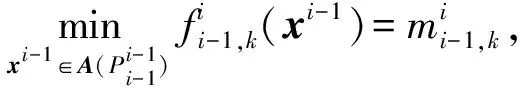
转4).

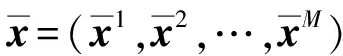
2.3 顺次解耦算法的数值算例

利用顺次解耦算法求解大系统目标规划模型(P)： 求x=(xij:i=1,2,3;j=1,2,3,4), 使得

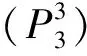
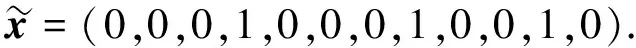
该解与直接对模型(P)求解得到的结果一致.

综上所述, 本文提出了求解具有梯形结构大系统目标规划模型的“顺次解耦算法”. 利用该算法, 每次迭代只需要对规模较小的子问题进行求解, 即可得到大系统问题的最优解.

[1] Shastri Y, Diwekar U. An Efficient Algorithm for Large Scale Stochastic Nonlinear Programming Problems [J]. Computers & Chemical Engineering, 2006, 30(5)： 864-877.

[2] Saadouli N. Computationally Efficient Solution Algorithm for a Large Scale Stochastic Dynamic Program [J]. Procedia Computer Science, 2010, 1(1)： 1397-1405.

[3] Regis R G. Stochastic Radial Basis Function Algorithms for Large-Scale Optimization Involving Expensive Black-Box Objective and Constraint Functions [J]. Computers & Operations Research, 2011, 38(5)： 837-853.

[4] Anderson J, CHANG Yo-cheng, Papachristodoulou A. Model Decomposition and Reduction Tools for Large-Scale Networks in Systems Biology [J]. Automatica, 2011, 47(6)： 1165-1174.

[5] ZHANG Jie, FENG Ying-jun. The Criteria of Optimal Solution on a Kind of Large Scale Goal Programming [J]. Journal of Mathematical Study, 2000, 33(2)： 163-168. (张杰, 冯英浚. 一类大系统目标规划问题分解算法中最优解之间的关系 [J]. 数学研究, 2000, 33(2)： 163-168.)

[6] ZHANG Jie, FENG Ying-jun. Existence of Effective Solution on Large Scale Multiobjective Programming with General Diagonal Structure [J]. Journal of Harbin Institute of Technology, 2001, 33(5)： 617-619. (张杰, 冯英浚. 一般原方块角形结构的大系统多目标规划有效解的存在性 [J]. 哈尔滨工业大学学报, 2001, 33(5)： 617-619.)

[7] ZHANG Jie, WEI Cai-xia. Relations of Solutions among Subproblems on Large Scale Multiobjective Programming with Trapezoidal Structure [J]. Journal of Jilin University： Science Edition, 2010, 48(2)： 237-240. (张杰, 魏彩霞. 梯形结构大系统多目标规划子问题解的关系 [J]. 吉林大学学报： 理学版, 2010, 48(2)： 237-240.)

[8] ZHANG Jie, XU Ling-min, HU Ding. Bidirectional Decomposition of Large Scale Multiobjective Programming Model with Trapezoidal Structure and Relations of Its Solutions [J]. Journal of Jilin University： Science Edition, 2011, 49(5)： 802-808. (张杰, 徐玲敏, 胡鼎. 具有梯形结构大系统目标规划模型的双向分解及解的关系 [J]. 吉林大学学报： 理学版, 2011, 49(5)： 802-808.)