锂离子电池温度场相似准则推导与有限元验证
2013-12-02程洪正张立军
程洪正,张立军,阮 丞,刁 坤
(1.同济大学 汽车学院,上海201804;2.同济大学 新能源汽车工程中心,上海201804)
动力电池是电动汽车的最核心部件之一.近年来,锂离子电池因其优异的综合性能倍受关注[1].工作温度对电池的各种特性,例如充放电功率与能量、效率、安全性、可靠性和寿命等都具有重要影响,并进而显著影响电动汽车的性能[1-3].因此,有关锂离子电池热动力学的建模与仿真、测试与评价、管理与控制成为核心关键技术[1-3].
方形锂离子电池的单电池结构主要由正负电极、隔膜和正负集流板组成,如图1所示.正负集流板、正负电极、隔膜的长度和宽度方向尺寸为分米级,而厚度方向尺寸为微米级,具有显著的跨尺度特征[1-2].
目前,采用有限单元方法进行电池内部温度场的建模与分析已经成为趋势[3].国内外相关研究主要基于对实际电池的不同程度简化假设,考虑不同的运行 工 况,建 立 起 一 维[4-6]、二 维[7]、三 维[8-9]温 度场模型.国内外学者建立的三维模型大多都将单体电池简化为由各向异性的单一材料组成的单层结构,假设电池为均匀的发热体或施加一致性热源[4-9].实际上,每个单体锂离子电池是包含上百个图1所示单电池的分层结构,且单电池的各层材料热学属性存在很大的差异,因而,在一定的工况下,内部温度场并非均匀分布.但是,若直接按照单电池多层结构的实际尺寸进行单元划分,进行电池内部温度场有限单元建模与计算,将会由于跨尺度原因产生模型单元数量多、计算量大、难以实现的严重困难.

图1 锂离子单电池结构示意图与三维尺寸(单位:mm)Fig.1 Schematic of lithium-ion battery cell(unit:mm)
因此,如何解决跨尺度建模问题成为利用有限元方法进行电池内部瞬态温度场的预测的关键.本文就是针对这一问题提出了一种基于相似理论的解决方法.
相似理论方法是人们在探索自然规律的过程中形成的一种常用的模化方法,对流体力学、传热学等学科的发展曾发挥了不可估量的作用[10],并在各种传热工程技术领域中得到广泛应用[11-12].然而,目前还未发现将相似理论应用于电池物理场的建模预测,以及解决锂离子电池跨尺度建模问题的案例.
为了解决电池内部温度场有限单元建模的跨尺度难题,本文提出了基于相似理论的动力电池内部瞬态温度场建模方法,从非稳态导热微分方程出发推导建立了温度场相似准则和相似关系,并利用ANSYS有限元软件进行了相似准则和相似关系正确性的验证,从而为面向对象的锂离子动力电池热动力学建模、分析与管理奠定了良好的基础.
1 温度场相似准则的推导
1.1 温度场相似准则
电池的生热散热过程是一个典型的三维、内热源的非稳态导热过程,为预测其温度场,建立了三维常物性、非稳态、第三类边界条件下的导热微分方程[13].
控制方程:
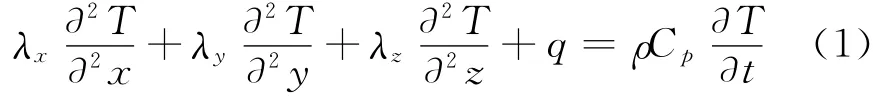
第三类边界条件:

初始条件:
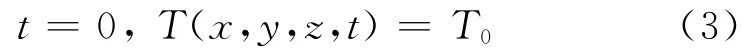
式(1)—(3)中:λx、λy和λz分别为x、y和z三个方向的热传导系数;T为温度;q为内热源功率密度分布函数;ρ为密度;Cp为定压比热容;t为时间;hx,hy,hz分别为x、y、z三个方向的对流换热系数;T0为初始温度;Tf为环境中流体的温度;a,b,c分别为x、y、z三个方向上的几何参数.
为将方程(1)—(3)作量纲一化处理,引入长度、时间、温度三个标尺.
x,y,z方向上长度标尺分别取为δx、δy和δz,分别为
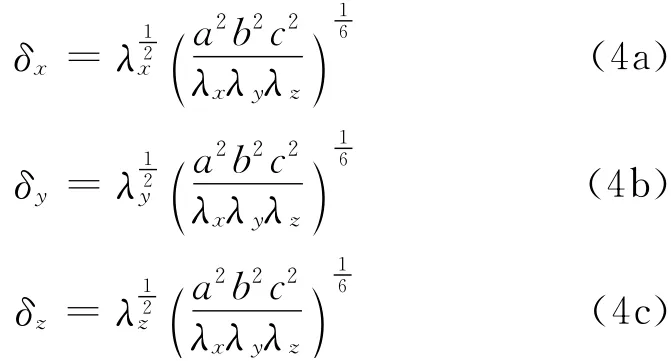
温度度标尺取为

式中:θ0为过余温度标度.
时间标尺取为

量纲一化导热微分方程为

第三类边界条件:
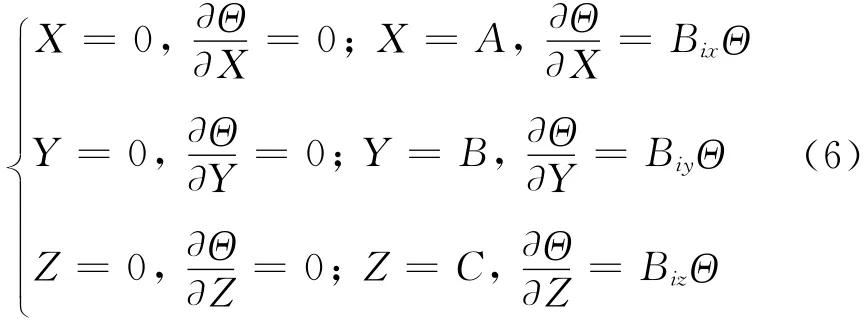
初值条件:

式(5)—(7)中:Θ=θ/θ0为量纲一温度,θ为过余温度为傅里叶数,表征量纲一时间;,为无量纲一生热速率和分别为x,y,z方向量纲一对流边界位置;为量纲一位置坐标为毕渥数,表征量纲一对流散热系数.
显然,由方程(5)—(7)可以看出,量纲一过余温度Θ为Bix、Biy、Biz、Fo、Q、X、Y、Z、A、B和C的函数.
以上即为三维常物性、非稳态、第三类边界条件下非稳态导热问题的相似准则数.
1.2 温度场原型与相似模型的参数设置
基于相似理论提出将厚度方向尺寸放大N倍的温度场相似模型.根据前面的分析,要实现温度场相似,相似准则数必须相等.由此确定相似模型与原型之间的参数设置必须满足如表1 所示的比例关系.表中,N为缩放的比例.

表1 模型参数设置比例关系(原型:模型)Tab.1 Parameters ratios of prototype to scale model
当满足表1条件时,模型与原型的温度场相似,即Θ1(X,Y,Z,Fo)=Θ2(X,Y,Z,Fo),也就是T1(x,y,z,t)=T2(x,y,Nz,t).
2 基于有限元的相似准则验证
2.1 单层结构的有限元计算与验证
文献[14]给出了将单电池五层结构简化为单层结构的等效方法,等效热传导系数、体积比热容等效计算公式如下:

式中:λi为单电池各层热传导系数;ci为各层厚度;ρCp为及体积比热容.
利用ANSYS软件分别建立原型和厚度方向放大2倍的相似模型,进行相似准则和相似关系的验证.由于单层结构厚度方向总尺寸为0.19mm,与长度宽度方向尺寸相差达到2个数量级.为此,分别将单层结构厚度方向放大100倍和放大200倍得到的单层结构模型作为原型和相似模型,根据相似准则设置参数,通过对比验证相似准则和相似关系的正确性.
建模时假设:
(1)单体电池四周对流换热,数值为10 W·m-2·K-1,顶面和底面的对流换热等分到每个单电池的顶面和底面上,数值为10/154≈0.065W·m-2·K-1,并忽略热辐射的影响.
(2)电池工作在1C 放电工况下,利用Bernardi等[15]提出的电池生热速率公式(11),计算得到单电池的均匀体生热速率为28 340 W·m-3.其中,生热速率计算公式如下:

式中:I为电流;V为电池体积;Eoc为电池平衡电压;U为电池工作电压;T为温度.
图2所示为原型和相似模型的瞬态热传导有限单元模型,模型的单元类型为solid90.其中,原型的单元总数为1 792个,相似模型的单元总数为3 360个.

图2 原型和相似模型热传导有限单元模型Fig.2 Finite element models of heat transfer
根据电池实际工况和相似准则,原型和相似模型的有限单元模型的属性参数设置见表2.

表2 有限元模型参数设置Tab.2 Parameters of finite element models
图3所示为3 600s时刻两种模型的温度场计算结果.图3a、图3b分别为原型和模型3 600s时刻温度空间分布图,图3c为原型和模型中对应测点的温度时间历程曲线.其中,原型角点(0,0,0),原型中心点(47,84,9.5),模型角点(0,0,0),模型中心点(47,84,19).
由图3计算结果可知,相似模型与原型的温度场的完全相似,即最高温度和最低温度,以及温度场的空间分布和时间历程的完全一致.这说明,理论推导确定的相似准则和相似关系是完全成立的.

图3 单层结构原型与相似模型计算结果对比Fig.3 Comparison of calculation results between prototype and scale model with single-layer structure
2.2 多层结构的有限元计算与验证
在多层结构假设条件下,利用ANSYS软件分别建立原型和厚度方向放大2倍的相似模型,进行相似准则和相似关系的验证.分别将原始结构厚度方向放大1 000倍和2 000倍得到的5层结构作为原型和相似模型,根据相似准则设置模型参数,通过对比有限元计算结果,验证相似准则和相似关系的成立.
图4所示为原型和相似模型的瞬态热传导有限单元模型,单元为solid90.其中,原型的单元总数为15 408个,相似模型的单元总数为30 816个.建模假设与单层结构相同.

图4 原型和相似模型热传导有限单元模型Fig.4 Finite element models of heat transfer
根据电池工况和相似准则,原型和相似模型的有限单元模型的属性参数及载荷、边界条件、初始温度设置见表3—5.
图5所示为3 600s时刻两种模型的温度场计算结果,其中图5a、图5b 分别为原型和相似模型3 600s时刻的温度分布,图5c为原型和模型对应测点的温度—时间历程曲线.对应测点的位置坐标见表6.
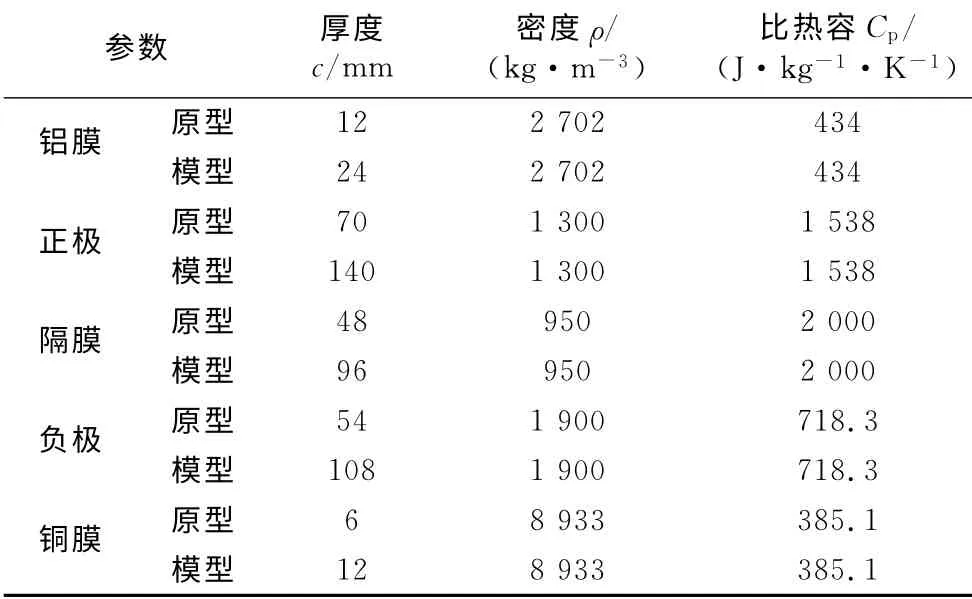
表3 有限元模型参数设置一Tab.3 Parameters of finite element models:part 1
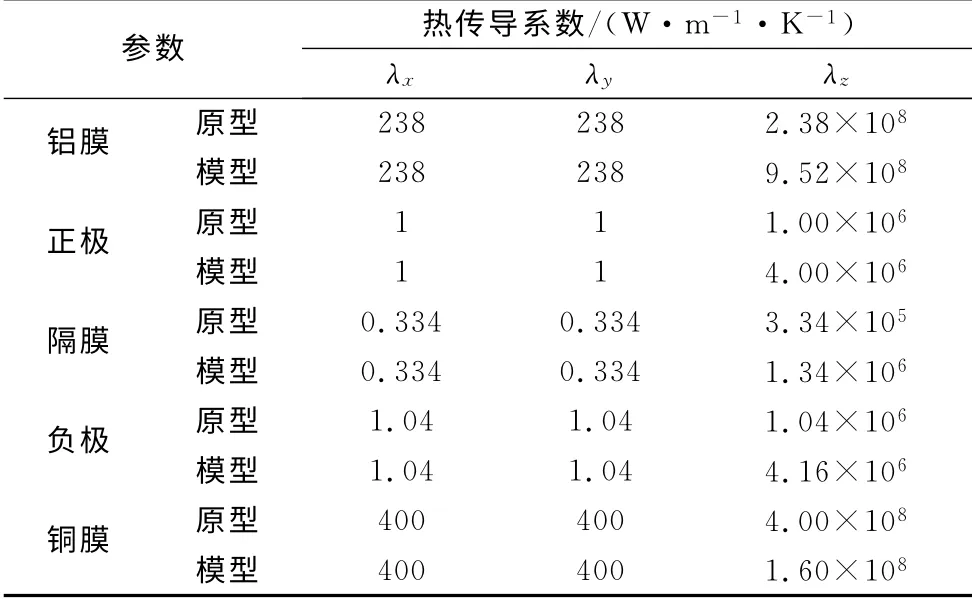
表4 有限元模型参数设置二Tab.4 Parameters of finite element models:part 2
由图5可知,相似模型与原型整体最高温度相差0.004 ℃,最低温度相差0.046 ℃,推测是由于有限元计算误差所致.因此,若忽略有限元计算误差,在厚度方向放大2倍后,相似模型与原型的温度场相似,即最高温度和最低温度,以及温度场的空间分布和时间历程一致.这说明,理论推导确定的相似准则和相似关系成立,而且可以满足复杂的多层结构的建模与分析.

图5 五层结构原型与相似模型计算结果对比Fig.5 Comparison of caculation results between prototype and scale model with multi-layers structure
3 结论
本文针对锂离子电池多层跨尺度的相似模型建模研究主要得到以下结论:(1)根据三维常物性、非稳态、第三类边界条件下导热微分方程,通过量纲—分析得到的相似准则和相似关系完全能够实现温度场时间历程和空间分布的一致模拟;(2)在某一方向几何尺寸缩放N倍,为实现温度场完全相似,相应方向的热传导系数相应缩小N2倍,而对流换热系数则缩小N倍,其他保持不变.
虽然本文已经基于相似理论建立了锂离子电池内部温度场的建模与预测方法,但是后续仍需通过大量的试验修正模型参数,在进一步验证有效性的基础上,提高模型的预测精度.
[1] Keyser M,Mihalic M,Pesaran A.Thermal characterization of plastic lithium ion cells[M]//The 18th International Seminar and Exhibit on Primary and Secondary Batteris. Fort Lauderda:Advanced Battery Technology,2001.
[2] Chen S C,Wan C C,Wang Y Y.Thermal analysis of lithiumion batteries[J].Journal of Power Sources,2005,140(1):111.
[3] 李腾,林成涛,陈全世.锂离子电池热模型研究进展[J].电源技术,2009,33(10):927.LI Teng, LIN Chengtao, CHEN Quanshi. Research development on lithium-ion battery thermal model[J].Chinese Journal of Power Sources,2009,33(10):927.
[4] Pals C R,Newman J.Thermal modeling of the lithium/polymer battery:I.discharge behavior of a single cell[J].Journal of the Electrochemical Society,1995,142(10):3274.
[5] Pals C R,Newman J.Thermal modeling of the lithium/polymer battery:II.temperature profiles in a cell stack[J].Journal of the Electrochemical Society,1995,142(10):3282.
[6] Smith K,Wang C Y.Power and thermal characterization of a lithium-ion battery pack for hybrid-electric vehicles [J].Journal of Power Sources,2006,160(1):662.
[7] Chen Y,Evans J W.Heat transfer phenomena in lithium/polymer-electrolyte batteries for electric vehicle application[J].Journal of the Electrochemical Society,1993,140(7):3274.
[8] Chen Y,Evans J W.Three-dimensional thermal modeling of lithium-polymer batteries under galvanostatic discharge and dynamic power profile[J].Journal of the Electrochemical Society,1994,141(11):2947.
[9] Taheri P,Bahrami M.Temperature rise in prismatic polymer lithium-Ion batteries:an analytic approach[C]//Proceedings of SAE2012 World Congress &Exhibition.Detroit:SAE 2012 World Congress &Exhibition.2012:164-176.
[10] 王丰.相似理论及其在传热学中的应用[M],北京:高等教育出版社,1990.WANG Feng.Similarity theory and its application in heat transfer theory[M].Beijing:Higher Education Press,1990.
[11] 蔡志鹏,鹿安理,史清宇,等.相似理论在焊接温度场和应力场及应变场中的应用[J],焊接学报,2000,21(3):79.CAI Zhipeng,LU Anli,SHI Qingyu,et al.Application of similitude principles to study in welding temperature,strain and stress fields[J].Transactions of the China Welding Institution,2000,21(3):79.
[12] 朱作京,于达,宫敬.储油罐温度场模拟过程中传热相似理论[J].油气储运,2007,26(12):37.ZHU Zuojing,YU Da,GONG Jing.Study on thermal-like theory in simulation process of temperature field of oil storage tank[J].Oil &Gas Storage and Transportation,2007,26(12):37.
[13] 杨世铭,陶文铨.传热学[M].北京:高等教育出版社,2008.42-45.YANG Shiming,TAO Wenquan.Heat transfer theory[M].Beijing:Higher Education Press,2008.42-45.
[14] Bandhauer T M,Garimella S,Fuller T F.A critical review of thermal issues in lithium-ion batteries [J].Journal of the Electrochemical Society,2011,158(3):1.
[15] Bernardi D,Pawlikowski E,Newman J.A general energy balance for battery systems[J].Journal of the Electrochemical Society,1985,132(1):5.
