盾构隧道开挖引起既有管线的竖向变形
2013-12-02张子新
张 桓,张子新
(1.同济大学 岩土及地下工程教育部重点实验室,上海200092;2.同济大学 地下建筑与工程系,上海200092)
盾构隧道的施工将不可避免地对邻近地下管线产生影响.在分析盾构隧道开挖引起的邻近管线的变形和内力时,理论解析方法概念明确,可方便快捷地为工程实际提供一定的指导性建议.目前,国内外学者在采用理论解析方法分析隧道开挖对邻近既有管线的影响时,通常采用的是两阶段分析方法,即在第一阶段分析隧道开挖引起的既有管线轴线位置处的土体自由位移场,第二阶段则将第一阶段求得的土体位移施加于管线,并基于弹性理论方法或者Winkler地基模型来求解管线的变形和内力.基于Winkler地基模型的方法由于使用简单而被广泛采纳,如Attwell等[1]、Vorster等[2]以 及Klar等[3]众多学者对此进行了研究.但基于Winkler地基模型的两阶段解析方法仍有一些问题值得探讨:
(1)第一阶段中通常采用Peck经验公式预测隧道开挖引起的管线轴线处的土体位移,这并不可靠[4].(2)Winkler地基模型把地基模拟为刚性底座上一系列独立的弹簧(图1a),图中,q(x)为作用在管线上的附加应力,EI为管线刚度,kw和k为弹簧刚度系数,G为剪切刚度,由弹簧刚度kw来控制地基变形[5].由于没有考虑地基连续性,Winkler地基模型往往不能全面地反映地基的实际情况,特别对于密实厚土层地基和整体岩石地基,将会引起较大的误差[6].(3)盾构隧道开挖对管线的影响是一个典型的三维问题,而已有的解析公式在推导时从平面应变问题出发,忽略了管线侧向土体对管线的作用,这必然影响计算结果的准确度.
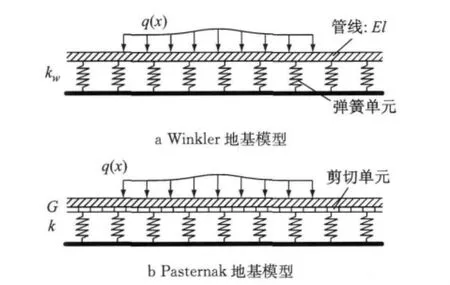
图1 两种典型地基模型示意图Fig.1 Two typical foundation model schemes
针对问题(1),王涛等[4]以及张治国等[7]均认为采用Loganathan等[8]提出的解析解计算第一阶段隧道开挖引起的土体自由位移更加可靠.
针对问题(2),为了克服Winkler地基模型的固有缺陷,人们对Winkler地基模型进行了发展,开发了双参数地基模型.双参数地基模型的发展沿着两个不同方向进行,第一种是通过在Winkler地基模型的各个弹簧之间提供力学的相互作用以消除其不连续性,如Pasternak模型[9](图1b);第二种则是以弹性连续介质模型为基础并引入约束或简化位移分布与应力的假设,如Reissner 模型及Vlasov 模型[6].Kerr[10]在 对 比 了 多 种 地 基 模 型 后 指 出,Pasternak地基模型是对Winkler地基模型最合理的拓展且具有比Winkler模型更高的精度.
针对问题(3)的讨论目前很少.盾构隧道开挖对管线的影响实质是一个三维的空间问题,由于地下管线埋深一般较浅,且隧道开挖方向与管线走向垂直时,管线的受力情况最为不利[6],这里仅对此情形进行分析(图2).一般而言,在没有管线的情况下,盾构隧道推进引起的垂直于隧道轴线的土体位移当如曲面A′B′CD的形状所示,可以视作平面应变问题进行求解.当有管线存在时,管线会限制周围土体的变形,因而土体变形会较无管线时小.传统基于Winkler地基模型的弹性地基梁法均将此问题简化为平面应变问题进行处理,相当于认为在有管线存在的情况下,管线侧向土体发生与管线底部土体相同的位移,整个管线层面处的土体变形如曲面ABCD的形状所示,这种简化显然并不符合实际.实际情况是,管线的存在不仅会约束其底部土体,也会对其侧向一定范围内的侧向土体产生约束作用,导致这部分侧向土体产生比无管线存在时更小的位移;而离开管线更远处的侧向土体则由于离开了管线的影响范围,其竖向位移的大小应和无管线存在时的情况一样,整个管线层面处的实际土体变形应如曲面AB′CD的形状所示.反过来,因为管线的约束作用,管线侧向土体会对管线产生反作用力,这种影响不可忽略.
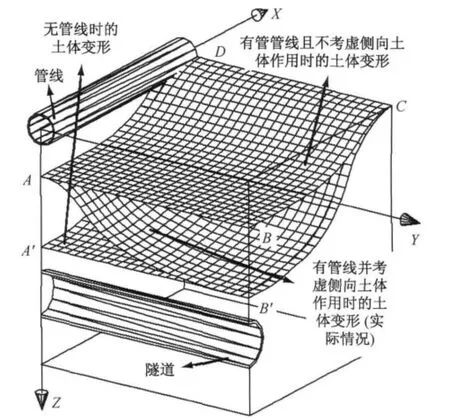
图2 盾构隧道开挖对既有管线影响的三维空间示意图Fig.2 3Dschematic diagram for effects of shield tunneling on the existing pipeline
综上所述,本文采用两阶段分析法,第一阶段采用Loganathan公式计算盾构隧道开挖引起的土体自由位移,第二阶段将管线视作Pasternak双参数地基上的无限长梁,将求得的土体自由位移施加于管线,建立并求解管线的竖向受荷变形平衡微分方程,从而得到管线竖向变形和内力的计算表达式.进一步考虑盾构隧道开挖时管线侧向土体对管线的约束作用,得到了更符合实际的解.基于简化弹性空间法获得的地基参数,将Pasternak地基和Winkler地基的解析计算结果与数值计算结果以及工程实例监测数据进行对比验证,证明了Pasternak地基模型的优越性和本文计算方法的有效性.
1 隧道开挖引起的土体自由位移
1.1 管线受力模型的假定与简化
首先按照传统的思路,从平面应变问题出发探讨不考虑侧向土体作用时隧道开挖对既有管线的影响,在xoz平面内进行讨论(图2).本文的研究基于Attewell[1]推导传统Winkler模型方法时所提出的基本假设:①管线与土体为连续均质弹性体;②管线与周围土体始终保持接触;③管线的存在不影响隧道的开挖;④隧道的存在不影响管线轴线处土体的受力响应.简化计算模型如图3所示.图中R为隧道半径,z0为既有管线轴线深度,h为隧道轴线深度,D为管线直径.
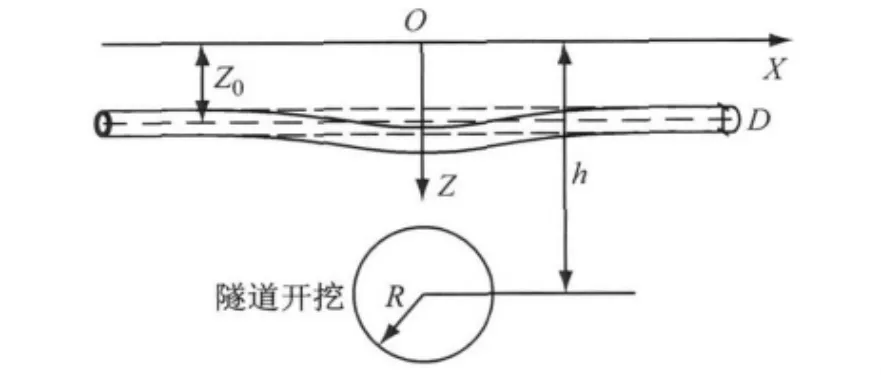
图3 隧道开挖对既有管线影响的简化计算模型Fig.3 Simplified model for effects of shield tunnelling on the existing pipeline
1.2 隧道开挖引起的土体自由位移
Loganathan等[8]提出了自由场地时隧道开挖引起的既有管线轴线位置处土体沉降u(x)为
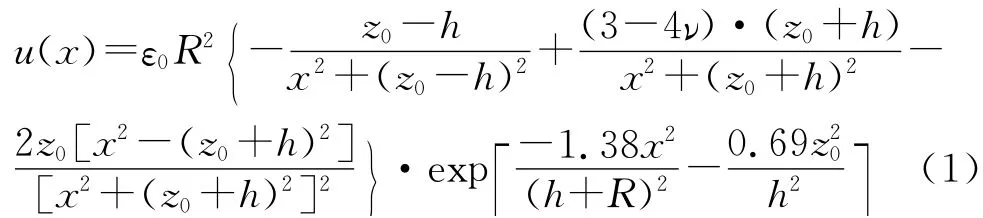
式中:ν为土体泊松比;ε0为平均地层损失比;x为距隧道中心线的水平距离.
1.3 作用于管线轴线上的附加应力
Pasternak地基模型(图1b)包含了一个弹簧层以及一个剪切层,则作用在管线上的附加应力为
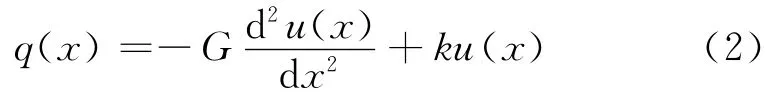
2 Pasternak地基上管线变形解析解
2.1 不考虑侧向土体作用的管线平衡微分方程
假设因隧道开挖作用导致的管线挠度为w(x),管线应力为p(x),k为地层系数,则有:
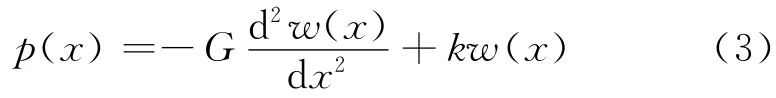
假设管线的直径为D,则管线受荷的平衡微分方程为
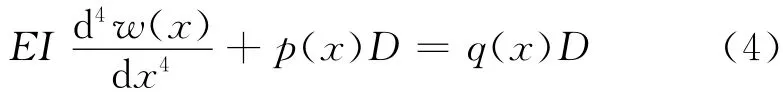
将式(3)代入式(4)并整理得:
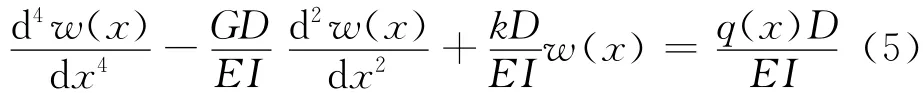
2.2 微分方程的通解
为求解方程(5),先求其通解.令q(x)=0,得:
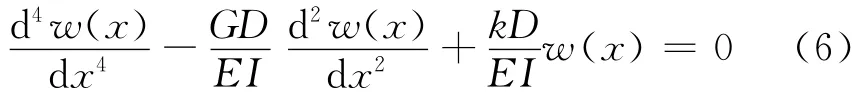
式(6)的特征方程为
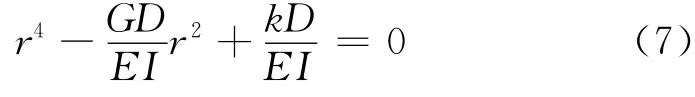
式(7)的解与Δ的符号相关,其中:

(1)当Δ>0,即:G2D>4kEI时,有:

因此,管线变形w(x)可表示如下:

式中:A1,A2,B1,B2为待定系数.
(2)当Δ=0,即:G2D=4kEI时,有:

因此,管线变形w(x)可表示如下:

(3)当Δ<0,即:G2D<4kEI时,有:
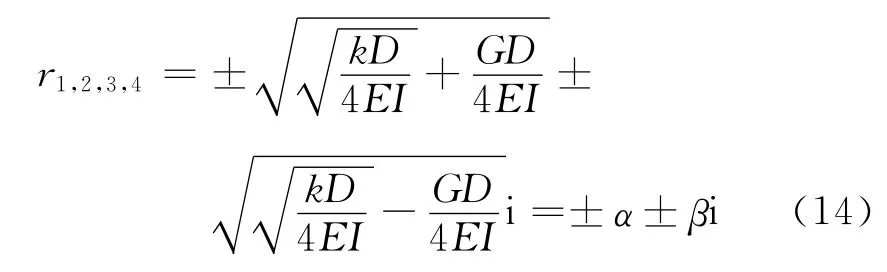
因此,管线变形w(x)可表示如下:
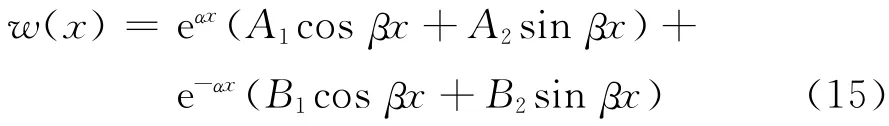
2.3 集中荷载作用下微分方程的解
为了求解隧道开挖对上部管线的影响,先求解Pasternak 地基上管线受集中荷载作用时的解(图4).图中,P为集中荷载.
利用该问题的对称性,针对x≥0的部分进行研究.当x趋近于+∞时,w=0,故w(x)可化简为此时,方程(5)的特解为w*=0.同时,有边界条件如下:通过边界条件(17)即可解出w(x)的表达式如下:
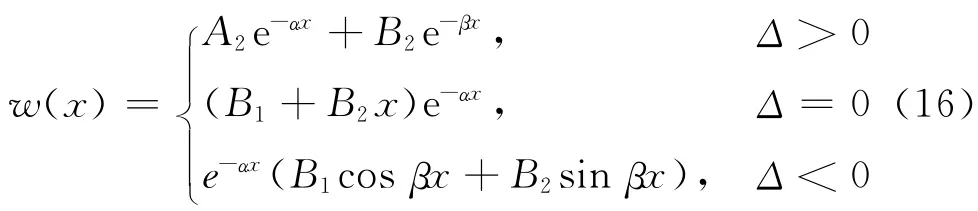


式中:
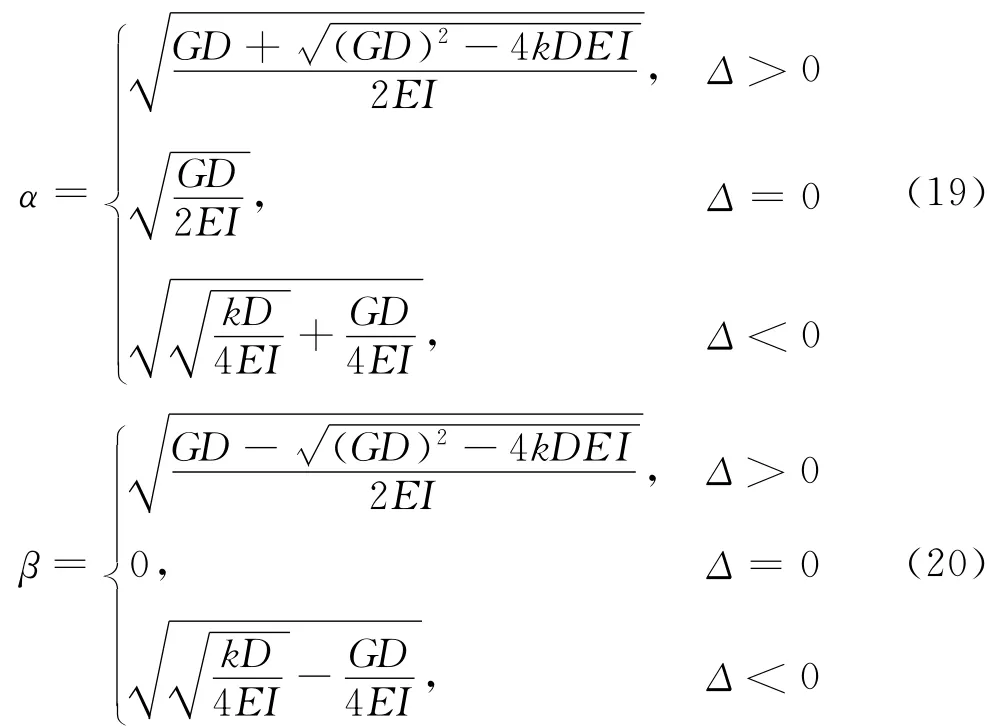
于是,管线纵向弯矩的表达式为

2.4 隧道开挖引起管线的竖向变形
假定在隧道开挖的影响下,管线轴线(x轴)上任意一点ξ上作用的附加荷载为q(ξ)dξ,则根据式(18),该荷载引起管线轴线上任意点x的位移dw(x)为
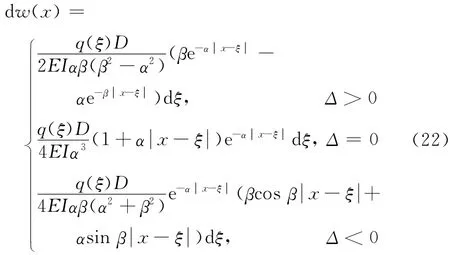
对式(22)在管线附加荷载分布范围内积分,即可得到由于隧道开挖而引起的管线的竖向变形:

3 考虑侧向土体作用时的管线变形
3.1 管线受荷变形平衡微分方程
以上讨论仅考虑了管线下部土体对管线的作用,为了得到更为符合实际情况的结果,此处进一步考察管线侧向土体对管线的作用.同样,基于Pasternak地基模型,首先推导管线与侧向土体共同受集中荷载P-作用时的管线变形与内力(如图5a,P为仅作用于管线的集中荷载).为简化起见,对模型做如下假定:①管线侧向土体与底部土体参数相同;②侧向土体对管线的作用力作用于管线两侧,并沿x方向分布(如图5b).图中F(x)即为侧向土体对管线的作用力.
考虑任意与yoz平面平行的x=X平面,对于y≥D/2部分的侧向土体,假设土体位移为w-(y),则其平衡方程为

方程(24)的通解为

假设距离管线足够远处y=Y平面的土体变形,则为方程(24)的特解.那么方程(24)的解为

根据边界条件:在x=X平面内,y=D/2处,侧向土体与管线下方土体变形相等,即:

将式(26)代入式(27)可得:
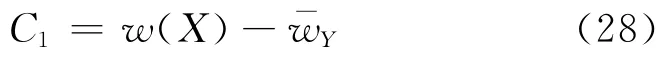
因此:

则在x=X平面内,侧向土体对管线的作用力为

在y=Y平面内求解.对于x≥0的土体,其平衡方程为
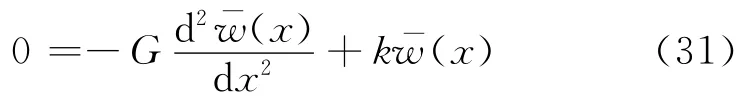
方程(31)的解为
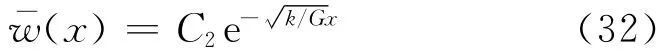
利用边界条件:当x=0时,有:
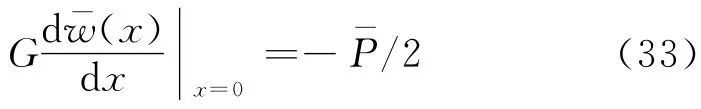
解得:
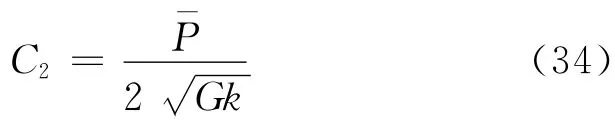
因此:

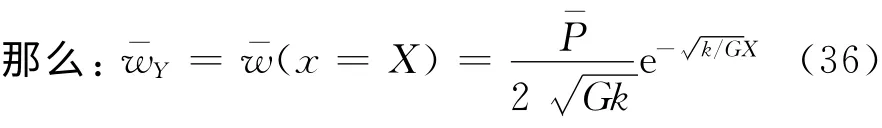
结合式(30)与式(36)可知,侧向土体对管线的作用力为
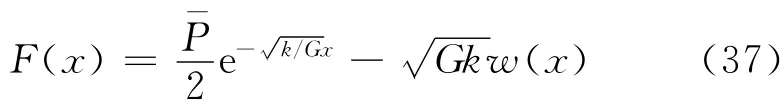
在集中荷载作用下,并考虑侧向土体对管线的作用时,管线的平衡微分方程为

将式(3)与式(37)代入式(38),得:
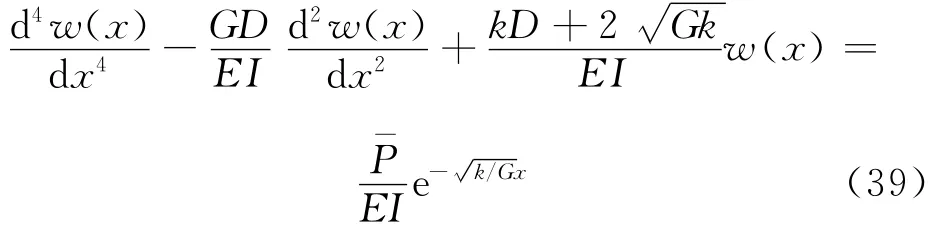
3.2 微分方程的解
式(39)式具有形式如下的特解:
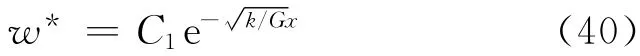
代入方程(39)可解得:
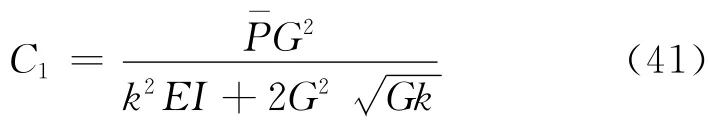
根据式(5)的通解求解过程,同理可解得式(39)的通解.按照式(23)积分即可得到最终考虑侧向土体作用时由盾构隧道开挖引起的管线竖向变形.
4 算例验证
为了检验本文方法是否能够更好地反映管线的受力变形情况,将基于Pasternak 地基模型和Winkler地基模型得到的管线变形与弯矩分别与更为精确的数值计算结果以及工程实际监测数据进行对比验证.
Winkler地基上管线受荷的平衡微分方程为

集中荷载作用下Winkler地基的解为
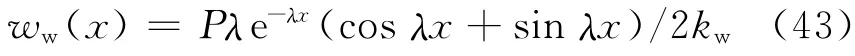
其中:
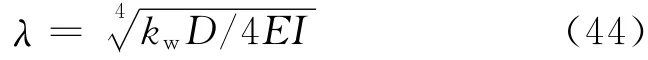
按照式(23)积分即可得到由盾构隧道开挖引起的管线竖向变形.
在采用弹性地基模型时,模型参数的取值是个很重要的问题.地基模型参数的获取方法有多种,目前,通过引入简化条件直接从弹性连续体方程推导出地基参数的简化弹性空间法由于概念清晰,操作简便,得到了越来越多的应用.根据简化弹性空间法,Pasternak地基的参数k、G以及Winkler地基的参数kw的值分别为[11]:k=E0/H,G=G0H/2;kw=E0/H.其中:G0=E0/2(1+ν),H为管线下方地基厚度.H是一个比较难确定的参数,根据徐凌[12]对基础底部附加应力随地基深宽比变化的研究,对于长宽比很大的基础(对应管线这种长度与直径比很大的类型),当地基深宽比大于6时,其基底附加应力已衰减至非常小.因此,本文计算中取管线下方地基厚度为6D.
4.1 与数值计算结果的对比
以上海地铁11号线盾构施工中所穿越的一条直径D=1m,壁厚t=0.12m 的混凝土水管为计算对象进行分析,所采用的参数见表1.表中,R、h、z0、ε0、D和EI根据工程实际参数取值,土体弹性模量E0和泊松比ν根据各土层厚度加权平均后得到,管线下方地基厚度H取6D.数值分析采用ABAQUS程序对相同工况进行有限元模拟,并将Pasternak方法和Winkler方法的解析结果与更为精确的数值结果进行对比.

表1 水管计算参数表Tab.1 Calculation parameters of a water pipeline
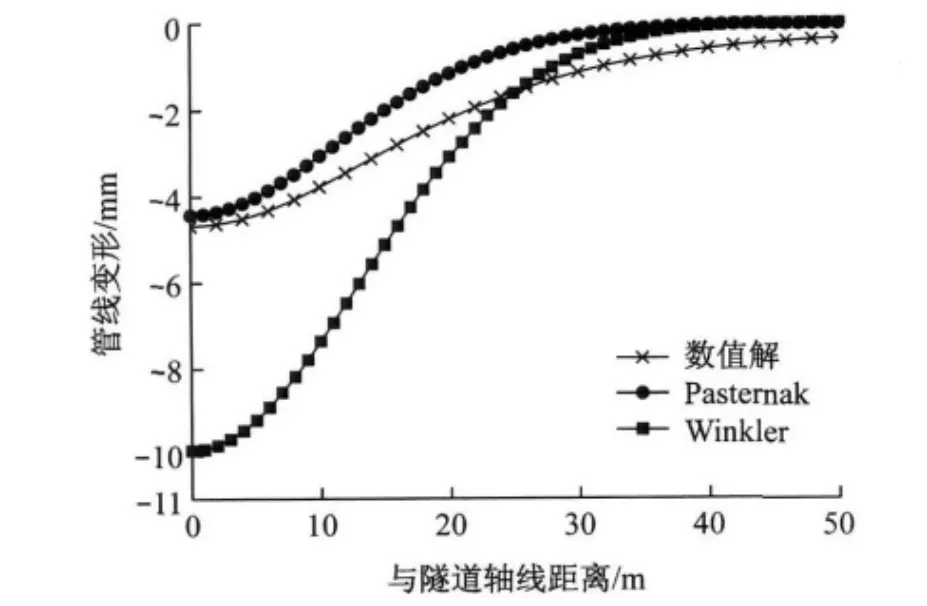
图6 管线变形Fig.6 Pipeline deformation
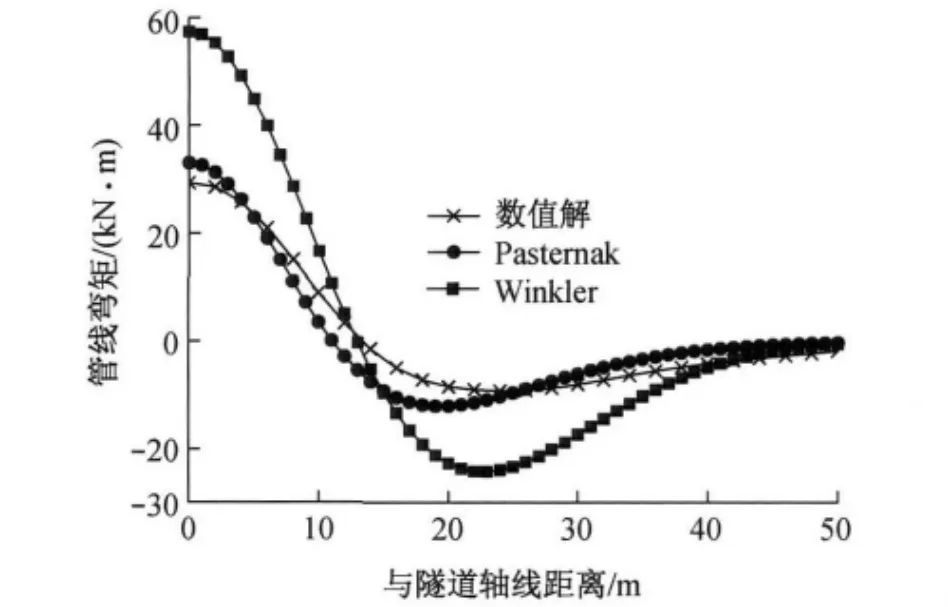
图7 管线弯矩Fig.7 Pipeline moment
两种地基模型下的管线变形以及弯矩分布与有限元模拟结果的对比见图6—7.显而易见,相对于Winkler地基而言,Pasternak地基上的管线变形和弯矩分布均更贴近于数值计算的结果.如果定义:偏差=(解析解-数值解)/数值解,则Pasternak地基上管线的最大变形和最大弯矩与有限元结果的偏差分别为-5.5%与-12.7%,而Winkler地基上管线的最大变形和最大弯矩与有限元结果的偏差则分别为110.7%和95.7%.因此,Pasternak地基模型能更准确地反映管线的实际受力和变形情况,而Winkler地基由于无法考虑地基弹簧之间的联系,所得结果与实际相差较大.
4.2 工程实例验证
深圳地铁一期工程益田站至香蜜湖站区间隧道全长约1 540m,采用两台土压平衡盾构机分别进行左右线隧道的施工.隧道轴线埋深为12.0~15.0 m.盾构机刀盘外径为6 190mm,盾壳外径为6 140 mm.隧道外径为6 000mm,隧道内径为5 500mm.盾构在里程RK8+750处近距离垂直下穿一条大管径电缆管线,管线材质为混凝土.管线外径为3.0 m,壁厚0.12m,埋深7.2m[13].
根据表2 所示的计算参数,采用本文方法、Winkler地基模型方法以及未考虑侧向土体作用时的Pasternak地基模型方法计算得到了隧道开挖引起的管线变形,并将其与文献[13]中的实际监测数据进行对比,如图8所示.可以看到,相对于Winkler地基模型以及未考虑侧向土体作用时的Pasternak地基模型方法而言,采用本文方法预测的管线最大沉降和隧道开挖对管线的影响范围均更加准确,再次验证了本文方法的有效性.

表2 工程实例计算参数表Tab.2 Case study calculation parameters
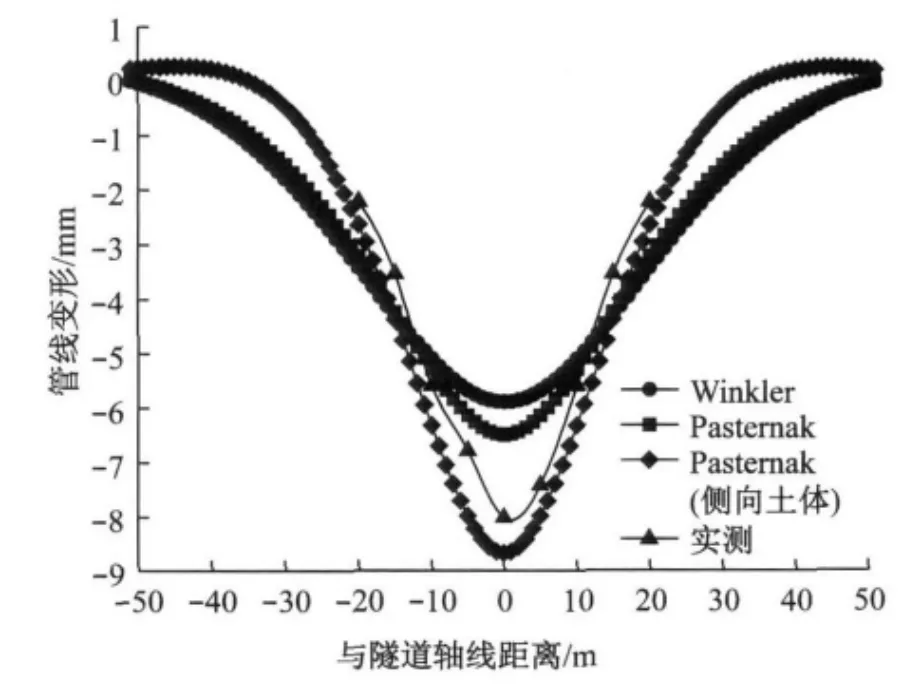
图8 盾构隧道开挖作用下的管线变形Fig.8 Pipeline deformation due to shield tunnelling
5 结语
(1)采用两阶段法计算盾构隧道开挖对管线的影响是一种意义明确的简化计算方法,只要选择合适的土体自由位移计算公式和地基模型就能较好地反映工程实际情况.
(2)由于Pasternak双参数地基模型考虑了弹簧之间的相互作用,采用Pasternak地基模型计算隧道开挖对于地下管线的影响较传统的Winkler地基模型更为准确.
(3)使用简化弹性空间法获得地基参数较为简便,本文方法的计算结果对地基厚度H和管土弹性模量比E/E0的变化均较为敏感,而泊松比ν的变化对结果影响较小.
(4)管线侧向土体对管线的约束作用比较显著,在计算管线变形时应该加以考虑,能够使计算结果更贴近真实情况.
(5)本文方法是对传统的基于Winkler地基模型方法的改进和补充,同样只是针对隧道开挖对管线影响问题的一种近似解.这种近似对于盾构隧道正常施工,管线周围土体绝大部分土体处于弹性状态的实际工况而言是合理和可接受的.但对于盾构施工造成的土体损失过大,隧道周围的土体大量进入塑性状态且塑性区发展至管线周围土体,则不推荐使用本文方法.
[1] Attwell P B,Yeates J,Selby A R.Soil movements induced by tunneling and their effects on pipelines and structures[M].London:Blackie &Son Ltd,1986.
[2] Vorster T E B,Klar A,Soga K,et al.Estimating the effects of tunneling on existing pipelines[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,131(11):1399.
[3] Klar A,Vorster T E B,Soga K,et al.Soil-pipe interaction due to tunnelling:comparison between Winkler and elastic continuum solutions[J].Geotechnique,2005,55(6):461.
[4] 王涛,魏纲,徐日庆.隧道开挖对邻近地下管线的影响预测分析[J].岩土力学,2006,27(增刊):483.WANG Tao,WEI Gang,XU Riqing.Prediction for influence of tunneling on adjacent pipelines[J].Rock and Soil Mechanics,2006,27(Supplement):483.
[5] Winkler E.Die lehre von der elastizitat und festigkeit[D].Prague:[s.n.],1867.
[6] A P S Selvadurai.Elastic analysis of soil-foundation interaction[M].New York:Elsevier Scientific Publishing Company,1979.
[7] 张治国,黄茂松,王卫东.邻近开挖对既有软土隧道的影响[J].岩土力学,2009,30(5):1373.ZHANG Zhiguo, HUANG Maosong, WANG Weidong.Responses of existing tunnels induced by adjacent excavation in soft soils[J].Rock and Soil Mechanics,2009,30(5):1373.
[8] Loganathan N,Poulos H G.Analytical prediction for tunnelinginduced ground movements in clays [J].Journal of Geotechnical and Geoenvironmental Engineering,1998,124(9):846.
[9] Pasternak P L.On a new method of analysis of an elastic foundation by means of two-constants [D]. Moscow:Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu I Arkhitecture,1954.
[10] Kerr A D.Elastic and viscoelastic foundation models [J].Journal of Applied Mechanics,1964,31:491.
[11] Kerr A D. On the determination of foundation model parameters[J].Journal of Geotechnical Engineering,1985,111(11):1334.
[12] 徐凌.软土盾构隧道纵向沉降研究[D].上海:同济大学土木工程学院,2005.XU Ling.Research of the longitudinal settlement of soft soil shield tunnel[D].Shanghai:College of Civil Engineering of Tongji University,2005.
[13] 吴为义.盾构隧道周围地下管线的性状研究[D].杭州:浙江大学建筑工程学院,2008.WU Weiyi.Study on mechanical behaviors of buried pipelines induced by shield tunneling construction [D].Hangzhou:School of Municipal Engineering of Zhejiang University,2008.
