台风“梅花”近地风剖面变化
2013-12-02王旭,黄鹏,顾明
王 旭,黄 鹏,顾 明
(同济大学 土木工程防灾国家重点实验室,上海200092)
统计表明,每年台风经过我国东南沿海地区都会对该地区造成大量人员伤亡和经济财产损失,其中由于低矮房屋损毁造成的损失占50%以上[1].为减轻风灾损失,掌握强风作用机理,本课题组在上海浦东近海岸边建立了同济大学风工程实测基地,该系统主要包括一座足尺低矮建筑及两座测风塔,用于对该地区风场特性以及低矮建筑屋盖风压特性进行研究[2].
在估算风对结构的作用力时,只有风特性参数模型得到比较准确的定义和模拟,风荷载计算才有较高的精度[3].因此,通过现场实测研究认识近地风沿高度的变化规律、风的湍流特性和近地面空气动力学参数是十分必要的.近些年,我国的近地强风特性现场实测研究取得了一些研究成果.顾明等[4-5]基于安装在上海环球金融中心494m 高度处风速采集仪所采集的风速数据,对平均及脉动风速特性进行了系统研究.李秋胜等[6]利用中国科学院大气物理研究所325m 高铁塔上所获得的在15层不同高度风速、温度资料,研究了北京地区320m 以下大气边界层的风特性,重点分析了平均风速和湍流度随高度的变化规律.戴益民等[7]基于多个台风实测数据研究了10m 以下高度平均风速和湍流度随高度的变化.相比于部分发达国家,我国近地强风的研究仍然较少,而受到试验条件的限制,基于台风实测数据的我国东南沿海地区近地风剖面的研究就更加匮乏,但这项工作对于结构风工程却意义重大.因此,本文基于40m 测风塔上10、20、30和40m 高度处的风速仪记录的台风“梅花”实测数据,研究了平均风速、湍流度和阵风因子随高度的变化规律,研究成果将为今后东南沿海地区建筑抗强风设计提供参考.
1 现场实测概况
1.1 台风“梅花”实测
2011年第9号热带风暴“梅花”(‘Muifa’)具有强度变化多、移动速度慢、移动路径不确定性大、生命史长等特点.“梅花”影响期间,台风中心离观测点最近距离250km,沿大陆近海向北以15km·h-1的速度移动,七级风圈半径400km,10 级半径120 km,风向偏北.台风路径和观测地点及测风塔实物如图1所示.

图1 台风“梅花”路径及测风塔实物图Fig.1 Track of typhoon‘Muifa’and photo of tower
1.2 试验仪器及设备
测风塔为格构式钢结构自立塔,塔高40 m,位于北纬31°11′46.36″东经121°47′8.29″,紧邻临海泵站入海口处.利用风速仪对整个台风过程中浦东近海地区近地层风速、风向、温度等信息进行了全程记录,记录时段为2011年8月6日2时8分至2011年8月7日19时40分.根据我国规范[8]中的规定,本文实测数据均按10 min基本时距分割成独立的子样本进行分析,风速及风向的变化及样本选取,以及风速仪安装及布置等相关内容已在文献[9-10]中详细给出,本文不再累述.
2 数据处理方法
2.1 平均风剖面模型
(1)指数率模型
Davenport在大量观测资料的基础上,对不同地貌下的风速剖面进行了整理分析,指出平均风速沿高度的变化可以用指数函数进行描述,表达式如下:
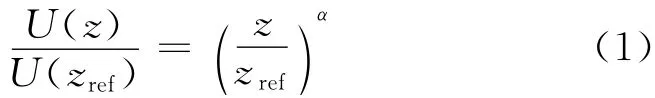
式中:z为高度;U(z)为z高度处的风速;zref为参考高度;U(zref)为参考高度处的平均风速;α表示地面粗糙度指数.
(2)对数率模型
根据大气边界层相似理论,边界层分为近地层和外层两部分.在两部分的重合区域,壁面定律和速度亏损定律同时成立,则得到风剖面的对数律表达式如下:
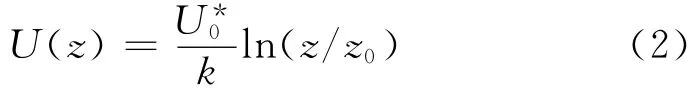
式中:k表示Karman常数,一般取表示摩擦速度,其中u′、v′和w′分别表示纵向、横线和竖向脉动风速(上划线表示均值,下同);z0为粗糙度长度,由于局部气流的不均一性,不同测试中的结果相差较大.因此,一般采用规范规定的经验数值.本文中实测地点周边的地貌特征符合美国规范[11]中C类场地条件,按照其规定z0取0.02m.
与指数率不同,对数率是在考虑边界层内流动特性的基础上通过推导得到,因此更加严谨.但需要注意,式(2)只适用于中性大气边界层内[12-13],根据莫宁-奥布霍夫相似性原理,可以得到更一般的形式:

式中:L为莫宁-奥布霍夫长度;Ψm是z/L的普适函数,表示大气的稳定程度,在不同的大气层结条件下,Ψm(z/L)有具体的表达形式.中性大气状态下,莫宁-奥布霍夫长度趋于无限长,此时Ψm(z/L)趋于0,式(3)即退化为式(2).因此,在利用对数率模型即式(2)对风速剖面进行分析时,首先要判断大气层结的状态,即是否接近中性层结.目前较为常用的判断方法有两种,分别为大气稳定性参数z/L判定法[6,14]和理查德森数Ri判定法[14-16].虽然两种方法在形式上有所不同,但本质相近,并且两者之间可以相互转化[17].所以,本文只采用z/L判定法对大气层结进行判断,其表达式及判定标准如下:

式中:g表示重力加速度,T表示位温的平均值,T′表示脉动位温,表示地表热通量.当z/L≤0.1时,可判定大气层结为中性.
(3)Deaves-Harris模型
Deaves-Harris模型是在对数率模型基础上的一种改进,它克服了对数率只能在边界层近地面区域成立的弱点,可以对全部边界层进行准确的描述[18-19],其表达式为

式中,zg表示边界层高度,表达式为:

其中,B′为经验参数,一般取6;f表示科里奥力参数,取为7.554×10-5s-1.
对于300m 以下中性大气层,式(5)可以简化为
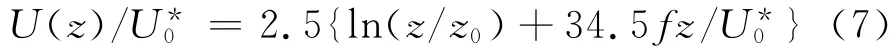
2.2 湍流度
湍流强度是衡量湍流强弱的相对指标,是确定结构风荷载的重要参数之一.定义为平均时距内脉动风速的标准差σ与相应时距内纵向平均风速大小U的比值,表达式为

式中:σi为脉动风速u(t)、v(t)和w(t)的均方根;u,v,w分别表示纵向、横向及竖向脉动风速分量.
2.3 阵风因子
阵风因子定义为阵风持续期tg内的平均风速最大值与相应平均时距内的平均风速U之比,表达式为

式中:Gu(tg)、Gv(tg)、Gw(tg)分别表示表示纵向、横向及竖 向 阵 风 因 子;max(u-(tg))、max(v-(tg))和max(w-(tg))分别表示纵、横及竖向脉动风在平均时距内阵风持续时间tg内平均最大风速.本文中阵风持续期tg取3s,平均时距取10min.
3 实测数据处理
3.1 平均风剖面模型参数
3.1.1 边界层高度zg
许多国家的规范均给出了不同地貌条件下边界层高度的建议值,认为边界层高度只与地表粗糙程度有关.但研究表明,风速的大小以及大气稳定程度都会对边界层高度产生影响.利用式(6)计算得到了边界层高度随平均风速的变化关系(图2).可以看到,利用式(6)计算得到的边界层高度随平均风速的增大而增大,平均值约为2 063m,远远大于我国规范[8](GB50009—2001,2002)规定的B 类地貌下的边界层高度(350m),但与文献[14]和文献[15]计算所得结果相近.
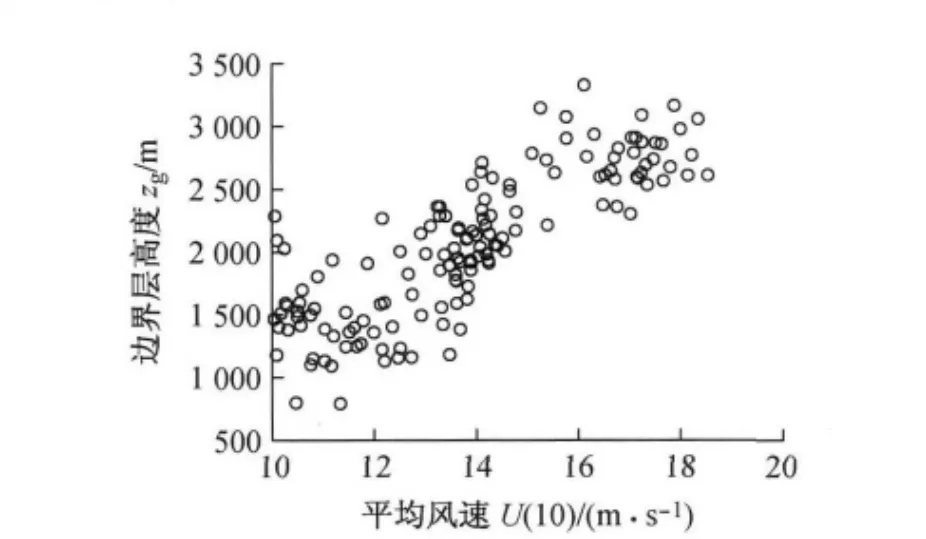
图2 边界层高度随10m 高度平均风速的变化Fig.2 The height of neutral atmospheric boundary layer versus the mean wind speed at the height of 10m
3.1.2 大气稳定度参数图3—5分别给出了近地层10、20和40m 高度处z/L随时间及平均风速的变化关系.可以看出,当平均风速较低时(10m 高度处约小于12m·s-1),z/L离散度较大,大部分时段其绝对值大于0.1;但当平均风速较大时,z/L随平均风速的变化较小,基本在区间[-0.1,0.1]内波动,此时大气层结近似趋于中性.
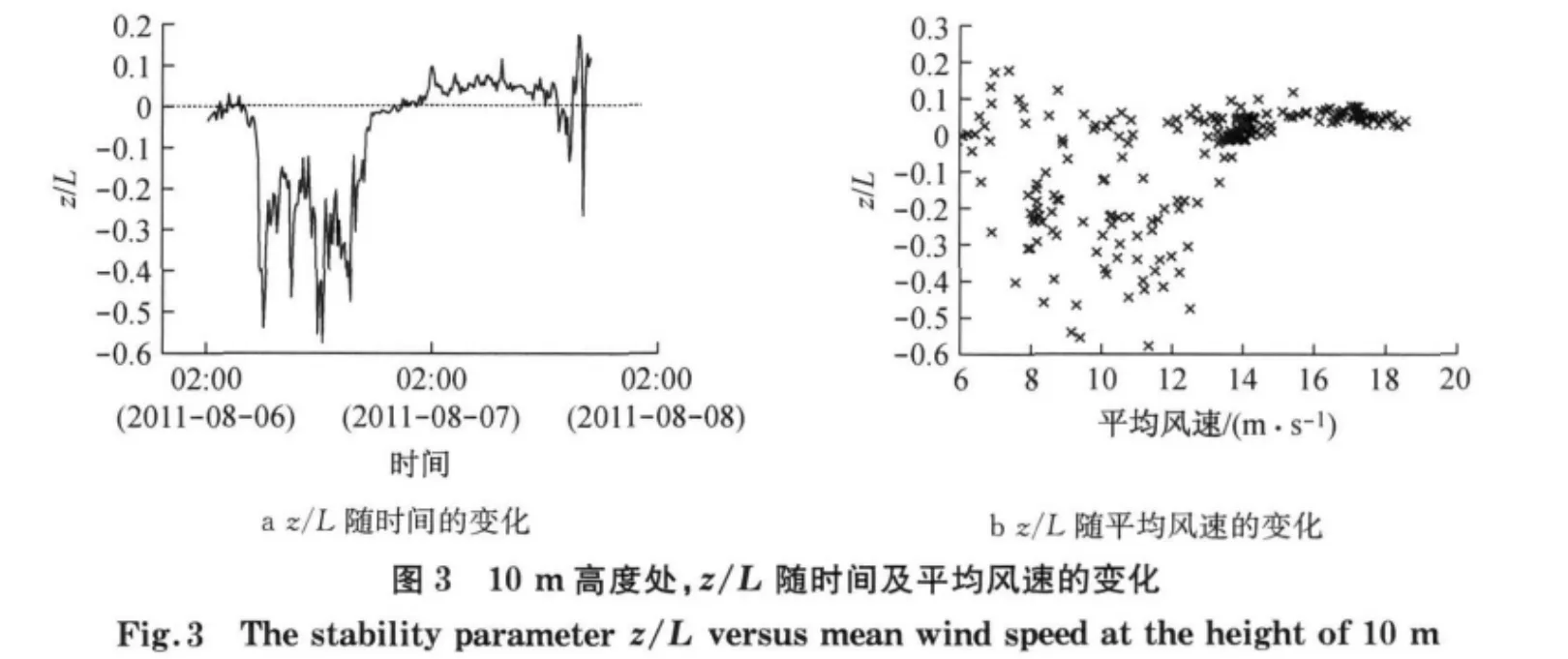

3.2 平均风剖面
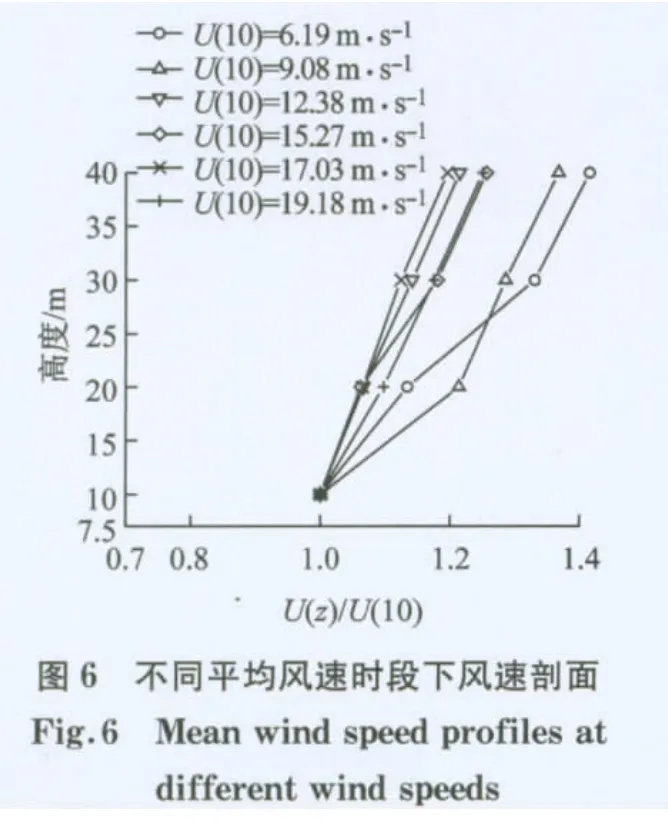
平均风速随高度的变化规律一直是结构风工程中重点关注的问题.图6给出了6组不同时段平均风速随高度的变化曲线,图中横坐标采用平均风速U(z)与U(10)的比值表示,U(10)为10m 高度处的平均风速.图中拟合对数律剖面和D-H 模型剖面时,摩擦速度是取各10 min时段样本的平均值,边界层高度zg采用了3.1.1节的计算值2 063 m.可以看出,10m 高度处平均风速小于12m·s-1的时段和平均风速大于12m·s-1的时段显现出明显不同的变化趋势,相同高度处前者远大于后者;而4组平均风速大于12m·s-1时段剖面曲线相差较小.由3.1.3节可知平均风速大小会影响大气稳定状态,而根据式(3)可知,大气稳定度又直接决定了平均风速随高度的变化形式,因而不同平均风速时段风速剖面形式会有所差别.分析表明,只有平均风速较大时段风速剖面才在理论上符合式(2)的对数率形式.
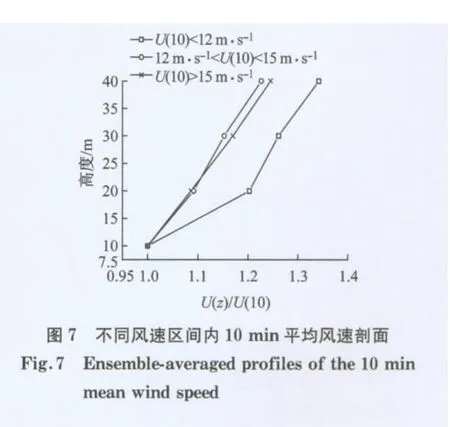
为做进一步分析,在图7 中还给出了不同平均风速区间内,各时段平均风速随高度变化的平均剖面曲线.图中显示,10m 高度处平均风速大于12m·s-1的两段风速区间内,平均风速剖面相差较小,但两者明显小于平均风速小于12m·s-1区间的实测结果.表明平均风速大于12m·s-1的时段的平均风速剖面曲线已趋于稳定,其结果可以用来表征该地区台风“梅花”影响下平均风速剖面特性.
为了将实测结果与经典风速剖面模型进行对比,在图8中给出了10m 高度处平均风速大于12m·s-1所有时段的平均剖面曲线、基于实测参数拟合的指数率模型、以及基于规范给定参数(粗糙度长度z0)的对数率模型和Deaves-Harris模型.从图中可见,基于实测参数拟合指数率模型、对数率模型和Deaves-Harris模型与实测结果均符合较好,与文献[15]中的结论有所不同.
3.3 湍流度剖面
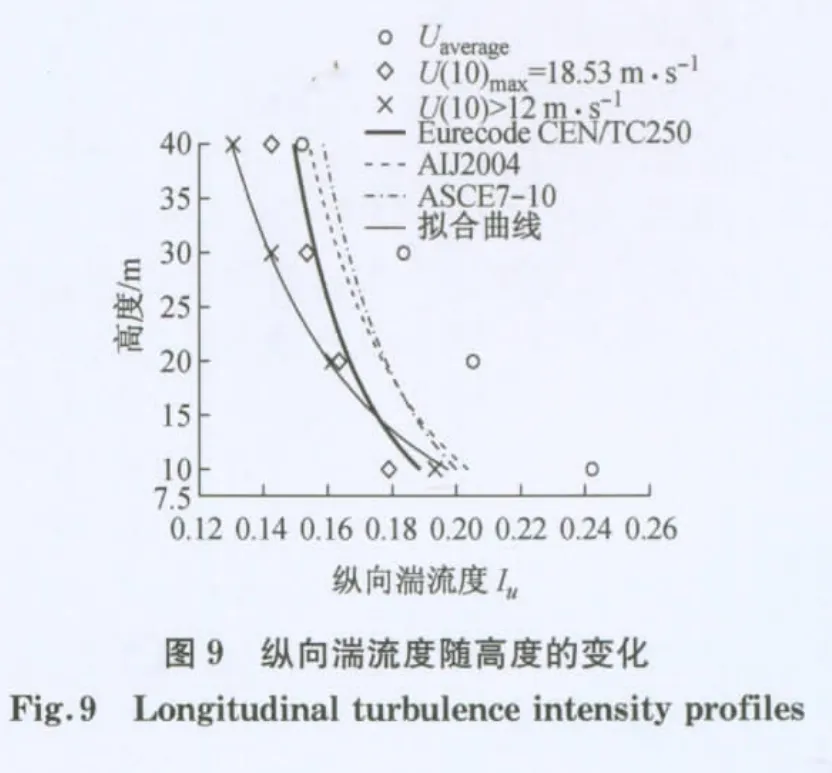
实测纵向湍流度Iu随高度的变化关系如图9所示,作为对比,图中还给出了一些国家规范[11,20-21]中规定的纵向湍流度剖面.由图可见,各高度处全部时段实测湍流度的平均值明显大于12m·s-1(10m处平均风速)以上风速时段的平均值以及最大风速时段的实测结果.由于风速较小时,大气层结偏离中性,因此12m·s-1以上风速时段纵向湍流度平均值更能代表台风“梅花”过程中中性大气层结状态下的湍流特性.通过与规范预测结果对比发现,10 m 高度处平均风速日本和美国规范预测结果略大于实测结果,但随着高度的增加两者的差距逐渐增大;而在10m 高度处,平均风速欧洲规范的预测结果小于实测结果,但在20、30和40 m 高度处结论相反,上述分析表明三种规范中的经验表达式均不能很好地反映实测纵向湍流度剖面特性.因此,参考ASCE7-10中纵向湍流度剖面的表达形式,基于各高度处实测数据对12m·s-1以上风速时段平均剖面进行了形如Iu=c(10/z)d的拟合,其中拟合参数c和d分别为0.20和0.30.

不同于纵向湍流度,各国规范并没有给出横向及竖向湍流度随高度变化的经验表达式,并且国内外的相关研究也相对缺乏.基于实测数据经计算分别得到了不同高度处横向和竖向湍流度实测结果,如图10—11所示.利用和纵向湍流度剖面相同的拟合表达式,通过拟合分别得到了12m·s-1以上风速时段横向和竖向湍流度剖面的经验表达式,横向湍流度剖面拟合参数c、d分别为0.14、0.23,竖向为0.097和0.23.
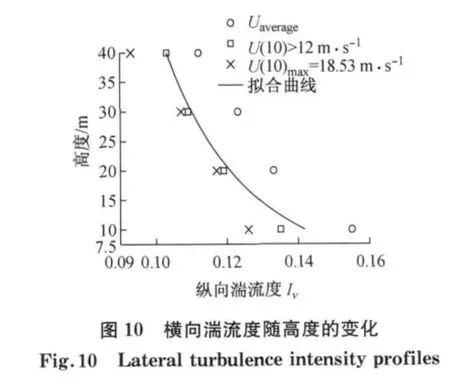
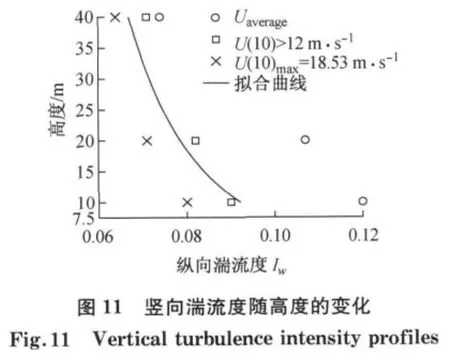
3.4 阵风因子剖面
阵风因子反映瞬时阵风的相对强度,是重要的风特性参数.与湍流度不同,各国规范中尚未给出阵风因子剖面的经验表达式.为直观掌握各向阵风因子随高度的变化规律,同时为工程设计提供参考,图12给出了各向实测阵风因子Gi随高度的变化关系,并对实测结果做了形如Gi=α(z/10)β的拟合,其中,α,β为待定参数.在图12中给出了相应的拟合公式.从图中可见,纵向和横向阵风因子(Gu和Gv)拟合结果与实测结果符合较好,而竖向阵风因子Gw拟合结果与实测结果符合稍差.但总体上看,拟合表达式还是可以很好地反映出各向阵风因子随高度的变化规律.
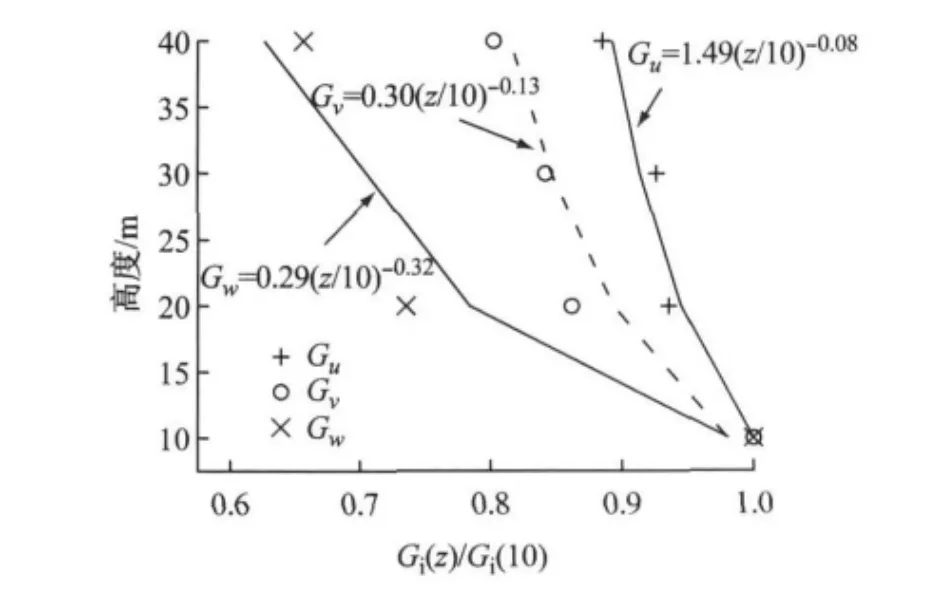
图12 阵风因子随高度的变化Fig.12 Gust factor profiles in longitudinal,lateral and vertical directions
4 结论
目前,基于台风数据的近地风剖面特性研究还相对欠缺,但这项工作对于结构风工程学科有着重要的意义.本文基于40m 测风塔上10、20、30和40 m 高度处风速仪记录的台风“梅花”实测数据,研究了平均风速、湍流度和阵风因子随高度的变化规律,得到了以下结论:
(1)利用公式计算得到的边界层高度随平均风速的增大而增大,实测平均值为2 063m,远远大于我国规范规定的B类地貌下的边界层高度(350m),但与文献[14]和文献[15]计算所得结果相近.
(2)当平均风速较大(10m 高度处约大于12m·s-1)时,大气稳定度参数z/L随平均风速的变化较小,基本在区间[-0.1,0.1]内波动.因此可以认为在风速较大时,大气层结近似趋于中性.
(3)指数率模型、对数率模型和Deaves-Harris模型都可以较好地描述整个台风“梅花”过程中浦东地区0~40m 高度近地层平均风速随高度的变化规律.
(4)将纵向湍流度剖面实测结果与美国、日本和欧洲规范中的经验结果进行了对比,发现三种规范中的经验表达式均不能很好的表达湍流度剖面的实测结果.本文参考ASCE7-10中纵向湍流度剖面的表达形式,得到了实测湍流度剖面的拟合表达式.另外,通过回归分析还得到了横向及竖向湍流度随高度变化的经验表达式,进一步丰富了我国风特性现场实测研究数据库.
(5)各国规范中尚未给出阵风因子剖面的经验表达式,本文对阵风因子剖面实测结果做了形如Gi=a(z/10)β的拟合,得到了相应的拟合公式,可以为今后工程设计提供参考.
[1] 戴益民,李秋胜,李正农.低矮房屋屋面风压特性的实测研究[J].土木工程学报,2008,41(6):9.DAI Yimin,LI Qiusheng,LI Zhengnong.Experimental study of wind pressures on a low-rise full-scale building[J].China Civil Engineering Journal,2008,41(6):9.
[2] 王旭,黄鹏,顾明.海边坡角可调试验房风荷载现场实测研究[J].振动与冲击,2012,31(5):176.WANG Xu,HUANG Peng,GU Ming.Field investigation on wind loads of a low building with adjustable roof pitch near sea[J].Journal of Vibration and Shock,2012,31(5):176.
[3] 庞加斌,林志兴,葛耀君.浦东地区近地强风特性观测研究[J]流体力学实验和测量,2002,16(3):33.PANG Jiabin,LIN Zhixing,GE Yaojun.Field measurements of strong wind characteristics near ground in Pudong district[J].Experiments and Measurements in Fluid Mechanics,2002,16(3):33.
[4] 顾明,匡军,全涌,等.上海环球金融中心大楼顶部风速实测数据分析[J].振动与冲击,2009,28(12):114.GU Ming,KUANG Jun,QUAN Yong,et al.Analysis of measured wind speed data on top of SWFC[J].Journal of Vibration and Shock,2009,28(12):114.
[5] 顾明,匡军,韦晓,等.上海环球金融中心大楼顶部良态风风速实测[J].同济大学学报:自然科学版,2011,39(11):1592.GU Ming,KUANG Jun,WEI Xiao,et al.Field measurement of strong wind speed of normal climate on top of Shanghai world financial center[J].Journal of Tongji University:Natural Science,2011,39(11):1592.
[6] 李秋胜,郅伦海,胡非.沙尘暴天气下城市中心边界层风剖面观测及分析[J].土木工程学报,2009,42(12):83.LI Qiusheng,ZHI Lunhai,HU Fei.Observation of wind profile and analysis of atmosphere boundary layer in urban areas[J].China Civil Engineering Journal,2009,42(12):83.
[7] 戴益民,李正农,李秋胜,等.低矮房屋的风载特性—近地风剖面变化规律的研究[J].土木工程学报,2009,42(3):42.DAI Yimin,LI Zhengnong,LI Qiusheng,et al.Wind loads on low-rise buildings:study on variation of near ground wind profiles[J].China Civil Engineering Journal,2009,42(3):42.
[8] 中华人民共和国建设部.GB5009—2001 建筑结构荷载规范[S].北京:中国建筑工业出版社,2002.Ministry of Construction of People’s Repubic of China.GB50009—2001 Load code for the design of building structures[S].Beijing:China Architecture and Building Press,2002.
[9] 王旭,黄鹏,顾明.基于台风“梅花”的近地层湍流积分尺度现场实测分析[J].同济大学学报:自然科学版,2012,40(10):1491.WANG Xu,HUANG Peng,GU Ming.Field measurements about integral scales of near-ground turbulence during Typhoon‘Muifa’[J].Journal of Tongji University:Natural Science,2012,40(10):1491.
[10] 王旭,黄鹏,顾明.上海地区近地台风实测分析[J].振动与冲击,2012,31(20):84.WANG Xu,HUANG Peng,GU Ming.Field measurement of typhoon characteristics near ground in Shanghai district[J].Journal of Vibration and Shock,2012,31(20):84.
[11] American Society of Civil Engineers.ASCE/SEI 7-10 Minimum design loads for buildings and other structures[S].New York:ASCE,2010.
[12] Simiu E,Scanlan R H. Wind effects on structures—fundamentals and applications to design[M].[S.l.]:John Wiley &Sons Inc.,1996.
[13] 尚伦宇,吕世华,张宇,等.青藏高原东部土壤冻融过程中近地层湍流统计特征分析[J].高原气象,2011,30(1):30.SHANG Lunyu,LÜ Shihua,ZHANG Yu,et al.Analysis on atmospheric surface layer turbulence characteristic during soil freezing and thawing seasons in Eastern Qinghai-Tibet plateau[J].Plateau Meteorology,2011,30(1):30.
[14] Tieleman H W.Strong wind observations in the atmospheric surface layer[J].Journal of Wind Engineering and Industrial Aerodynamics,2008,96:41.
[15] Li Q S,Zhi L H,Hu F.Field monitoring of boundary layer wind characteristics in urban area[J].Wind and Structures,2009,12:553.
[16] 郭凤霞,朱文越,饶瑞中.非均一地形近地层风速廓线特点及粗糙度的研究[J].气象,2010,36(6):90.GUO Fengxia,ZHU Wenyue,RAO Ruizhong.Study on the feature of surface layer wind velocity profile and the roughness over non-homogeneous landform[J].Meteorology Monthly,2010,36(6):90.
[17] Kaimal J C,Finnigan J J.Atmospheric boundary layer flows[M].New York:Oxford University Press,1994.
[18] Deaves D M.Harris R I.A mathematical model of the structure of strong winds[R].London:Construction Industry Research and Information Association,1978.
[19] Deaves D M.Computations of wind flow over changes in surface roughness[J].Journal of Wind Engineering and Industrial Aerodynamics,1981,7:65.
[20] Architectural Institute of Japan.AIJ 2004 recommendations for loads on buildings [S].Tokyo:Architectural Institute of Japan,2004.
[21] Technical Committee.CEN/TC250 Structural Eurocodes.Eurocode 1:actions on structures—general actions—part 1-4:wind actions [S].London:British Standards Institution,2004.
