基于地磁梯度的弹丸运动涡流磁场模型

向 超，卜雄洙，祁克玉

（1.南京理工大学机械工程学院，江苏 南京 210094；2.机电动态控制重点实验室，陕西 西安 710065）

0 引言

利用地磁场来进行导航和姿态测试的方法已经在航天、航海、机器人等领域有了长足的发展和运用［1－3］。目前所有利用地磁来进行弹体姿态测量和制导的方法都面临着背景磁场的干扰问题，载体上测得的地磁场强度的精度对于导航参数的计算影响很大，这导致地磁导航测姿技术目前还处于辅助的地位。背景磁场的复杂性使得载体背景磁场补偿成为制约弹上地磁场高精度测量的瓶颈。如何建立更高效、更精确的载体背景磁场补偿方法是当前急需解决的问题。

就利用地磁参数来测量弹丸姿态而言，背景磁场的本质就是除地磁场分量外的所有干扰磁场。传统的磁补偿方法从地磁传感器的零位误差、垂直误差、灵敏度误差入手，建立磁传感器的罗差补偿模型，先后出现了泊森（Poisson）公式补偿法、椭圆拟合补偿法、十二位置补偿法、最小二乘补偿法等［4］。这些方法只研究了静态情况下的载体固定磁场和感应磁场的影响，对动态下的涡流等的影响没有进行讨论，在一定程度上存在局限性，不能满足旋转弹丸高速飞行过程中的涡流干扰磁场的补偿要求。针对上述问题，本文提出了基于地磁梯度的弹丸运动涡流磁场模型。

1 弹丸涡流模型与地磁梯度

1.1 弹丸涡流磁场的数学模型

弹体的材料多为铁磁性物质，当弹体在地磁场空间中做俯仰、偏航和横滚运动时，弹体外壳形成闭合回路，根据法拉第电磁感应定律，弹体周围会产生涡流磁场。弹丸载体在地磁场空间中载体坐标系O－xbybzb的定义如图1所示。

图1 载体坐标系定义Fig.1 Definition of carrier coordinate system

上式中E为涡流磁场模型的涡流参数矩阵。涡流系数eij（i＝x，y，z；j＝x，y，z）只与弹体的材料特性、尺寸、磁传感器安装位置有关，只要这些参数确定，eij就是常数。从式（1）可以看出，弹丸的背景涡流磁场的大小跟载体坐标系三轴上地磁场分量的变化率有关。

1.2 地磁场梯度模型

地磁场模型是表示地磁场时空结构的函数表达式。人们常用球谐分析方法计算地磁场的全球模型，例如Taylor多项式模型、Legendre多项式模型、矩谐模型、冠谐模型和Spline函数模型［6］。根据地磁场模型的相关知识，可知地磁场矢量感应强度M在空间中随纬度方向和高度方向的距离变化而明显变化，经度方向的距离变化没有太大的影响，如图2所示。

图2 地磁场强度的梯度变化示意图Fig.2 Schematic diagram of gradient change of geomagnetic field

如图2所示建立弹体的相对高度－纬度坐标系，设弹丸发射点为A（M0）点，此处的地磁场强度大小为，在高度－纬度坐标系中为原点 （0，0）。弹丸在飞行过程中t时刻的高度－纬度坐标为 （xh，xL），在上述坐标系中为B（Mt）点，此时的地磁场强度大小为。设地磁场矢量强度的水平梯度为kL，高度梯度为kh，则t时刻弹丸所在空间地磁场强度可表示为：

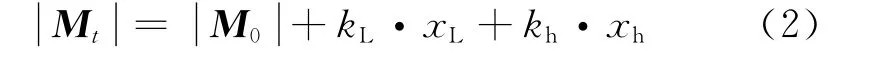
其中空间磁场比较均匀，则kL、kh为常数。

1.3 与飞机背景磁场的比较

文献［7］分析了地磁场梯度对飞机磁场求解精度的影响分析。但弹体涡流磁场与飞机涡流磁场相比存在明显不同：

1）飞机的磁背景建模是将地磁场和地磁场带来的一系列干扰磁场都视为背景磁场，它提高的是航空磁探测仪器的精度；弹丸的背景磁场补偿是针对除地磁场以外，弹丸动态飞行过程中的所有干扰磁场，提高的是弹载地磁场的测量精度。

2）弹丸的实际飞行轨迹和特点与飞机的飞行特点有较大差别，尤其在弹丸进行高速旋转的状态下，弹丸背景磁场中的涡流磁场比起飞机来说要复杂得多。

3）与飞机相比，弹丸的制作材料大多是钢，相对磁导率能达到1 000，而非铝合金之类相对磁导率较低的材料；同时用于磁性探测的飞机平均速度只有100～200m／s，而弹箭的飞行速度能达到飞机速度的5～6倍，运动过程中产生的涡流磁场是飞机的十倍甚至上百倍，对地磁场的测量精度影响较大。

4）飞机体积比较大，干扰磁场的补偿可以通过在适当位置安装传感器或补偿设备来实现，如远离飞机发动机和其他电子设备；弹丸体积有限，且传感器安装在指定的空间位置，因此不能采取飞机上的补偿方法。

因此需要根据弹丸涡流磁场特点，基于地磁场梯度模型对弹丸进行了优化研究。

2 考虑地磁场梯度的涡流优化模型

根据图1所示的载体坐标系和姿态矩阵变换理论［8］，Bbx、Bby、Bbz可用式（3）来表示。

其中

式（4）中ψ、θ、γ为载体的姿态角，I为地磁倾角。对式（4）等号两边同时求导，则地磁场M在载体坐标系三轴xb、yb、zb上的分量变化率、、可表示为：

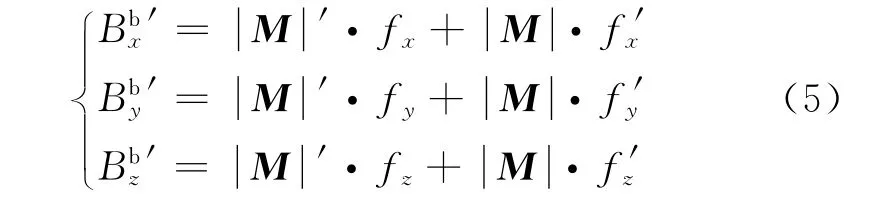
将式（5）代入涡流干扰背景场的数学模型式（1），有

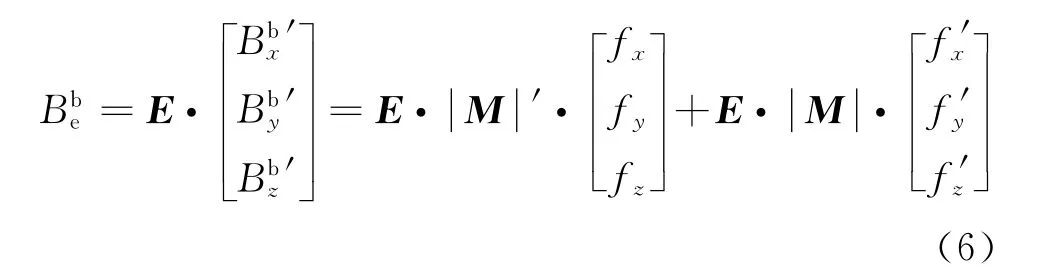
式（2）左右两边对时间t求导有

式（7）中VL为t时刻弹丸纬度方向速度；Vh为t时刻弹丸高度方向速度。将上式代入式（6），则有

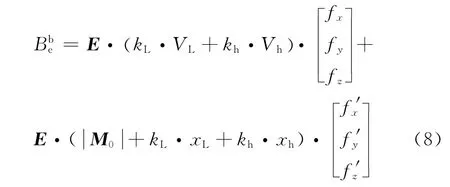
式（8）为考虑了地磁场梯度的影响后涡流磁场模型的完整表达式，其中、kL、kh为弹丸飞行区域的地磁场要素，可根据地磁场模型（IGRF等）得到；E为弹体的涡流系数矩阵，与弹体材料的电磁特性和尺寸结构有关，对于确定的弹丸是常系数矩阵；xL、xh为弹体飞行距离，与射程有关；VL、Vh、θ、ψ、γ为弹体实际飞行特征参数。从式（8）可以看出，在地磁要素不变的情况下，地磁梯度对涡流磁场的影响随着弹体线速度和姿态变化率的增大而增大；在飞行线速度和姿态相同的情况下，地磁梯度对涡流磁场的影响随着射程的增大而增加。

对于常规武器弹丸背景涡流磁场的研究，由于常规武器火炮弹丸的射程一般都在几十公里以内，弹丸飞行过程通常伴随较高的自转角速度［9］，如榴弹炮等。根据地磁场模型IGRF，在这个地域范围内，地磁场矢量的梯度很小，地磁场矢量强度变化率不超过10－5%。这种情况下认为飞行范围类地磁场矢量强度不变，即＝kL＝kh＝0，此时有＝E·［f′xf′yf′z］T。此时涡流背景磁场只与每个时刻弹丸的姿态角和角速度有关。对于战略战术导弹等大射程弹丸，其飞行过程跨越的地理区域比较大，一般可达几百到几千公里，此时地磁梯度的变化就比较明显，不能将 Mt′简单地忽略为零，必须按照式（8）来计算。由于此类弹丸的飞行特点是姿态比较稳定，不会出现很大的自转角速度，所以这种情况下的弹丸载体涡流干扰磁场主要是受地磁场梯度的影响。

3 误差分析与数值分析

3.1 地磁梯度对涡流磁场补偿精度和姿态角测量精度的影响

利用测量地磁场在弹体坐标系内三轴分量来解算姿态角时，涡流干扰背景磁场会引起传感器测量误差ΔB，进而照成姿态角的测量误差。在只考虑涡流磁场干扰的情况下，载体上磁传感器的检测到的周围磁场可表示为：

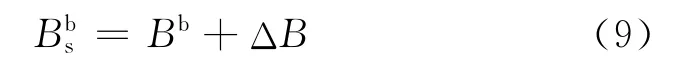
在利用磁传感器的输出进行姿态角的解算前，必须通过补偿，将中涡流干扰磁场去掉。定义涡流磁场的补偿效率为：

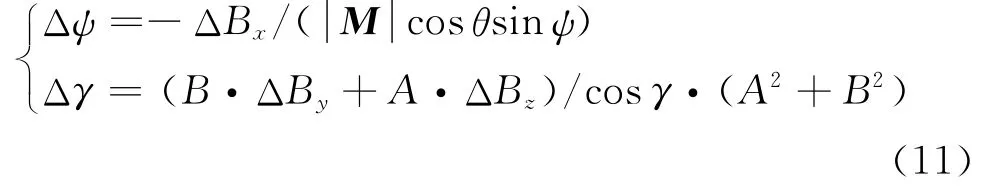
根据函数误差传递理论［9］和地磁测姿原理，当已知转动欧拉角θ时，其余两角ψ、γ的测量误差为

3.2 数值仿真分析

地球表面任一点的地球磁场参数都可由地磁场模型IGRF11计算得到［10］，利用IGRF11模型和MATLAB软件仿真分析地磁梯度对涡流磁场补偿精度和姿态角测量精度的影响。以射程在500km以内，弹道高度在1万m以下的弹体为例，如图3所示以南京地区东经119°、北纬32°为弹丸发射点O，以初始射角60°发射，20s到达高空1万m处的A点，之后经过300s平飞到达目标点D点，途经B、C两点。

图3 仿真弹道平面示意图Fig.3 Plan sketch of the simulation trajectory

在仿真中，弹丸滚转角速度为10r／s，偏航角30°不变，俯仰角OA段为60°，OE段保持0°不变。根据IGRF11地磁场模型，得到发射点O点处地磁矢量强度为49 549nT，计算得到 A、B、C、D四点处的地磁矢量强度水平梯度和垂直梯度如表1所示。

表1 测量点地磁场梯度Tab.1 Magnetic field gradient at measuring point

表2给出了利用MATLAB仿真的考虑地磁场梯度和不考虑地磁场梯度情况下的涡流磁场的补偿效率和经过涡流补偿后的姿态角结算误差。姿态角解算是利用已知的俯仰角θ和磁传感器输出来计算其余两角ψ、γ。

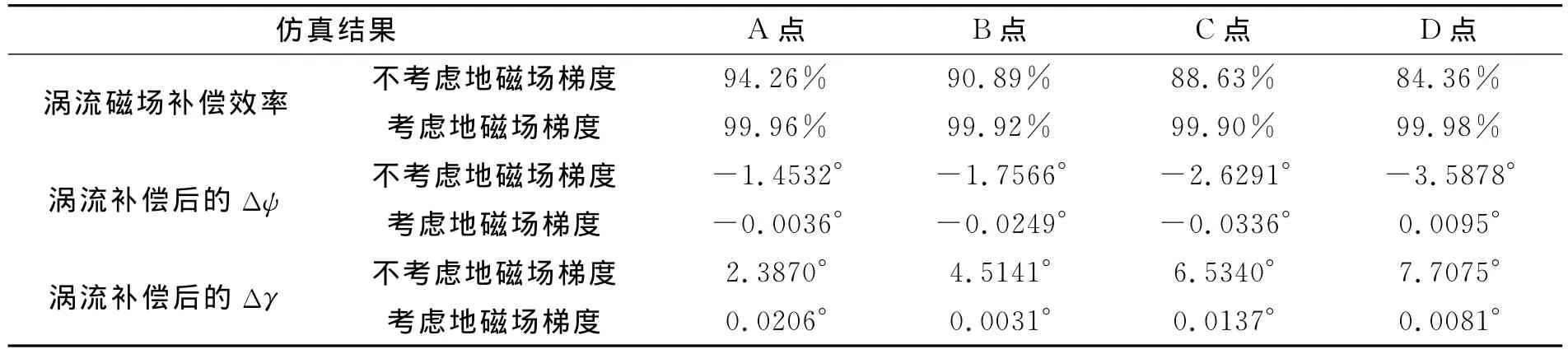
表2 数值仿真结果Tab.2 Magnetic field gradient at measuring point

从表2可以看出考虑地磁场梯度以后的涡流补偿效率和姿态角解算精度明显高于不考虑地磁场梯度时的结果。在同样的仿真条件下（线速度和姿态变化率相同），随着弹丸跨越地域范围的增加（飞行纬度和高度的增加），地磁场梯度对涡流磁场的影响也会增大，涡流补偿效率和姿态角精度会降低。当弹丸飞行跨度达到几千公里时，地磁场梯度的影响将会导致地磁定姿方法的可靠性大大降低。在工程运用中，需要根据实际情况，利用地磁场梯度模型和优化的涡流磁场模型提高地磁定姿的可靠性。

4 结论

本文提出了考虑地磁场梯度下的弹体运动涡流磁场模型。该优化模型结合弹体涡流磁场与地磁梯度的特点，阐明了运动涡流磁场与弹体飞行参数、地磁场矢量强度和地磁梯度之间的数学关系，完整地体现了影响弹体涡流磁场的因素。数值仿真实验的结果表明，不考虑地磁场梯度会造成涡流补偿效率和姿态角解算精度的降低，且随着弹体飞行跨越地理范围的增大，其误差也增大。本文提出的模型有效可靠，可用于弹体背景磁场的补偿研究。实际工程运用中，需根据具体情况，利用优化的涡流磁场梯度模型来提高地磁定姿的可靠性。

［1］Mahony R，Hamel T，Pflimlin J M.Nonlinear complementary filters on the special orthogonal group［J］.IEEE Trans，Autom.Control，2008，53（2）：1 203－1 218.

［2］Zhu R，Zhou Z.A small low－cost hybrid orientation system and its error analysis［J］.IEEE Sensors Journal，2009，9（3）：223－230.

［3］Wang F，Jin H.Design a mini－type marine attitude measurement system for self－propelled model trials ［J］.Measurement，2009，42（6）：954－962.

［4］Takaya Inamori，Nobutada Sako，Shinichi Nakasuka.Magnetic dipole moment estimation and compensation for an accurate attitude control in nano－satellite missions［J］.Acta Astronautica，2011，68（11－12）：2 038－2 046.

［5］向超，卜雄洙.高旋弹丸背景涡流磁场建模与仿真［J］.哈尔滨工程大学学报，2012.XIANG Chao，BU Xiongzhu.Modeling and simulation of the background eddy current magnetic field of high spinning projectile［J］.Journal of Harbin Engineering University，2012.

［6］李玎.基于磁传感器组合的旋转弹体姿态测试方法研究［D］.南京：南京理工大学，2009.

［7］谭斌，林春生，张宁，等.地磁场梯度对飞机磁场求解精度的影响分析［J］.武汉大学学报信息科学版，2011，36（12）：1 482－1 485.TAN Bin，LIN Chunsheng，ZHANG Ning，et al.Impacts of geomagnetic gradient on solving precision of aircraft magnetic field［J］.Geomatics and Information Science of Wuhan University，2011，36（12）：1 482－1 485.

［8］向超，卜雄洙，李玎.基于三正交磁传感器的新型旋转弹体定姿方法［J］.中国惯性技术学报，2011，19（4）：443－447.XIANG Chao，BU Xiongzhu，LI Ding.New spinning projectile's attitude measurement based on three pair－wiseorthogonal magnetic sensors［J］.Journal of Chinese Inertial Technology，2011，19（4）：443－447.

［9］韩子鹏.弹箭外弹道学［M］.北京：北京理工大学出版社，2008.

［10］Zhao Wenyan，Wang Gang，Guo Liangtian.The HF channel EM parameters estimation under a complex environment using the modified IRI and IGRF model［J］.Antennas and Propagation，2011，59（5）：1 778－1 783.