克莱姆法则的推广和完善

钱志祥

(肇庆科技职业技术学院 基础教学部，广东 肇庆 526020)

克莱姆法则的推广和完善

钱志祥

(肇庆科技职业技术学院 基础教学部，广东 肇庆 526020)

克莱姆法则是线性代数中的重要内容，但克莱姆法则只解决了当线性方程组系数行列式不等于零时，线性方程组的解的存在性和唯一性问题.当系数行列式等于零时，线性方程组无解或者有无穷多解.什么条件下线性方程组无解？什么条件下线性方程组有无穷解？当线性方程组有无穷解时，这无穷解的通解的结构是什么？克莱姆法则没有给出答案.所以需要推广和完善，这在线性方程组的解的结构理论上是很有用的.

克莱姆法则；系数矩阵；系数行列式

0 引言

克莱姆法则完美地解决了含有n个未知量n个方程的线性方程组在其系数行列式不为零时，其解的存在性、个数及求解(公式)问题.[1-4]但是当其系数行列式等于零时，其解的情况没有解决，这时线性方程组无解或者有无穷多解，那么在什么情况下线性方程组无解，在什么情况下线性方程组有无穷多解，有无穷多解时通解的结构又是什么？本文将给予推广和完善，使克莱姆法则更加完美，具有更强的理论价值.

1 主要结论

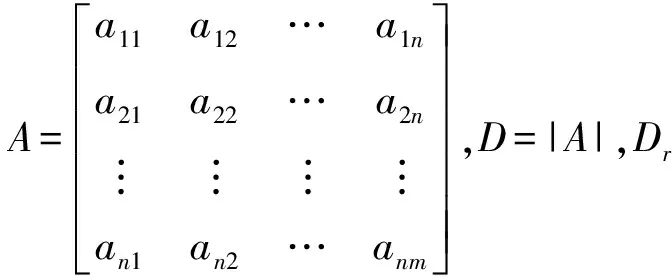
定理1 设线性方程组

(1)

的系数矩阵为

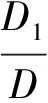
(Ⅱ)当系数行列式D=0时，且Dj(j=1,2,…,n)不全为零时，方程组无解;

(Ⅲ)当系数行列式D=0时，且Dj(j=1,2,…,n)全为零时，方程组有无穷多解，其通解的结构为：

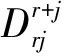
证明：(Ⅰ)当n=1时，结论是明显的.设ngt;1,令j是整数1,2,…,n中的任意一个，分别以Aij,A2j,…,Anj乘方程组(1)的第一，第二，直至第N个方程后相加得：

(a11A1j+a21A2j+…+an1Anj)x1+…+(a1jA1j+a2jA2j+…+anjAnj)xj+…+(a1nA1j+a2nA2j+…+annAnj)xn=b1A1j+b2A2j+…+bnAnj，

易知,xj的系数等于D，而xj(i≠u)的系数都是零；因此等式左端等于Dxj，而等式右端刚好是行列式

这样得到：Dxj=Dj.令j=1,2,…,n，得到方程组

(2)

先证方程组(1)的每一解都是方程组(2)的解.事实上,设∂1,∂2,…,∂n是方程组(1)的一个解.则在(1)中把xi代以∂i(i=1,2,…,n)就得到一组等式.对于这一组等式施以方程组(1)到方程组(2)的变换，得到下面的一组等式：D∂1=D1,D∂2=D2,…,D∂n=Dn.即是说，∂1,∂2,…,∂n也是方程组(1)的一个解.

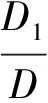
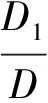
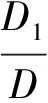
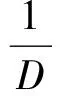
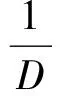
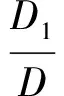
(Ⅱ)由方程组(2)知：当系数行列式D=0且Dj(j=1,2,…,n)不全为零时，方程组(2)N个方程中至少有一个没有解，所以方程组(1)无解.

(Ⅲ)当系数行列式D=0且Dj(j=1,2,…,n)全为零时，方程组(2)N个方程均有无穷解，所以方程组(2)有无穷多解，从而方程组(1)有无穷多解.这时不妨设Dr位于D的左上角，Dr为D的一个最高非零的r阶子式.这时方程组(1)显然与下列方程组同解.

(3)

因为rlt;n，将方程组(3)改写为：

(4)

方程组(4)作为x1,x2,…,xr的一个方程组，它的系数行列式Dr≠0，由证明(Ⅰ)知对于xr+1,xr+2,…,xn的任意一组值，方程组(4)，也就是方程(1)，都有唯一的解，xr+1,xr+2,…,xn就是方程组(1)的一组自由未知量，由证明(Ⅰ)可以解出x1,x2,…,xr：

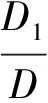
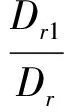
同理可得：

…

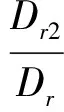
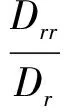
即方程组(1)的通解为

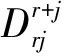
[1] 北京大学数学系几何与代数教研室代数小组.高等代数：第2版[M].北京：高等教育出版社，1988:83-84.

[2] 张禾瑞，郝鈵新.高等代数：第4版[M].北京：高等教育出版社，1999：136-138.

[3] 杨子胥. Cramer法则的推广[J].数学通报，1983(4):29-30.

[4] 赵振华.广义行列式与Cramer法则[J].数学通报,1993(9):41-43.

[5] 王萼芳,石生明.高等代数:第3版[M].北京：高等教育出版社，2003：136-138.

[责任编辑邓杰]

TheExtensionandRefinementofCramerRule

QIAN Zhi-xiang

(Basic Education Department of Zhaoqing Polytechnic Technology College, Zhaoqing Guangdong 526020, China)

Cramer rule is an important content in linear algebra. But Cramer rule only solved the linear system of equations determinant of coefficient is not equal to zero, the system of linear equations solution existence and uniqueness problem. When the determinant of coefficient is equal to zero, system of linear equations has no solution or has an infinite number of solutions. What conditions linear equations has no solution? What conditions linear equations with infinite solutions? When solutions of linear equations with infinite time, what is the structure of general solutions of infinite solutions? Cramer did not give an answer. So it needs to promote and perfect, and it is very useful in the system of linear equations solution structure theory.

Cramer rule; coefficient matrix;determinant of the coefficients

2012-12-16

钱志祥(1974—),男,安徽巢湖人.讲师，硕士，主要从事微分算子研究.

O13

A

1674-5248(2013)02-0031-03