M-矩阵Hadamard积最小特征值下界的估计

2013-11-30杨晓英

四川文理学院学报 2013年2期

关键词：下界对角特征值

刘新，杨晓英

(四川信息职业技术学院基础教育部，四川广元 628017)

M-矩阵Hadamard积最小特征值下界的估计

刘新，杨晓英

(四川信息职业技术学院基础教育部，四川广元 628017)

M-矩阵；Hadamard积；最小特征值；下界

0 引言

为表述方便，我们首先给出一些概念.记Rm×n(Cm×n)表示m×n阶实(复)矩阵集合；N表示正整数集合；ρ(P)表示n×n阶非负矩阵P的Perron根.

定义1[1]276-278设A=(aij)∈Rn×m,且aij≤0,i≠j,则称矩阵A为Z矩阵(简记为A∈Zn×n).

定义2[1]296设A=(aij)∈Zn×n，则A可以表示为A=λI-B，其中B≥0, 当λ≥ρ(B)时，则称A为M-矩阵.特别地，当λgt;ρ(B)时，称A为非奇异M-矩阵；当λ=ρ(B)时，称A为奇异M-矩阵.

同时，记τ(A)=min{|λ|:λ∈σ(A)}, (其中σ(A)表示矩阵A的谱),τ(A)称为A的最小特征值.

Yong，[3-4]Song，[5]Chen[6]分别证明了上述猜想的正确性.

Li Hou-biao等在文献[7]给出了下面的下界估计式：

1 符号与引理

首先，我们给出一些记号,它们会在后面的讨论中用到.记:

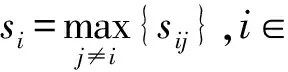
引理1[7]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,A-1=(bij). 则

引理2[8]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,A-1=(bij).则

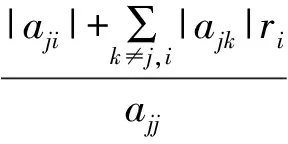
引理3[10]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,A-1=(bij) . 则

引理4[8]设A=(aij)∈Rn×n是M-矩阵,A-1=(bij)是双随机矩阵. 则

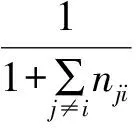
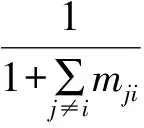
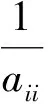
引理6[4]设A-1是双随机矩阵, 则Ae=e,ATe=e, 其中e=(1,1,…,1)T.

引理7[11]设A=(aij)n×n是任意复矩阵,xi,x2,…,xn是正实数.则A的所有特征值都位于复平面的下列区域之中

2 主要结果

定理1 设A=(aij)∈Rn×n是不可约M-矩阵，A-1=(bij)是双随机矩阵.则

证明：由文献[10]中定理2.1的证明，可知

0lt;nj≤1,j∈N.

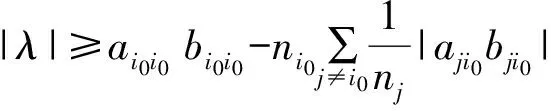
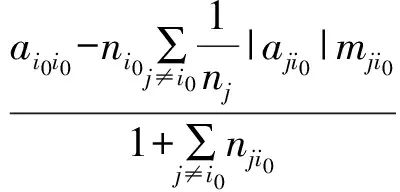
若A是可约的.不失一般性，假设A是具有不可约对角块Aii(i=1,2,…,k)的块上三角矩阵，则A-1仍是块上三角矩阵，且

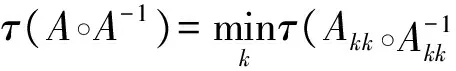
结论仍然成立.

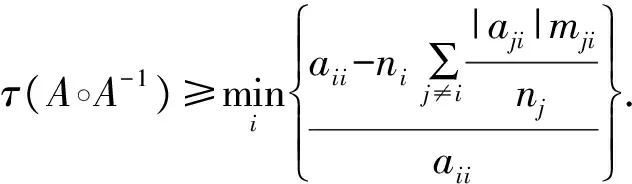
应用引理4和引理7，类似定理1的证明可得如下定理，其证明过程不再赘述.

定理2 设A=(aij)∈Rn×n是不可约M-矩阵,A-1=(bij) 是双随机矩阵.则

3 例子

例3.1[7]设

易知A是M-矩阵, 通过Matlab计算得

因此,A-1是双随机矩阵, 且

依据Fiedler和Markham的猜想:

依据文献[7]中定理3.1的结论, 得:

依据文献[8]中定理3.2的结论, 得:

由本文定理1得:

由本文定理2得:

由例3.1的数值结果知, 定理1和定理2有效地改进了Fiedler和Markham的猜想和文献[7-8]中相应的结果.

例3.2 设

易知A是非奇异M-矩阵, 且

依据Fiedler和Markham的猜想:

依据文献[8]中定理3.4的结论, 得:

由本文推论1得:

由例3.2的数值结果知, 推论1也很好地改进了Fiedler和Markham的猜想和文献[8]中定理3.4的结果.

[1] 陈景良, 陈向晖. 特殊矩阵[M].北京:清华大学出版社,2000.

[2] Fiedler M, Markham T.AnInequalityfortheHadamardProductofanM-matrixandInverseM-matrix[J].Linear Algebra Appl,1988(101):1-8.

[3] Yong Xue-rong.ProofofaConjectureofFiedlerandMarkham[J].Linear Algebra Appl,2000(320):167-171.

[4] Yong Xue-rong, Wang Zheng.OnaconjectureofFiedlerandMarkham[J].Linear Algebra Appl,1999(288): 259-267.

[5] Song Yong-zhong.OnanInequalityfortheHadamardProductofanM-matrixanditsInverse[J].Linear Algebra Appl, 2000( 305):99-105.

[6] Chen Shen-can.ALowerBoundfortheMinimumEigenvalueoftheHadamardProductofMatrices[J].Linear Algebra Appl, 2004(378):159-166.

[7] Li Hou-biao, Huang Ting-zhu, Shen Shu-qian, et al.LowerBoundsfortheMinimumEigenvalueofHadamardProductofanM-matrixanditsInverse[J].Linear Algebra Appl,2007(420):235-247.

[8] Li Yao-tang, Chen Fu-bin, Wang De-feng.NewLowerBoundsonEigenvalueoftheHadamardProductofanM-matrixanditsInverse[J].Linear Algebra Appl,2009(430):1423-1431.

[9] Li Yao-tang, Liu Xin, Yang Xiao-ying, et al.SomeNewLowerBoundsfortheMinimumEigenvalueoftheHadamardProductofanM-matrixanditsInverse[J].Electronic Journal of Linear Algebra,2011(22):630-643.

[10]Li Yao-tang, Li Yan-yan, Wang Rui-wu, et al.SomeNewBoundsonEigenvaluesoftheHadamardProductandtheFanProductofMatrices[J].Linear Algebra Appl,2010(432):536-545.

[11]Vargar S.MinimalGerschgorinsets[J].Pacific J Math,1965(2):719-729.

[责任编辑邓杰]

NewLowerBoundsontheMinimumEigenValuefortheHadamardProductofM-matrices

LIU Xin, YANG Xiao-ying

(Basic Education Ministry of Sichuan Information Technology College, Guangyuan Sichuan 628017, China)