基于流量预估的直拉式冷轧机液压张力控制策略

张浩宇，孙 杰，张殿华，曹剑钊

(东北大学 轧制技术及连轧自动化国家重点实验室，沈阳 110004)

随着工业的发展，市场对钢的性能的要求越来越高［1，2］.通过冷轧实验，冷轧带钢性能的优化以及开发新钢种成为钢铁业的一个重要需求.传统卷取式可逆轧机由于其自身设备原因，不适合做改进钢的性能以及钢种开发的试验研究.直拉式冷轧实验轧机适合对单片短轧件进行实验，适合钢的品种开发和冷轧工艺的研究与优化［3～6］.

直拉式冷轧实验轧机的设备示意图如图1所示.该轧机的特点是:在轧机两侧设置张力液压缸，通过张力液压缸尾端的液压夹头夹持带钢两端以产生和保持张力［7］.张力液压缸无杆腔接入恒压油源，通过性能优异的伺服阀控制有杆腔的流量，继而驱动液压缸产生并保持张力.张力液压缸配备有高精度高响应的位置传感器，用于反馈其实际位置以及计算其移动速度.在张力液压缸的有杆腔和无杆腔均配置了高精度的油压传感器，用于计算液压缸产生的张力.

然而，在动态下，单纯设置张力控制器对实际张力进行闭环控制的方式，其控制信号只与实际张力偏差相关，并未考虑张力液压缸在运动过程中所需的大量进出流量.其无法满足张力液压缸速度与轧制速度匹配且同时维持张力稳定的控制要求.本文开发了基于流量预估控制的张力控制策略，并应用于现场实际，获得了高精度的张力控制效果.

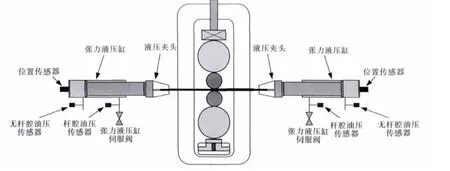
图1 直拉式冷轧机设备示意图Fig.1 Schematic diagram of equipment of hydraulic－tension experimental cold mill

1 液压张力控制策略

直拉式冷轧实验机的张力控制系统如图2所示.为了实现在无负载的情况下张力液压缸的移动，系统设置了位置控制器，该控制器基于张力液压缸实际位置与设定位置之间的偏差，输出相应的伺服阀控制信号，控制有杆腔进出油的流量，实现张力液压缸位置的控制.在轧制开始时，系统需通过张力控制器建立静态张力，该控制器基于实际张力与设定张力之间的偏差，输出相应的伺服阀控制信号，实现对静态张力的闭环控制.由于不同压力下伺服阀的零偏有差异，该控制器设置有积分环节，以补偿零偏造成的张力控制偏差.当静张建立后，待液压缸开始运动时，将锁定静张控制器的输出，以保持该静态张力.该控制器在张力液压缸静态下能满足较高的张力控制精度.当轧制开始后，张力液压缸需在与轧制速度相协调的前提下，保持张力的稳定.这时，张力液压缸在移动过程中液压油的进出流量较大，只与张力偏差相关的控制信号很难实现张力的稳定控制.于是设置了流量预估控制与动态张力补偿控制相结合的液压张力控制策略，用以实现动态下的高精度液压张力控制.

图2 液压张力控制系统框图Fig.2 Diagram of hydraulic tension control system

流量预估控制以伺服阀流量公式为基础，通过张力前馈控制环节预估匹配预估压力所需的流量，通过速度前馈控制环节预估匹配轧制速度所需的流量，并通过控制因子修正环节补偿因参数变化对预估控制精度造成的影响，最终输出为流量预估控制信号.动态张力补偿控制用于补偿流量预估控制后剩余的张力偏差，并根据实际轧制速度的变化，设置了相应的变增益控制环节，最终输出为动态张力补偿控制信号.流量预估控制信号与动态张力补偿控制信号相加后，叠加在锁定的静张控制器控制量上，作为最终伺服阀的控制信号.

2 流量预估控制

用于张力控制的液压伺服系统如图3所示.系统由一个压力为Ps的恒压源供油，其中回油压力为P0;张力液压缸的有杆腔与伺服阀阀口A相连，有杆腔压力为Prod;无杆腔采用恒压力控制，其压力为Ppis.伺服阀根据给定的控制电流的极性及大小，控制阀口A进出油，以实现对张力液压缸的控制.当给定控制电流使阀芯有一个正向位移时，在压力差 Ps－Prod的作用下，阀口 A进油，液压缸活塞杆缩回.若阀芯有一个反向位移时，在压差Prod－P0(一般认为回油压力P0≈0，则此时压差为Prod)的作用下，有杆腔泄油，液压缸活塞杆伸出.

图3 张力控制的液压伺服系统示意图Fig.3 Schematic diagram of hydraulic servo system for tension control

根据伺服阀流量公式［8，9］，在有杆腔进出油时阀口的流量如式(1)和式(2)所示:

式中，Cd为伺服阀流量系数;ρ为油液的密度，kg/m3;Ain为进油时的阀口面积，m2;Aout为出油时的阀口面积，m2.

其中，阀口的面积决定于阀芯的位移，所以其直接取决于控制电流，如式(3)和式(4)所示:

式中，Iin为阀口A进油时伺服阀控制电流，%;Iout为阀口A出油时伺服阀控制电流，%.

根据活塞力平衡方程，可得设定张力与预估有杆腔压力之间的关系如式(5)所示:

其中无杆腔压力采用恒压力控制，即Ppis为常数，则设定张力只与无杆腔压力呈线性关系，如式(6)所示:

式(5)与式(6)中，Fref为设定张力，kN;Prod，ref为基于设定张力的预估有杆腔压力，MPa;Arod为有杆腔有效面积，m2;Apis为无杆腔有效面积，m2;ktp为张力与压力传递因子，kN.

在张力前馈控制环节，张力液压缸依据轧制方向运动.相对于式(6)中在设定张力下的预估压力，入口侧液压缸流量如式(7)所示，出口侧液压缸流量如式(8)所示:

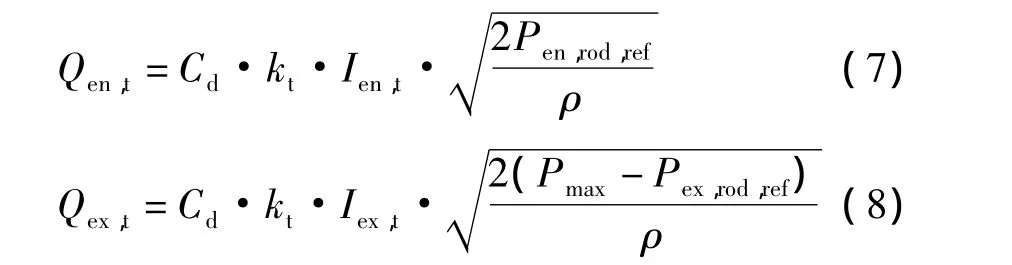
式中，Qen，t为入口侧张力液压缸预估压力匹配流量，m3/s;Qex，t为出口侧张力液压缸预估压力匹配流量，m3/s;Pen，rod，ref为入口侧预估有杆腔压力，MPa;Pex，rod，ref为出口侧预估有杆腔压力，MPa;Pmax为系统最大压力(对应可产生最大张力)，MPa;kt为张力前馈控制传递因子，m2;Ien，t为入口侧伺服阀控制电流，%;Iex，t为出口侧伺服阀控制电流，%.

在速度前馈控制环节，入出口侧张力液压缸的速度需要与主机的速度相协调，该速度可通过轧制速度结合带钢前后滑系数得到.由于张力液压缸的速度与流量呈线性关系，可得入出口侧的张力液压缸速度与有杆腔流量关系式如式(9)和式(10)所示:

式中，Qen，s为 Qex，s入口侧张力液压缸速度匹配流量，m3/s;Qex，s为出口侧张力液压缸速度匹配流量，m3/s;Cs为速度前馈流量系数;b为带钢后滑率;f为带钢前滑率;Vr为轧辊线速度，m/s.

为了在保证张力液压缸速度与轧制速度相匹配的情况下，依据设定张力对实际张力进行稳定控制.于是，在流量满足张力匹配与速度匹配时，取得流量预估控制的伺服阀控制信号如式(11)和式(12)所示:

式中，Ien为入口侧张力液压缸流量预估控制量，%;Iex为出口侧张力液压缸流量预估控制量，%;αen为入口侧流量预估控制因子;αex为出口侧流量预估控制因子;Fen，ref为入口侧设定张力，kN;Fex，ref为出口侧设定张力，kN.

在轧制过程中，一些重要参数的变化(如前后滑、油温等)会对流量预估的控制精度造成影响.因此，系统引入了控制因子修正环节.该环节在轧制过程中不断地根据实测变量对流量预估控制因子进行修正，以补偿在参数变化下的流量预估控制的精度.

流量预估的控制结果与实际张力可能存在一定差异，应用实测带钢速度、实测轧制速度以及伺服阀控制电流反馈值推算当前流量预估控制产生的张力.继而得出修正控制因子，如式(13)和式(14)所示:

式中，αen*为入口侧根据实测值推算的修正控制因子;αex*为出口侧根据实测值推算的修正控制因子;Fen，act为入口侧实际张力，kN;Fex，act为出口侧实际张力，kN;Ven，act为入口侧带钢实际速度，m/s;Vex，act为出口侧带钢实际速度，m/s;Ien，act为入口侧张力液压缸伺服阀反馈实际控制电流，%;Iex，act为出口侧张力液压缸伺服阀反馈实际控制电流，%.

基于指数平滑法，得出修正后的流量预估控制因子，如式(15)和式(16)所示:

式中，αen，cor为入口侧修正后的流量预估控制因子;αex，act为出口侧修正后的流量预估控制因子;αen，act为入口侧修正前使用的控制因子;αex，act为出口侧修正前使用的控制因子;αcor为修正速度因子，其取值范围为0≤αcor≤1，反映了该修正环节对流量预估控制的补偿作用大小.

3 动态张力补偿控制

为了获得高精度且无静差的张力控制效果，系统设置了动态张力补偿控制环节.该环节主要完成张力液压缸动态中对流量预估控制无法消除的张力偏差进行补偿.其采用积分控制器，将实际张力偏差作为反馈信号，最终输出为伺服阀的动态张力补偿控制量.

在轧制过程中，张力液压缸移动速度的变化直接影响到张力液压缸有杆腔内用于维持张力设定值的油量.于是，系统设置了与张力液压缸速度相关的变增益积分系数，用以补偿速度变化对张力补偿效果的影响，如式(17)所示:

式中，Gdtc为动态张力补偿控制器变增益系数;tres，int为积分控制器积分时间，s;lres，int为积分控制器跟踪距离，m;Vtc为张力液压缸实际速度，m/s.

4 实际应用

该策略已经成功应用于某直拉式冷轧实验机.其设备参数如表1所示.

表1 轧机主要参数Table 1 Major parameters of the mill

其自动化系统采用两级控制，网络配置图如图4所示.

过程控制系统主要完成模型设定以及数据记录和管理等功能.模型设定功能包括完成轧制规程计算、轧制策略和负荷分配计算、轧制规程极限值检查与修正.数据记录和管理功能中，包括实际数据记录，即PDI数据，如钢种、成分、原料厚度、成品厚度、宽度和长度等;轧制过程工艺数据，如设定厚度、实际厚度、设定辊缝、实际辊缝、设定轧制力、实际轧制力等.人机界面系统主要完成轧制过程监视、故障诊断、报警信息管理以及设定与实际数据显示等功能.

基础自动化控制系统分为两部分，即轧机主控系统和辅助控制系统.轧机主控系统采用S7－400+FM458的基本结构.S7－400主要完成主令速度控制、电动压下和轧机标定、轧机刚度测试以及其他辅助逻辑控制，FM458主要完成液压辊缝控制和张力自动控制.辅助控制系统采用S7－300 PLC，主要完成对液压站、设备及工艺润滑站的启停控制.轧机主传动采用 SIEMENS的6RA70直流调速器，电动压下交流传动采用SIEMENS 6SE70交流变频器.

图4 直拉式冷轧实验机计算机控制系统配置图Fig.4 Network configuration of hydraulic－tension experimental cold mill

在某一轧制道次，入口设定张力为37.4 kN，出口设定张力为35.3 kN.在轧机升速至速度为0.38 m/s的过程中，入出口侧流量预估控制曲线如图5所示.

由图5可知，随着速度的增大，入口侧流量预估控制给定负控制量且逐渐增加，实现入口侧张力液压缸沿轧制方向的移动，其中控制量的变化趋势与速度增大趋势一致;出口侧流量预估控制给定正控制量且逐渐增大，实现出口侧张力液压缸沿轧制方向的移动，其中控制量变化趋势与速度变化趋势一致.

图6给出了在图5控制量作用下实际张力的控制效果.入口张力误差在±0.8 kN之内，出口张力误差在±1 kN之内.该控制策略的张力控制误差均在±3%之内.

图5 流量预估控制量曲线Fig.5 Curves of flow prediction control values

图6 张力控制效果Fig.6 Control results of tension

5 结论

(1)建立了直拉式冷轧实验机的液压张力策略，通过设置流量预估控制实现了张力液压缸动态下流量的速度匹配与张力匹配.

(2)推导出了实现速度匹配和张力匹配的流量预估控制信号，实现了对流量预估控制因子的在线修正.预估控制剩余的张力偏差得到了动态补偿.

(3)该策略控制效果良好，为钢的品种开发和冷轧工艺的研究与优化提供了保障.

［1］ S C Paolinelli，M A da Cunda.Development of a new generation of high permeability non－oriented silicon steels［J］.Journal of Magnetism and Magnetic Materials，2006，304:e596－e598.

［2］ S A Abdul Azis，I Jauhari，N W Ahamad.Improving surface properties and wear behaviors of duplex stainless steel via pressure carburizing ［J］.Surface ＆ Coatings Technology，2012，210:142－150.

［3］ H R Koofigar，F Sheikholeslam，S Hosseinnia.Unified gauge－tension control in cold rolling mills:A Robust Regulation Technique［J］.International Journal of Precision Engineering and Manufacturing，2011，12(3):393－403.

［4］ J S Gunasekera，Jia Zhengjie，J C Malas，et al.Development of a neural network model for a cold rolling process ［J］.Engineering Applications of Artificial Intelligence，1998，11:597－603.

［5］ J Jeswiet.A comparison of friction coefficients in cold rolling［J］.Journal of Materials Processing Technology，1998，80 －81:585－590.

［6］ H R Le，M P F.Sutcliffe.A robust model for rolling of thin strip and foil［J］.International Journal of Mechanical Sciences，2001，43:1405－1419.

［7］吴 迪，王贵桥，王敬东，等.钛板的张力冷轧研究［J］.东北大学学报:自然科学版，2008，29(10):1435 －1437.

(Wu Di，Wang Guiqiao，Wang Jingdong，et al.Investigation on cold rolling for titanium sheet under tensional effect［J］.Journal of Northeastern University:Natural Science，2008，29(10):1435 －1437.)

［8］ Wallace M.Bessa，Max S.Dutra，Edwin Kreuzer.Sliding mode control with adaptive fuzzy dead－zone compensation of an electro－hydraulic servo－system［J］.Journal of Intelligent＆Robotic Systems，2010，58(1):3－16.

［9］ Zhang Youwang，Gui Weihua.Compensation for secondary uncertainty in electro－hydraulic servo system by gain adaptive sliding mode variable structure control［J］.Journal of Central South University of Technology，2008，15(2):256－263.