构建基于小波熵的自训练半监督支持向量机分类模型评价老年人步态
2013-11-27吴建宁
吴建宁 伍 滨
(福建师范大学数学与计算机科学学院,福州 350007)
引言
当前,老年人跌倒的发生率高,已成为老年人致伤、致残、甚至死亡的主要原因之一。如何有效预防老年人跌倒,已成为众多学者探讨和关注的热点问题[1]。相关研究表明,人体步态(人体行走时的方式或姿态)与人体解剖结构、神经生理功能、运动控制能力等因素密切相关,在某种程度上反映人体行走功能的状况。特别在衰老期间,老年人受下肢骨骼肌肉功能下降、下肢关节柔韧性降低、前庭功能和平衡能力下降等生理因素的影响,其行走时步态功能下降,产生不稳定等危险步态,增大了他们跌倒风险。及早、准确地量化评价老年人步态,可有效降低老年人跌倒的风险[2-3]。
量化评价老年人步态变化的相关研究在生物力学等相关领域较早开展,并得到高度重视和广泛关注[4]。早期,相关学者运用步态分析方法,评价青年人和老年人在步速、步频、下肢关节角度变化范围及足-地反作用力等步态特征参数的差异,量化评价人体步态是否转入老年人步态[4-5]。随着步态分析系统技术和数据处理技术的快速发展,众多学者尝试将先进的数据处理技术用于各类步态数据分析中,有效鉴别青年人步态和老年人步态的差异,获取有效量化评价老年人的步态变化的技术手段,诸如基于人工神经网络构建步态分类模型被用来评价老年人的步态变化[6]。近年来,基于构建泛化性能优越的步态分类模型鉴别老年人步态模式来评价老年人的步态变化,已成为众多学者探讨的热点问题。从近年的文献报道来看,基于先进机器学习理论构建步态分类模型在步态分析中得到广泛应用。特别是基于有监督学习算法的支持向量机二分类模型,在量化评价老年人步态及其变化研究中持续受到关注和重视[7-11]。Begg等首次采用支持向量机二分类模型,通过鉴别12名健康青年和12名健康老年受试者的步态模式(由时空步态参数、运动学步态参数、动力学步态特征参数组成),量化评价了老年人的步态,并验证了小样本步态数据在支持向量机分类算法中的适应性[10]。Reginaldo等采用支持向量机分类算法,分析了17名健康青年和17名老年人的运动学步态数据,探讨了与年龄相关的老年人步态变化[11]。当前,基于有监督学习的支持向量机二分类算法来评价老年人步态的相关研究取得了积极的进展,但研究中仅考虑有标注步态数据类别间的差异信息,而忽略步态数据类内有价值的“内在信息”。另外,目前的研究仅局限于有标注的小样本步态数据,而忽略大量无标注步态数据在步态分类算法中的有效利用,特别是在大量无标注的老年人步态数据中,包含“有价值”的危险步态变异信息未得到有效利用,必将影响其泛化能力,降低学习算法的精度,难以准确评价老年人行走时的步态状况。事实上,在医疗环境中,获取大量有标注的人体步态数据比较费时费力,而获取大量的无标注的人体步态数据比较容易。如何寻找一种能有效利用大量无标注的人体步态数据,构建泛化性能优越的步态分类模型,准确量化评价老年人步态,是笔者研究的兴趣所在。
据近年的相关文献报道,基于半监督学习的支持向量机分类算法能够有效地利用大量无标注数据,较好地改善分类性能,并已在脑电、心电等生物医学信息处理中得到成功的应用[12-13],但在量化评价人体步态变化的相关研究中仍未得到应用。在研究中,笔者尝试应用半监督支持向量机分类算法来分析大量无标注的人体步态数据,旨在充分考虑利用步态数据类别间和步态数据内在“有价值”的步态变异信息,改善支持向量机步态分类算法的性能,准确评价老年人行走时的步态状况。近年来,自训练半监督支持向量机分类算法在生物医学信息处理中得到普遍重视[12-13]。在算法设计研究中,首要考虑的问题就是在自训练过程中如何从无标注生理数据中获取有标注数据,并且每次添加到样本训练集中标注的样本对于当前分类模型而言必须最具信息量,否则将严重影响分类器的学习能力[14]。为此,如何寻找一个能有效衡量步态数据样本信息量大小的有效参量,是设计步态分类算法非常重要的环节。基于人体步态数据的非平稳性、复杂性等特性以及前期的研究工作发现,小波熵能够有效表征人体步态系统内在的紊乱变化程度,能够获取更多表达人体步态变异的信息量[15]。基于上述思路,笔者提出了一种基于小波熵的自训练半监督支持向量机步态分类算法,旨在尝试采用基于小波熵从未标注步态数据中来挑选那些在当前分类器下最具信息量的样本,以提高自训练半监督支持向量机分类器的泛化能力,准确量化评价行走时的老年人步态。在研究中,采集了120名不同年龄组的未标注足-地反作用力步态数据,采用本研究提出的分类算法对其进行分析,并与基于有监督学习的支持向量机分类模型比较,以验证所提出的分类模型评价老年人步态的有效性和优越性。
1 构建基于小波熵的自训练半监督支持向量机分类算法
1.1 半监督支持向量机分类算法
半监督学习是一种近年来应用于模式识别等领域较先进的机器学习算法,其核心思想是依据光滑性假设,充分综合考虑利用数据类别间概率分布信息和数据类别内在结构分布信息,以改善传统监督学习算法中忽略数据所具有某种内在结构分布信息的不足,提高学习器的泛化性能[14]。通过对来自某种未知分布的一个有标注示例集X1={(xi,yi)(xi表示i个数据,yi是xi的类别标号),与一个无标注示例集X2={xi}进行学习,期望得到一个决策函数f:X→Y(X=(X1,X2),Y={yi}),能够对示例 xi准确预测其标记 yi。本研究采用yi∈{-1,+1},其中-1表示青年人步态模式,+1表示老年人步态模式。为了找到函数,通过任取一个满足Mercer定理的核函数K:X×X→R,对数据X=(X1,X2)映射,在产生与之对应的重构核Hibert空间(RKHS)中进行优化学习,使其具有最小值,即

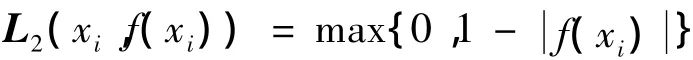
通过引入松弛变量ξ,可将式(1)表示为

为此,利用支持向量机算法(SVM),即可得到一个决策函数f:X→Y。
1.2 基于小波熵的自训练算法
考虑到步态数据与脑电、心电数据具有相同的高维性、非平稳性、复杂性等特性[6],采用自训练半监督学习算法在RSHK中寻找最优的决策函数。基本思路就是首先利用少量的有标注样本步态数据训练构建支持向量机分类模型,然后对无标注步态数据分类预测,选取新的有标注的步态数据添加样本训练集,构建新的样本训练集(由训练数据、无标注数据、新添加的标注数据组成),训练学习新的支持向量机分类模型,循环上述过程,不断更新样本训练集,直到得到最终的支持向量机模型,也就是直到获得泛化性能最优的步态分类模型为止。在自训练过程中,添加到样本训练集的样本标号与所选样本的真实类别标号是否一致至关重要。若不一致,可能产生的误差就会在迭代过程中不断积累,必将影响学习性能。为此,要求选取的样本数据对当前分类模型最具信息量,尽量减少在自训练迭代过程中可能产生的误差。在研究中,考虑到人体步态功能变异与人体步态系统内在紊乱变化程度密切相关的特性[15],尝试采用小波熵作为衡量从未标注步态数据中来挑选那些在当前分类器中最具信息量样本的有效参量。
首先计算小波熵值[15],也就是对步态数据进行多尺度小波分解,得到各分解层的小波系数{Dj(k),其中 m 为每个分解层小波系数的个数。根据所得小波系数,计算各分解层的能量分布及所有小波系数的能量之和,有

然后根据各分解层的能量计算相对小波能量,即

然后根据相对小波能量计算小波熵,有

然后依据前期研究工作[15],根据计算得到的健康青年和老年受试者步态数据小波熵值的统计差异,定义从未标注数据、挑选标注样本数据的阈值。青年和老年人的小波熵值变化范围分别定义为M±SD,其中M为平均值、SD为标准差,若有相冲突的数据则剔除。
综上所述,本研究提出基于小波熵的自训练半监督支持向量机步态分类算法,其流程框架如图1所示。

图1 基于小波熵的自训练半监督支持向量机分类算法流程框架Fig.1 The framework of the classification algorithm of the self-training semi-supervised support vector machine based on wavelet entropy
具体的算法主要包括4个步骤。
步骤1:用少量有标注的步态数据构建样本训练集,学习训练得到支持向量机分类模型,然后对无标注的步态数据分类,得到预测标注样本,并计算其相应的小波熵值,并依据小波熵阈值挑选一些新的标注步态数据。
步骤2:用训练样本数据、剩余的无标注步态数据、上一步得到的新的标注步态数据,构建一个新的样本训练集,再进行训练学习,得到一个新的支持向量机分类模型。同样,对剩余的无标注步态数据进行预测,计算预测样本的小波熵值,并依据小波熵阈值挑选一些新的标注步态数据。
步骤3:计算新的支持向量机相应的目标函数值,有

步骤4:k次迭代步骤2和步骤3。假定一个正常数δ0,计算第k次和k-1次的支持向量机相应的目标函数值,判断两者的绝对值是否小于δ0,若不小于δ0则继续k+1次迭代,若小于δ0则停止循环,从而得到测试样本的最终分类标注,即最后的分类结果。
2 实验分析
2.1 采集步态数据
由于研究中要采集大量未标注老年人步态数据,考虑到老年人受试者行走状况,所以设计受试者步态数据采集过程不仅要简单易行,并且采集的步态数据要能够包含更多与人体步态变异密切相关的本质信息。目前,在生物力学中有关的步态假说研究表明,足-地反作用力等动力学步态参数能体现人体步态的内在“动力链”,可较好地反映人体行走时下肢力量及步态变异状况[2,16]。为此,笔者采集了120名不同年龄组受试者的足-地反作用力步态数据,其相关生理参数如表1所示。在采集过程中,为避免各种干扰因素,要求受试者赤足按本人习惯或自然的步速在一个内嵌测力平台的实验水平步道上行走;为确保测力平台准确记录受试者步行时的足-地反作用力步态数据,要求每个受试者在步行时一只足尽可能地踏在测力平台的中间位置。采样频率为400 Hz,每个受试者记录3~5次满足条件的步态数据。在采集前,让受试者在实验水平步道上行走数次,以便熟悉数据采集试验环境和要求;同时,要求所有受试者熟悉和同意步态数据采集方案及相关事项[15]。
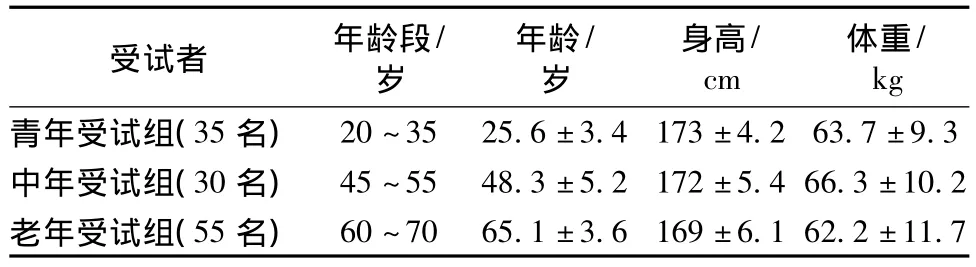
表1 不同年龄组受试者的生理参数(均值±标准差)Tab.1 The physiological parameters from the subjects groups with different ages(M±SD)
2.2 数据预处理
为消除受试者之间的个体差异,便于步态数据量化分析,对足-地反作用力步态数据进行归一化处理。将每个受试者足-地间反作用力除以其自身体重,即将每个受试者足-地反作用力归一化为其自身体重的百分比,以消除受试者自身体重所造成的差异;将每个受试者的足与地面的接触时间长度归一化为步态周期中支撑期的百分比,以消除受试者之间因不同步速所产生的差异。一名受试者的步态数据如图2所示,其中Fz为垂直方向力(vertical force),Fy为前后方向力(anterior-posterior force),Fx为左右方向力(medio-lateral forces))
2.3 确定小波熵阈值

图2 一名受试者在3个不同方向的足-地反作用力在支撑期的变化状况Fig.2 The change of the three different ground reaction force(GRF)during stance phase
在实验中,为便于小波变换计算,将一个支撑期数据长度处理为256个数据点,采用Daubechies6小波基函数对步态数据进行7尺度小波分解,计算相应的小波熵值。依据笔者在前期研究建立的健康青年和老年人数据库,由于垂直和前后方向的足-地反作用力步态数据蕴含较多的人体步态变异信息[2,5,16],所以选取 12 名健康青年受试者和 12 名健康老年受试者垂直和前后方向足-地反作用力步态数据计算小波熵值,并用t-检验法统计分析两组小波熵值差异(检验显著性水平值P<0.05,小波熵具有显著差异)。由于在上述两个不同方向足-地反作用力步态数据上,青年受试者比老年受试者在不同尺度上的相对小波能量分布较均匀(详见文献[15]),为了得到较好的标注数据,所以确定标注健康青年数据的小波熵阈值应大于统计分析的平均值,而标注老年数据的小波熵阈值应小于统计分析的平均值,其结果如表2所示。

表2 健康青年和老年受试组在垂直方向和前后方向反作用力步态数据分析结果Tab.2 The analyzed results obtained the vertical and anterior-posterior GRF from health young and elderly subjects
2.4 步态特征选取
由于支持向量机分类算法的泛化性能与表达数据的特征向量的维数大小密切相关,实验中为了较好地表达步态数据,分别从垂直方向和前后方向的足-地反作用力步态数据中,选取步态分析中常用的10个含有大量与人体步态变化密切相关特征信息的步态参数,构建步态模式特征向量[2,16](见图3),也就是将一个步态模式表示为10维的特征向量。其中,(a)为垂直方向力,主要有足跟着地时的最大承受力Fz1、与Fz1相应的时刻Tz1、全足着地时的最小承受力Fz2,与Fz2相应的时刻Tz2、足尖离地时的最大承受力Fz3、与Fz3相应的时刻Tz3;(b)为前后方向力,主要有足停止时最大承受力Fy1与相应的时刻Ty1、足离地时最大承受力Fy2与相应的时刻Ty2)。

图3 从垂直方向(a)和前后方向(b)力中选取的步态特征参数Fig.3 The gait features selected from vertical(a)and anterior–posterior(b)directional GRF during stance phase respectively
2.5 实验结果
首先选取20名(10名健康青年和10名健康老年)受试者的步态数据构建样本训练集,建立支持向量机分类模型,然后采用自训练算法对120名未标注受试者的数据进行预测和训练,另选取24名健康青年和24名健康老年受试者的步态数据作为测试数据,评估自训练过程中每次迭代的支持向量机分类性能。由于数据有限,每次迭代添加的标注样本数据数根据预测样本量大小及相应小波熵值而定,添加的标注样本数量可变。在实验中,起始添加的标注样本数量为6,设置调节参数C1=0.85,C2=0.2,利用 LIBSVM 实现 SVM 算法[17],采用线性核K(xi,xj)=xixj。为了比较,没有依据小波熵阈值选取添加的样本,而是根据每次的预测样本随机选取添加的样本,两种不同的添加样本方法(在每次迭代过程的添加的样本数相同)的分类性能如图4所示。可以看到,支持向量机分类性能随着添加的标注样本数增加逐步得到改善,迭代初期两种样本选取方法的分类性能相当,这可能由于此时样本训练集中的样本数较少,分类泛化性能差。随着迭代次数增加,基于预测样本随机选取添加的标注样本方法的泛化性能不稳定;而基于小波熵选取的标注样本方法的泛化性能明显优于前者,当迭代次数为12时,分类性能最优。上述结果表明,小波熵能够有效地从未标注步态数据中来挑选那些在当前分类器里最具信息量的样本,可有效提高自训练半监督支持向量机的泛化性能。

图4 两种不同的添加样本方法对分类性能影响的比较Fig.4 The comparison of the effect of classification performance on the two methods for samples added in training sample set
此外,为了比较步态数据对分类性能的影响,笔者采用文献[10]中的有监督学习支持向量机方法来评价不同方向反作用力步态数据,两种方法在不同方向的足-地反作用力步态数据的最优分类泛化性能如表3所示。可以看到,依据笔者提出的半监督步态分类算法,垂直方向和前后方向的足-地反作用力数据的分类正确率分别为85%和81%,基于两种不同方向的足-地反作用力相结合的步态数据的最大分类正确率为90%;相比之下,依据文献[10]的有监督步态分类模型,垂直方向和前后方向的足-地反作用力数据的最大分类正确率仅分别为83%和75%,基于两种不同方向的足-地反作用力相结合的步态数据的最大分类正确率为85%。结果表明,半监督支持向量机分类算法能够有效综合利用步态数据类别间和步态数据内在的“有价值”的步态变异信息,改善支持向量机步态分类算法性能,准确鉴别青年和老年人步态模式,为有效评价人体步态转为老年人步态状况提供依据。

表3 两种步态分类算法在不同方向力步态数据上的分类正确率Tab.3 The accuracy obtained by two gait classification algorithm based on two directional GRF gait data
3 讨论
实验结果表明,笔者提出的基于小波熵的自训练半监督支持向量机步态分类算法能够充分利用大量未标注步态数据,有效提高步态分类性能。在研究中,首先挑选了一些健康的青年和老年人受试者步态数据来定义小波熵阈值,从表2的统计分析结果来看,青年和老年的步态模式存在较大差异。为了有效评价小波熵从未标注步态数据中获取保持真实的标注样本数据,在未标注数据中添加了中年年龄段(45~55岁)的步态数据,主要考虑到该年龄段处于老年前期,受人体神经生理功能、运动控制能力下降等因素对步态功能的影响,步态功能易发生变异,其步态数据可能含有与老年人步态变化密切相关的特征信息,有助于准确评价老年人步态。目前,在应用半监督学习算法进行生物医学信息处理的研究中,众多学者针对不同的生物医学数据特性,探讨了如何从未标注数据中进行有效标注数据,以提高半监督学习分类算法的性能[12-13]。在研究中,针对步态数据的非平稳性、复杂性以及有效表达步态数据分布的特性,采用小波熵作为衡量从未标注步态数据中来挑选那些在当前分类器中最具信息量样本的有效参量。从图4的结果来看,随着基于小波熵阈值选取的添加标注样本数增加,基于半监督学习的分类算法性能不断增强,经过12次迭代以后,步态分类器的最终分类正确率逐步平稳,表明基于小波熵获取的添加样本能够较好地代表样本在特征空间的分布,12次迭代以后添加的样本对分类性能影响较小。然而,依据每次预测样本随机选取添加样本,构建自训练支持向量机步态分类器,其分类性能不稳定,这可能是由于在自训练过程中,添加到样本训练集的样本标号与所选样本真实类别标号不一致,产生的误差在迭代过程中不断积累,从而影响学习的性能。上述结果表明,小波熵能够有效地衡量从未标注步态数据中挑选那些在当前分类器中最具信息量的样本,改善半监督步态分类的泛化性能。
在研究中,仅考虑采用足-地反作用力的步态数据进行分析来评价人体步态变化。从表3的结果来看,基于笔者的算法和大量未标注的足-地反作用力数据,能够获得与文献[10](基于有监督学习支持向量机分类算法,同时采用时空步态数据、足-地反作用力步态数据、下肢关节角度步态数据)相近的最大分类正确率。仅从足-地反作用力的步态数据来看,采用笔者提出的分类算法得到的最终分类正确率高于文献[10]中的分类正确率5%,表明大量未标注的步态数据蕴含大量与人体步态功能变化密切相关的变异信息,对于改善步态分类算法性能和评价老年人步态极其重要。此外,分别对垂直和前后方向足-地反作用力数据进行分析。从表3中的结果看到,基于垂直方向的足-地反作用力步态数据的最终分类正确率明显优于基于水平方向足-地反作用力步态数据的最终分类正确率,说明垂直方向足-地反作用力中的步态特征参数(如足跟着地时的最大承受力Fz1、全足着地时的最小承受力Fz2等)能够提供更多的表达转化为老年人步态的变异信息,这个结果与文献[2,5,16]的研究结果一致。
4 结论
本研究提出的基于小波熵的自训练半监督支持向量机步态分类算法,能够充分利用大量未标注的足-地反作用力步态数据,获取步态数据内在与人体步态功能变异密切相关的有价值信息,改善步态分类算法性能,准确鉴别青年和老年的步态模式,可有效评价人体步态变化,为量化评价老年人步态提供了新思路和新方法。今后的工作尝试是将本研究提出的算法应用于时空步态数据、运动学等不同类型步态数据的分析,进一步探讨老年人步态变异机制的相关研究内容。
[1]中华人民共和国卫生部疾病预防控制局.老年人跌倒干预技术指南[EB/OL].http://www.moh.gov.cn,2011-09-06/2012-11-20.
[2]Giannini S,Catani F,Benedetti MG,et al.Gait analysis:Methodologies and clinical applications[M] //Benedetti MG,eds.Terminology,Parameterization and Normalization in Gait Analysis.Amsterdam:IOS Press,1994:65 -88.
[3]Brach JS,Perera S,Studenski S,et al.Meaningful change in measures of gait variability in older adults[J].Gait and Posture,2010,31(2):175-179.
[4]Nigg BM,Skleryk BN.Gait characteristics of the elderly[J].Clinical Biomechanics,1988,3(2):79-87.
[5]François P,Hélène C,Réjean H.Gait in the elderly[J].Gait and Posture,1997,5(2):128-135.
[6]Chau T.A review of analytical techniques for gait data.Part 2:Neural network and wavelet methods[J].Gait and Posture,2001,13:102-120.
[7]Wu Jianning,Wang Jue,Liu Li.Feature extraction via KPCA for classification of gait patterns[J].Human Movement Science,2007,26(3):393-411.
[8]Begg RK,Palaniswami M,Owen B.Support vector machines for automated gait classification[J].IEEE Trans on Biomedical Engineering,2005,52(9):828-838.
[9]Khandoker AH,Lai DT,Begg RK,et al.Wavelet-based feature extraction for support vector machines for screening balance impairments in the elderly[J].IEEE Trans on Neural Systems and Rehabilitation Engineering,2007,15(4):587-97.
[10]Begg RK,Kamruzzaman J.A machine learning approach for automated recognition of movement patterns using basic,kinetic and kinematic gait data [J].Journal of Biomechanics,2005,38:401-408.
[11]Reginaldo K,Fukuchi B,Bjoern M,et al.Support vector machines for detecting age-related changes in running kinematics[J].Journal of Biomechanics,2011,44(3):540 -542.
[12]尧德中,刘铁军,雷 旭,等.基于脑电的脑-机接口:关键技术和应用前景 [J].电 子 科 技 大 学 学 报,2009,38(5):550-553.
[13]王金甲,贾敏.标签均值的自训练半监督支持向量机用于EEG分类[J].中国生物医学工程学报,2011,30(5):666-672.
[14]Chapelle O,Scholkopf B,Zien A.Semi-supervised Learning[M]//JoachimsT,eds. Transductive SupportVector Machines.Cambridge:MIT Press,2006:101 -112.
[15]吴建宁,伍滨,王珏.用小波熵评价人体步态变化[J].航天医学与医学工程,2009,22(6):437-442.
[16]Begg RK,Rahman SM.A method for the reconstruction of ground reaction force-time characteristics during gait from force platform recordings of simultaneous foot falls[J].IEEE Trans on Biomedical Engineering,2000,47:547-551.
[17]Chang CC,Lin CJ.LIBSVM:a library for support vector machine[EB/CP].http://www.csie.ntu.edu.tw/~ cjlin/libsvm,2009-05-01/2012-11-20.
