伪噪声码承载卫星导航电文的潜行器——GNSS卫星的运行轨道之二

武汉大学测绘学院 刘基余

20世纪40年代末期，信息论的奠基人香农（C.E.Shannon）首先指出，白噪声形式的信号是一种实现有效通信的最佳信号；但因产生、加工、控制和复制白噪声的困难，香农的设想未能实现。直到20世纪60年代中期，伪随机噪声编码技术的问世，噪声通信才获得了实际的应用，并随即扩展到了雷达和导航等技术领域。在GNSS卫星导航应用中，伪随机噪声码（简称为伪噪声码）是卫星导航电文（即数据码D(t)）的承载体，两者通过模二和加法器（以⊕示之）而成为一种扩频码（如图1所示），进而对L波段载波进行数字调相，形成向广大用户发送的导航定位信号。本文主要论述伪噪声码在GNSS卫星导航应用中的相关理论及其实用问题。

一、伪噪声码的运算规则

噪声通信，是采用伪随机噪声码（Pseudo Random Noise Code，简称为伪噪声码，也称之为伪码）。卫星导航所用的伪噪声码，是噪声通信的成功实践。所谓伪噪声码，简而言之，是一个具有一定周期的取值0和1的离散符号串，它具有类似于白噪声的自相关函数。图2表示一种极简单的伪噪声码，它具有两种表述形式：信号波形和信号序列。其中，τ0是以秒为单位的码元宽度；TP是以秒为单位的时间周期，且知TP＝LP×τ0，此处LP是长度周期，也即在一个时间周期内的码元数目；本例LP＝7，也有用比特作为长度周期的单位（图示为7比特的长度周期）。在二进系中，信号序列称为二进符号序列，记作｛x｝；信号波形叫做二进信号波形，以x(t)表示之。两者的相应关系如表1所示。根据所研究的问题不同，选用不同形式来表述伪噪声码。

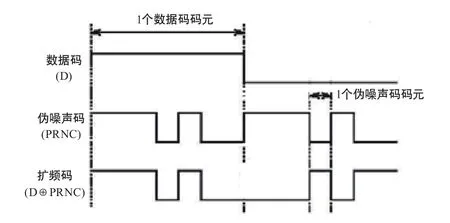
图1 扩频码的形成

图2 伪噪声码的表述形式

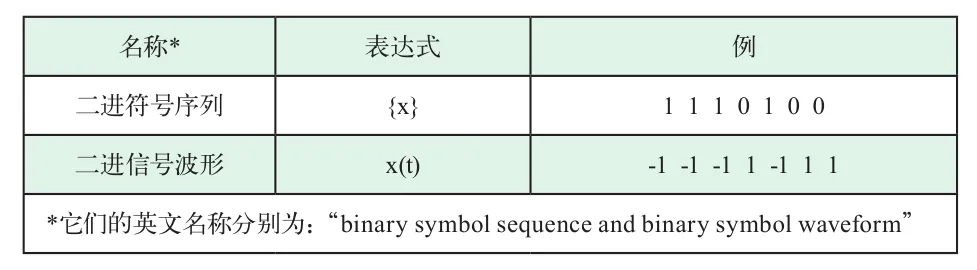
表1 伪噪声码的二进表述法

当对二进符号序列作模二和（不进位加，它以⊕表示）时；遵循下列规则：

当对二进信号波形进行相乘运算时，依据下列规则：

上述两种运算方法是等效的，记作

值得注意的是，上述运算法则只适应于二进符号序列（波形）。

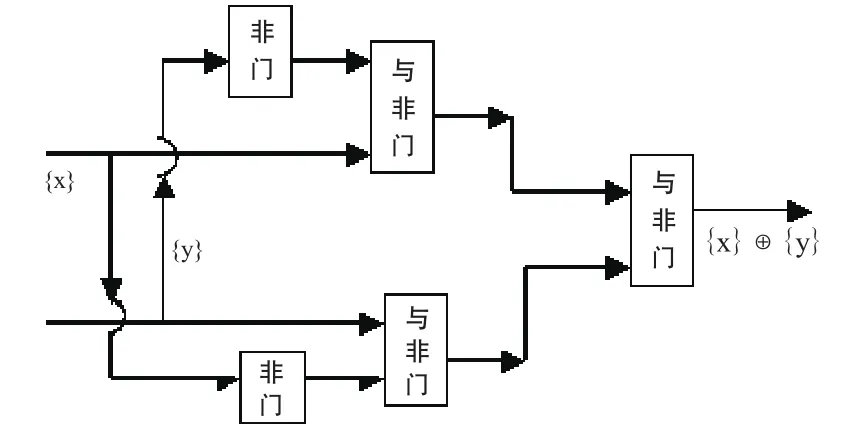
图3 模二加法器框图

此处，｛x｝和｛y｝分别表示两个序列，x(t)和y(t)则为两个相应的波形。图3表示模二加法器的基本构成；它的输入和输出高电平均为“0”示之，它的输入和输出低电平均以“1”表示，用高低电平两种工作状态，实现二进数字“0”和“1”的模二和运算。

二、伪噪声码的产生

移位寄存器，是产生伪噪声码的基础电路。移位寄存器不仅具有暂时存放数据和指令的功能，而且具有移位功能。所谓“移位功能”，是寄存器中所存放的数据，可以在移位脉冲的作用下，逐次向左移动或向右移动。

移位寄存器的寄存器单元，一般采用D型触发器（如图4所示），其工作特点是，输出状态等于现时刻的输入状态。图4中的D=1表示输入高电位，D=0表示输入低电位；输入电位为工作状态的建立创造条件，而建立状态的具体时刻则由时钟脉冲CP来决定；即，时钟脉冲CP是用来控制工作状态转移的发生时刻。在时钟脉冲CP的作用下，D型触发器可以将它的输入状态转移到输出状态，而实现数据移位。

如果将若干级（个）D型触发器按一定方式联接起来，便构成一个移位寄存器，图5是一个由4个D型触发器构成的四级移位寄存器。若在其输入端输入某一个数码（电位状态），当时钟脉冲（移位脉冲）串的第一个脉冲（常叫做第一拍）来到时，该数码便从触发器TR1的输入端转移到TR1的输出端（即触发器TR2的输入端）；同理，在第二、三、四个时钟脉冲的作用下，这个数码将从触发器TR2的输入端依次转移到触发器TR3的输入端、触发器TR4的输入端和输出端，而将一个四位数码全部移入寄存器。

图4 D触发器

图5 四级移位寄存器框图

伪噪声码的产生，不能用一般的移位寄存器，而必须采用一种具有特殊反馈电路的移位寄存器，叫做最长线性移位寄存器（其反馈电路是线性的），或叫做抽头式反馈移位寄存器（它的英文名称为：”tapped feedback shift register’and/or’maximal-length linear shift register”），它所产生的伪噪声码也叫做m序列。图6表示一个四级最长线性移位寄存器，或称四级m序列发生器。它包括四个D型触发器（D1D2D3D4）、模二和反馈电路和时钟脉冲产生器；图中的置“1”脉冲，将使m序列发生器的各个触发器之初始状态均为“1”，称之为全“1”状态。｛xf｝表示反馈到触发器D4的序列，该反馈序列是触发器D1D2输出脉冲串的模二和。所需要的m序列｛x0｝是从触发器D1输出的。

图6 m序列发生器的方框图

m序列｛x0｝的产生过程如下述。当时钟脉冲的第一拍（脉冲）来到时，Di的“1”状态，将转移到Di-1（此处i=4，3，2，1）。因为D1D2两个触发器均处于“1”状态，它们的输出脉冲之模二和为“0”；它被反馈到触发器D4的输入端（见图6所示）；故表1中状态栏内的第二列D4处于“0”状态。当第二拍时钟脉冲来到时，D4的“0”状态被转移到触发器D3，致使后者从“1”状态变成“0”状态；D1D2输出脉冲的模二和仍为“0”，它依旧被反馈到D4的输入端，致使D4D3D2D1的状态分别为0011。在第三拍时钟脉冲的作用下，D3的“0”状态转移到D2触发器，D1D2输出脉冲的模二和还为“0”，致使D4仍处在“0”状态，故知D4D3D2D1分别处在0001状态。在第四拍时钟脉冲的作用下，触发器D4D3D2D1便分别处在1000状态。如此类推，直到第十五拍时钟脉冲来到时，移存器的各级又处在“全1”状态（见表2）。在时钟脉冲的作用下，周而复始地重复着上述状态过程；因此，触发器D1的输出端便输出一个长度周期为15比特的m序列：

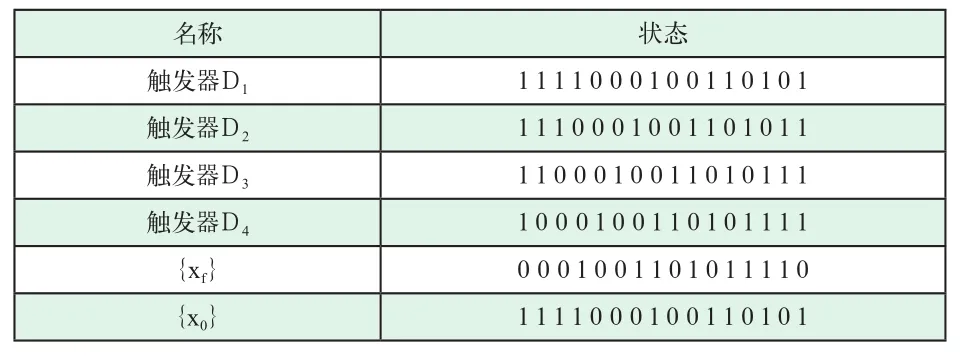
表2 m序列发生器的状态表

上述序列是用触发器D1D2输出脉冲的模二和构成的反馈序列，故图6所示的线性反馈移位寄存器的特征多项式记作

式中，x的肩标（1，2）表示从那一级（D1D2）抽头。

图7 变换输出的序列发生器

表3 几种不同的输出序列

如果图6的反馈电路和m序列输出予以变化，便得如图7所示的序列发生器。在图7的情况下，该发生器的特征多项式为

表3列出了图7所示移存器的各级状态；由该表可见，图6和7两个发生器的反馈序列虽相同，但在图7的发生器中，输出序列是从触发器D1D4引出而经一个与门输出的，故其输出序列为

如果图7所示的发生器不是从D1D4通过与门输出序列，而是从D2D4通过与门输出序列，则有新的输出序列

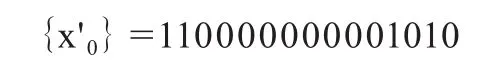
图7中的反馈序列若不是取自DE1D4，而是用D1D4，此时反馈序列和输出序列分别为

当用D1D4获取反馈序列时，输出序列不是触发器D1D4引出，而是从D2D4引出而经过一个与门输出，则有

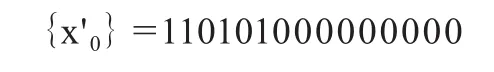
如果取消图7中的与门，而从D1触发器直接输出序列，则得到和图6从D1触发器直接输出的相同序列，即一个长度周期为15比特的m序列

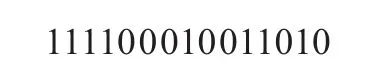
图6所示的四级m序列发生器，若仅改变它的反馈联接方式（如图8所示），则可得到不同结构的m序列。比较图6和图8所输出的m序列可见，两个输出序列具有相同的周期，但两者的结构不同。由此可见，m序列的结构仅取决于m序列发生器的反馈联接方式。不同的反馈联接方式，产生不同的m序列。若用移位算符X的j次方表示从m序列发生器第j级的输出，且以Cj＝0或Cj＝1表示第j级的输出没有连接到或连接到模二加法器，以C0＝0，或C0＝1表示模二加法器的输出没有连接到或连接到第一级输入端；这样，线性反馈联接方式由下列多项式f(x)表述

公式（4）被称作m序列发生器的特征多项式。图8所示m序列发生器的特征多项式为

依据图6和图8所产生的m序列，可见其具有下列特性：

（1）n级移位寄存器所产生的m序列之码元宽度等于时钟脉冲的周期τ0；m序列的长度周期LP=2n-1（此处n为移位寄存器的级数），时间周期TP=LP×τ0=(2n-1)τ0；图6和图8所产生的m序列之LP=（24-1）=15bits。

（2）在m序列一个周期中，“1”的个数比“0”的个数多1，即“0”元素出现（2n-1-1）次，“1”元素出现2n-1次，而具有平衡性。

（3）对一个周期的m序列，能够得到一个结构不变的另一个等价平移m序列；例如，m序列｛x｝=111101011001000和该序列的平移序列｛xτ0｝=011110101100100之模二和，得到下列等价平移m序列｛x4τ0｝：

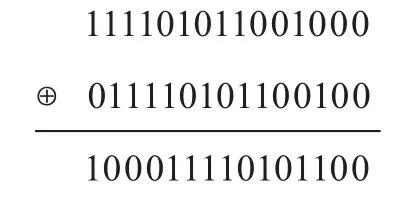
如果平移序列从原来的向前移变成向后移，则有

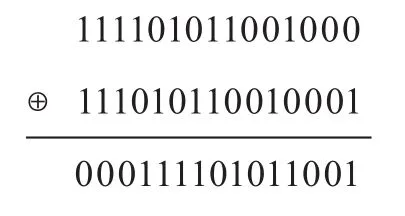
从上述两例可见，不论是向前移的平移序列，还是向后移的平移序列，它们与原序列的模二和，其结果都是一个结构不变的等价平移m序列。

（4）m序列具有良好的相关性。在一般情况下，若有两个相同时间周期T的序列x1(t)和x2(t)，则两者之间的互相关系数定义为

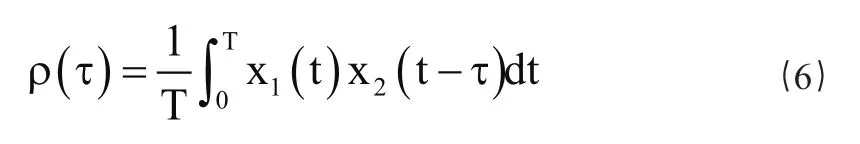
式中，τ是x2(t)相对于x1(t)的时间延迟。当x1(t)=x2(t)时，ρ(τ)就是自相关系数；通俗地说，相关系数ρ(τ)表示序列x1(t)和x2(t)之间的“相似”程度。对于时元tK的离散采样的自相关系数为

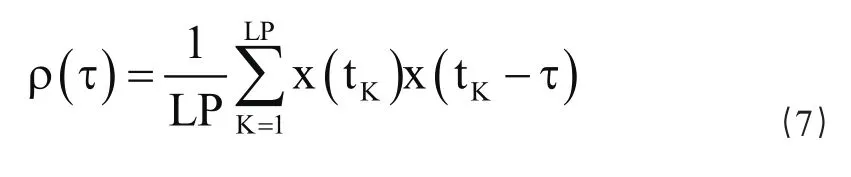
图8 变换反馈的m序列发生器

上式中的x(tK)x(tK-τ)，按前述二进信号波形乘积法则进行运算求得。对于m序列而言，它的自相关系数是

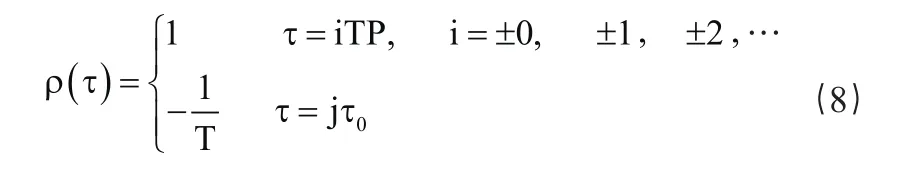
上式中，j等于除j不为0和LP的整倍数以外的任何数。上式的图解如图9所示，从该图可知，当τ从0趋近于码元宽度τ0时，自相关系数ρ(τ)从1趋近于-1/LP；当τ从(LP-1)τ0趋近于时间周期TP时，ρ(τ)则从-1/LP趋近于1；这种变化是具有周期性的。这和随机序列（无周期序列）的自相关系数δ(t)之形状是相似的；仅后者的δ(t)趋近于无穷大，其余各处均为0，且不具备周期性。因此，m序列又被称为“伪随机序列”，它具有双值自相关特性。

图9 m序列的自相关系数

m序列的互相关系数是不同结构m序列之间的相关系数，它是这样计算：先用模二和（或波形积）求出两个m序列｛xn｝和｛yn-τ｝的新序列；将后者中“0”的个数（表示｛xn｝和｛yn-τ｝相一致的码元数）减去“1”的个数（表示｛xn｝和｛yn-τ｝｝相异的码元数），除以新序列的码元总数，便得到m序列的互相关系数

例如，现有两个m序列｛x15｝=111100010011010和｛y15-τ｝=111101011001000，求它们的互相关系数

（a）当τ=0时

在新序列中，有11个“0”，有4个“1”，故知

（b）当τ＝τ0，即｛y15-τ｝的首位移到最后一位时，求两者的互相关系数

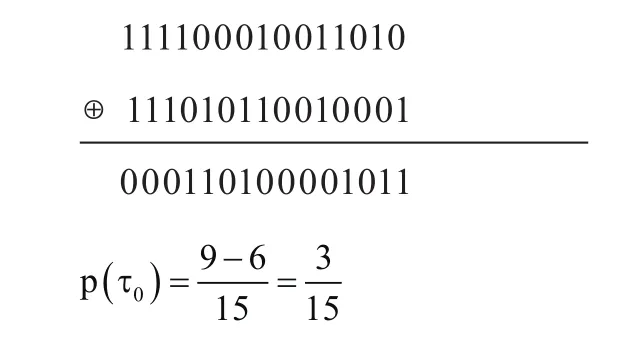
（c）当τ＝-2τ0，即｛y15-t｝的末两位数次移到首两位时，求两者的互相关系数：

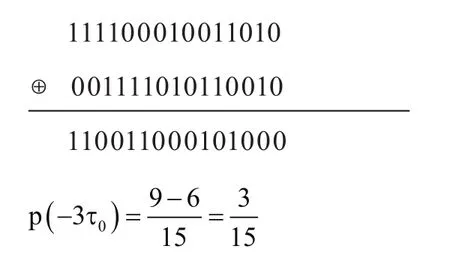
用上述计算方法不难证明，即使两个结构相同的m序列，如果两者之间存在时延τ，它们的互相关系数总是小于1的；只有调整其中一个m序列，致使它们之间时延τ等于零，即两个m序列的码元“对齐”，此时它们的互相关系数方才等于1；这是一个极为重要的实用特性。GPS信号接收机恰好利用互相关系数为最大值的特性，捕获、跟踪和识别来自不同GPS卫星的伪噪声码，解译出它们所传送的导航电文。

（5）根据m序列的自相关系数，可以求得它的功率谱为

式中，τ0为每个码元的持续时间；LP为m序列的长度周期。

从上式可见，m序列和随机序列一样具有(sinx/x)2型的频谱包络；但因m序列是周期性的，其频谱不再是连续的，而是以（2π/LPτ0）为间隔的离散状频谱。

三、几种特殊伪噪声码

正如前文所述，n级线性移位寄存器能够产生长度周期LP＝2n-1的m序列。在实际应用中，有时要求所用m序列的长度周期短于LP；有时要求所用m序列的长度周期长于甚至远长于LP。这就是下面要论述的截短伪噪声码和复合伪噪声码。

1.截短伪噪声码

在一个长度周期为LP的m序列中，若截取它的一部分码元组成长度周期为LP'的新序列（LP'＜LP），该序列叫做m序列的截短序列，或称截短伪噪声码（简称为截短码）。例如，为了获得一个长度周期LP'＝11的新序列，可以从长度周期LP＝15的m序列中截除一个子序列而获得该新序列；其具体方法是，在产生15bits m序列的四位线性移位寄存器中，增加一个状态检测器（0011），使其输出脉冲馈送到模二加法器（如图10所示）；只有当移位寄存器处于0011状态时，状态检测器的输出才为“1”，移位寄存器处于0011以外的任何状态，检测器的输出均为“0”。这个“0”输出加到模二加法器后，不会导致它的输出变化，只有状态检测器输出为“1”时，才导致模二加法器的输出由“0”变为“1”；即，一个4级m序列发生器，附加上一个0011状态检测器以后，导致该m序列发生器从0011状态跃变到1001状态（如表4所示），这相当于在原输出序列中“截除了”1000子序列，故从触发器D4输出的截短码为

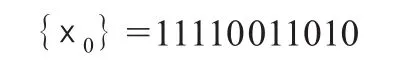
综上所述，截短伪噪声码是在一个m序列中截除一个子序列而形成的，其关键在于选取适宜的检测状态（如上例中的0011状态）；在《伪噪声编码通信》一书（钟义信编著，人民邮电出版社出版）中的表4～17列述了几比特至二千余比特的检测状态，可供使用参考。

图10 11bits截短码发生器

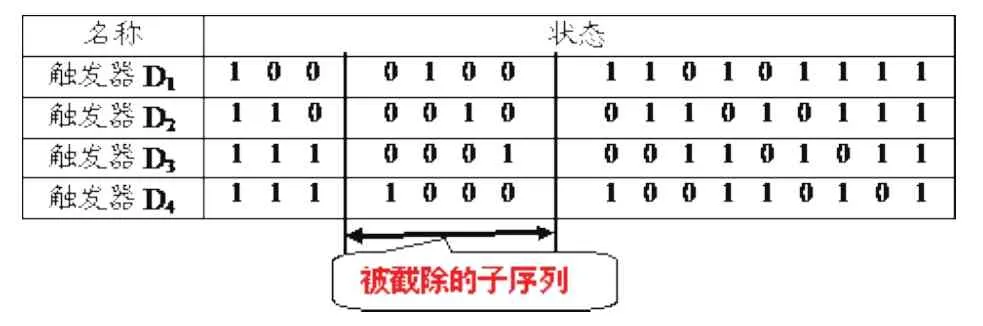
表4 截短序列状态

2.复合伪噪声码

在实际应用中，往往需要长度周期很大的m序列，而采用二个或二个以上的m序列构成复合伪噪声码。例如，一个长度周期为15bits的伪噪声码，若其码元宽度为τ0＝1×10-7s，则该伪噪声码的一个时间周期TP相应于长为450m的距离。当用它作距离测量时，只能单值地测得450m以内的距离。为了单值的测得远于甚至远远于450m以上的距离，一般采用增大伪噪声码长度周期的方法；也即用复合伪噪声码作测距信号。复合伪噪声码（简称为复合码），是由二个或二个以上的周期较短的伪噪声码（叫做子码）构成的。若n个子码的周期分别为P1,P2,…Pn，且Pi≠Pj时，由它们构成的复合码之周期为

上式表明，复合码的周期比子码的周期要长得多。例如，由长度周期分别为11bits和15bits的两个子码构成一个复合码，其长度周期为165bits；当其码元宽度τ0仍为1×10-7s时，该复合码的时间周期相应距离长达4950m，它较15bits子码增大了11倍。因此，复合码获得了较广泛的应用。

现以两个子码为例，说明如何获得复合码。为了节省篇幅，此处仅用两个极简单的子码，即，子码｛x｝＝1110100和子码｛y｝＝110，试求由它们构成的复合码｛z｝。其方法如下述：

（1）按式（11）求出复合码的周期Pz，即

（2）求出复合码的序列｛z｝；其方法是，将子码｛x｝重复书写3次，而子码｛y｝重复书写7次，两者依次排列而进行模二和运算，其结果便是所需求的复合码｛z｝：

图11和图12分别表示21bits复合码的波形和生成。从图示可见，若用两个子码构成一个复合码时，可将子码｛x｝重复Pz／PX次，再将子码｛y｝重复PZ／PY次，然后逐一地求对应码元的模二和，便得到复合码

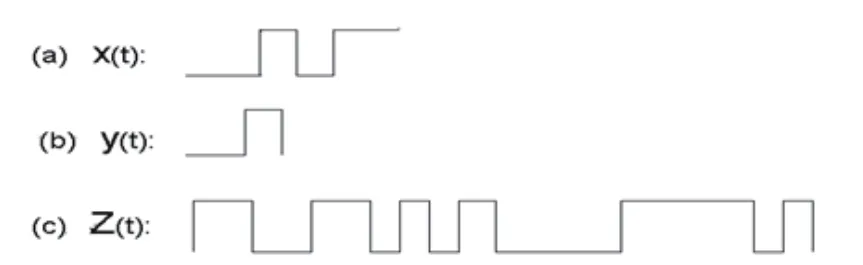
图11 复合码的波形

涉及复合码的另一个实用问题是，从已知的复合码及其中的一个子码，解译出另一子码，称之“解码”；其方法是按下式求得另一个子码：

式中，｛z｝为已知的复合码；｛y｝为已知的子码；｛x｝为待求出的子码。

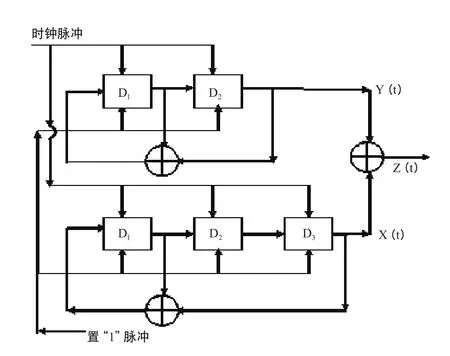
图12 复合码发生器之例

为了验证上式，现以一个最简单的复合码｛z｝＝001100101011111000010及其子码｛y｝＝110为例，解译出构成该复合码的另一个子码｛x｝，其方法如下

从上可见，解码的过程是，将已知子码｛y｝重复书写Pz／Py次，且与复合码的码元一一对齐，而求出它们的模二和。另一个待求子码｛x｝的周期为Pz／Py，故知模二和的结果中有Py个待求子码｛x｝；即在上列的模二和结果中具有三个周期的子码｛x｝，且知｛x｝＝1110100，这是图11中的第一个子码。由此可见，即使机密隐藏在某一个子码中，也可通过“解码”求得该子码，进而破译出隐藏的机密。

3.Gold组合码

1967年10月，美国学者R.Gold提出了一种组合码，并被命名为Gold码。它是由两个周期和速率相同而码元结构不同的m序列组合而成的。例如，现有具有相同周期LP＝2n-1的两个m序列：｛X｝和｛Y｝，则由它们构成的Gold序列为

式中，｛Yj｝为向左移动了j个码元的｛Y｝序列，而j＝0，1，2，… (2n-2)。

从式（14）可见，由两个m序列｛X｝和｛Y｝以及左移j个码元的｛Yj｝，可以构成（｛X｝⊕｛Y｝），（｛X｝⊕｛Y1｝）,（｛X｝⊕｛Y2｝）,…（｛X｝⊕｛Y2n-1｝）共（2n-1）个Gold序列，连同原序列｛X｝和｛Y｝，总共有（2n+1）个序列，叫做Gold序列族。

从上可见，Gold码具有下列特点：

（1）Gold码的速率和周期与构成它的m序列相同（如式（14）所示）。

（2）Gold码不是m序列，它的互相关值可用Anderson导出的下述公式进行估算

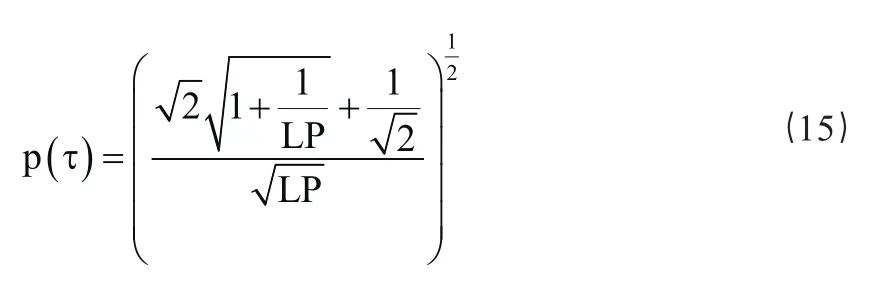
式中，LP为Gold码的长度周期。

（3）Gold码的结构简单，调整方便，具有大量的可用码型，适宜于码分多址的大量用户需求。n级移位寄存器能够产生独立的m序列数目为

式中，ψ(2n-1)为尤拉函数，其数值等于1，2，3，…2n-2数值中与（2n-1）为互素的正整数之个数；例如ψ(6)，在1，2，3，4，5诸数中，只有1，5两个数与6为互素。表5列出了2～15级线性移位寄存器产生独立的m序列数目。由表列数据可知，10级线性移位寄存器只能产生60个独立的m序列；然而，两个10级线性移位寄存器却能产生1025个Gold码，可供1025个用户作码分多址应用。因此，GPS卫星采用了Gold码作为易捕码（C/A码）。

表5 n级线性移位寄存器产生的m序列数目

图13 C/A码承载卫星导航电文的形成

四、结束语

伪噪声码，是一个具有一定周期的取值0和1的离散符号串，它具有类似于白噪声的自相关函数。伪噪声码是利用一种抽头式反馈移位寄存器而产生的，这种移位寄存器所产生的伪噪声码也叫做m序列。在后者的基础上，研发成功了Gold码，它被GPS卫星用作易捕码（C/A码）；C/A码承载卫星导航电文形成过程如图13所示。由图可知，GPS卫星向广大用户发送的导航信号，是经过了两级“调制”的调相波。这也是现代GNSS卫星借鉴的导航信号形成方法，而被广泛采用。

综观GNSS卫星导航所用，伪噪声码的主要用途可概括为下述三方面：一是伪噪声码在模二和加法器的作用下，与GNSS卫星导航电文形成扩频码，进而发送给广大用户；二是伪噪声码是GNSS用户用来测量站星距离的信号，人们常称之为“测距码”；三是在码分多址（CDMA）信号体制下，伪噪声码是区别不同GNSS卫星的依据，用以实现多颗在视卫星的有效接收和跟踪测量。