舰船波浪运动加速度积分误差纠正与预报
2013-11-26陈爱国王成勇叶家玮
陈爱国,王成勇,叶家玮
1)广东工业大学机电工程学院,广州510090;2)广州航海学院船舶工程系,广州510725;3)华南理工大学土木与交通学院,广州510640
为解决海上舰船或平台的波浪运动检测难以找到合适参照系的问题,本课题组前期研究基于加速度计阵列的船舶波浪运动检测原理[1],建立静坐标系OXYZ、平移坐标系 QXpYpZp和连体坐标系QXsYsZs,通过理论推导提出一种加速度计阵列,如图1.在Q点采用一个3轴加速度计,在A、B和C点各采用一个2轴加速度计,通过加速度计直接检测出aA_YS、aA_ZS、aB_XS、aB_ZS、aC_XS、aC_YS、aQ_XS、aQ_YS和aQ_ZS,已知各测量点之间的距离rAQ、rBQ和rCQ,由式(1)可计算出船舶横摇、纵摇和艏摇的角加速度

图1 加速度计配置图Fig.1 Configuration of acceleration indicators
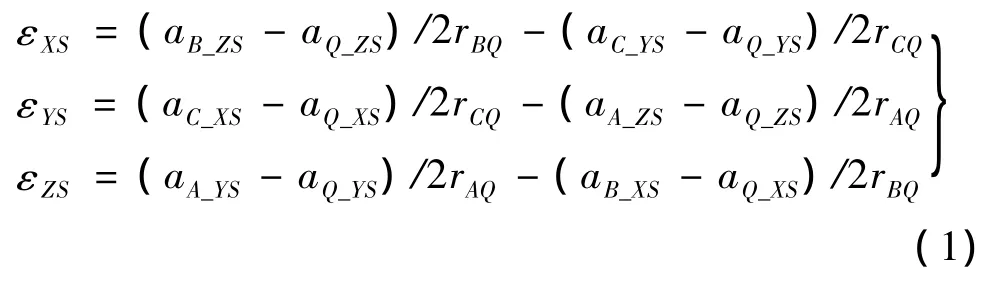
由式(2)可计算出船舶横摇、纵摇和艏摇的角速度

设船体上任意一点M,相对基点Q的位移矢量为r,r在QXsYsZs坐标系中的3个分量为rXS、rYS和rZS,根据式(3)可计得任意坐标点M处在连体坐标中的三向加速度,再通过坐标变换可计得任意点M在静坐标系下的加速度为[1]
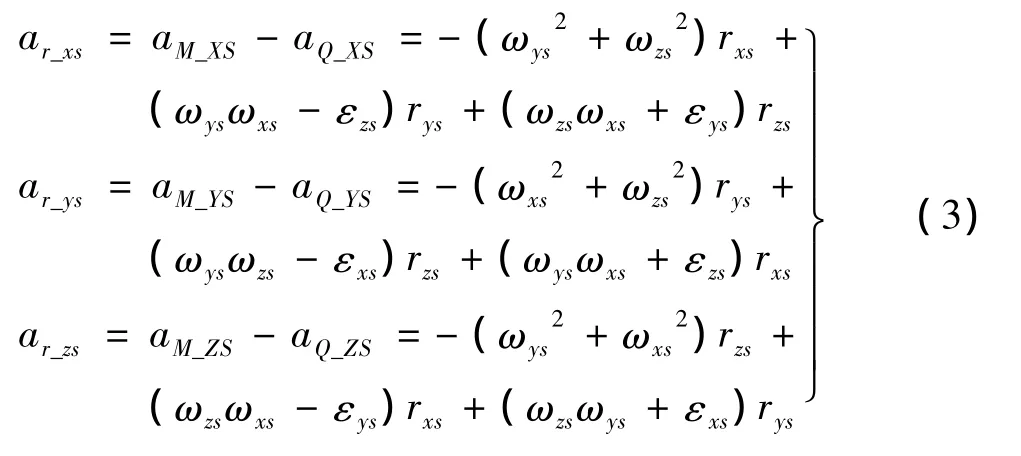
由于舰船波浪运动补偿一般采用位移补偿或速度补偿策略,船舶任意坐标点处的速度和位移通过对加速度进行数值积分得到,积分方式包括时域积分和频域积分.但仅进行简单的积分累积误差巨大.
为解决基于加速度计阵列的船舶波浪运动检测中加速度积分累积误差过大这一工程难题,真正建立用于工程实践的船舶波浪运动数据采集系统,文献[2-4]设计和构建液压驱动的船舶波浪运动模拟平台,以采集时间间隔st=0.01 s,采样频率sf=1/st=100 Hz,对加速度计B采集到2 744个数据,采集的原始实验数据如图2.通过对所检测加速度数据进行频谱分析和积分处理,分析加速度数据积分中直流分量、低频分量、高频分量和积分常数项对积分误差的影响,介绍其误差消除方法;并通过对实测加速度数据的时域积分、频域滤波后时域积分和全频域积分处理方法的研究,提出如图3的有效处理流程.研究表明,采用全频域积分处理方法是解决其中积分误差过大问题的最佳选择[2-4].

图2 加速度计B测量的加速度数据Fig.2 Acceleration data measured by the accelerometer B
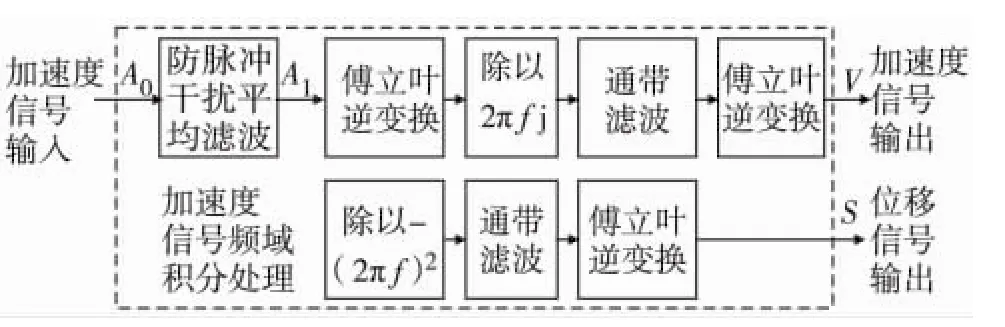
图3 实测加速度频域积分处理框图Fig.3 Flow chart of acceleration data integral processing in frequency domain
但研究也表明,在采样时段首尾端,由于数据长度的有限性和谱泄露,仍存在偏大的积分幅值误差,如图4和图5[5].
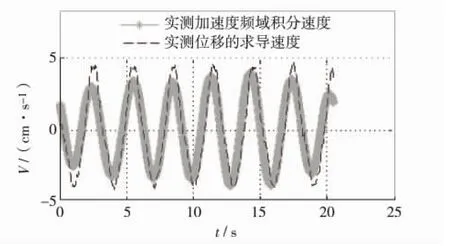
图4 实测加速度频域积分速度Fig.4 integral velocity of the measured acceleration in frequency domain
本研究采用舰船波浪运动预报技术针对实测加速度或积分数据进行波浪运动预报,修正积分末端误差,来获得更好的积分效果.应用舰船波浪运动预报技术还能预测未来的波浪运动情况,对于解决舰船过驳波浪补偿机构的大惯量延迟问题具有重要意义[6-9].
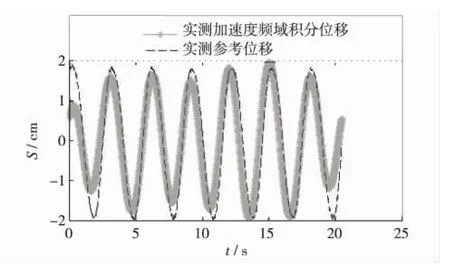
图5 实测加速度频域积分位移Fig.5 Integral displacement of the measured acceleration in frequency domain
1 频谱预报技术的理论基础
对于舰船波浪运动检测实时系统,通常采用频域积分技术.而针对频域特点,采用频谱预报技术便是首要选择,这样预报与积分技术可以很好结合,节省计算处理时间.
设{X*(n),n=1,2,…,N}为观测到的舰船波浪运动积分数据序列,此数据系列必然包含其周期性变化成分和随机变化成分,因此,可设

其中,{P(n),n=1,2,…,N}为周期性变化的序列项,它表明舰船波浪运动按周期变化的趋势;{X(n),n=1,2,…,N}为随机序列项[10-20].
针对本舰船波浪运动模拟平台检测的加速度积分速度和位移,P(n)仅由1个谐波函数组成,即

其中,ω1是谐波的角频率;To为采样时间;nTo为采样时刻,n=1,2,…,N;α为复数,其模表示谐波振幅,相角α代表谐波的初始相角.因此,式(4)可改写成式(6)形式

并简记为

其中,


2 舰船波浪运动加速度积分速度频谱预报处理
2.1 加速度积分速度频谱预报初步处理
鉴于加速度频域积分速度首尾端数据的幅值偏小较多,对图3中实测加速度频域的积分速度数据首尾各切去1个周期,把剩下的中间数据按式(6)用最小二乘法计算,使目标函数最小.因设定的舰船波浪运动模拟平台运动周期约为3 s,采样时间为0.01 s,因此用于计算目标函数的数据点为n=301,302,…,1 748.
在积分过程中,对实测加速度按FFT变换和滤波,并已按式(10)处理过的数据(即傅立叶逆变换之前的速度在频域内的频谱序列,

其中,A为加速度数据;V为速度数据.计算最大功率处的频率和相位,计得最大功率为5.664 7×103cm2/s3,为第8个数据点,此时的频率为(8-1)×df=7×100/2 048=7×0.048 828=0.341 769 Hz,相位为0.789 3 rad.在第301~1 748个速度数据点范围内速度幅值的平均值为3.634 cm/s.
由此,可设计算采用的初始预报速度为

其中,n=1,2,…,2 048,T0=0.01 s.结果如图6.
2.2 积分速度频谱预报

图6 舰船波浪运动预报积分初速度Fig.6 Original integral velocity of ship wave movement forecasting
基于式(11),在以速度幅值3.634 cm/s、频率0.341 769 Hz、相位 0.789 3 rad 为中心的小区域内,按式(9)在301~1 748区间以最小二乘法求取最佳积分速度的波浪预报,如式(12),所得曲线如图7.此时目标函数式(9)计算的误差平方和仅为271.439 cm2·s-2.

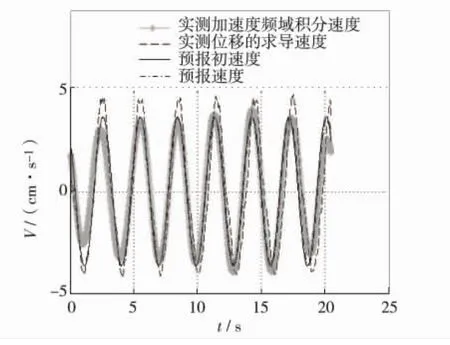
图7 舰船波浪运动预报积分速度Fig.7 Integral velocity of ship wave movement forecasting
由图7可见,波浪预报取得较好效果,但在末端有较大的相位误差,这主要是由于计算目标函数时,舍去末端数据造成的.而且由于积分数据本身的速度幅值较实测位移求导速度小,导致预报后的速度数据幅值也偏小,为此做如下改进:
改进1 为重视末端数据,计算区间由301~1 748扩展为301~2 048,而且对式(9)可改进为误差数据的权重平方和,越靠后的数据越有较大的权重,如式(13).

权重矩阵H设置为
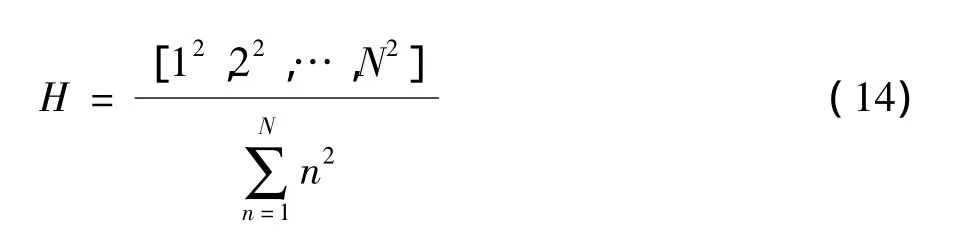
经编程求解得到此时的预报速度函数为
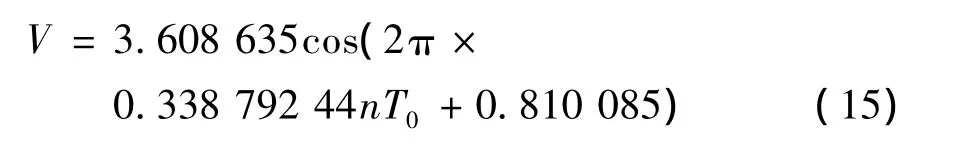
曲线放大如图8,显然末端相位有所改善.

图8 舰船波浪运动改进预报积分速度Fig.8 Improved integral velocity of ship wave movement forecasting
改进2 在改进1的基础上,把预报速度的幅值用相邻积分速度中波高减去波谷的最大值的一半代替.经编程求得峰谷的最大值为4.027 18.

由此得到改进后的曲线如图9.可见,通过频谱波浪预报技术极大修正积分速度的误差,达到较好的积分效果.
2.3 加速度积分速度频谱预报的检验

图9 舰船波浪运动再次改进的预报积分速度Fig.9 Further improved integral velocity of ship wave movement forecasting
以上进行加速度积分为速度和进行频谱预报采用了实测加速度数据中的第1~2 048个数据,为检验加速度积分速度频谱预报在预报上的准确性,对实测加速度数据的第697~2 744个数据进行频域积分处理,对相应数据点的实测位移数据进行求导,并画出速度预报曲线进行比较,如图10.图中改进预报速度2曲线13.51 s之后的数据即为预报的数据.可见,改进后的积分预报速度在图中的7 s内很好地预测了积分速度,但与积分速度一样,与实测位移的求导速度有很小的相位误差,这主要是由于数据采样时,有少数数据的采样时间多于10 ms,而在频域积分时一律按10 ms处理造成的.

图10 舰船波浪运动预报积分速度的预报检验Fig.10 Test of forecasting integral velocity of ship wave movement
3 舰船波浪运动加速度积分位移频谱预报处理
3.1 加速度积分速度频谱预报初步处理
采用同样的预报方法对频域积分位移进行处理,其功率谱如图11.在第8个数据点处有最大功率1.228 24×103cm2/s3,此时频率为 0.341 769 Hz,相位为-0.781 484 rad.在第301~1 748个数据点范围内的积分位移幅值的均值为1.782 8 cm.

图11 频域积分位移的功率谱Fig.11 Power spectrum of integral displacement in frequency domain
因此,可设计算采用的初始预报位移为


图12 舰船波浪运动积分预报初始位移Fig.12 Original displacement velocity of ship wave movement forecasting
3.2 加速度积分位移频谱预报
利用改进的方法1,以式(13)为目标函数利用最小二乘法在第301~2 048个数据点范围内求得的预报位移函数为

改进后预报函数的曲线末端放大图如图13.可见,末端相位得到改善,但幅值偏小,为此再应用改进方法2作出改进函数如式(19),最终预报曲线如图14.可见,舰船波浪运动最终的预报积分位移曲线很好地修正了积分位移的误差,与实测位移曲线非常逼近.


图13 舰船波浪运动改进预报积分位移Fig.13 Improved integral displacement of ship wave movement forecasting
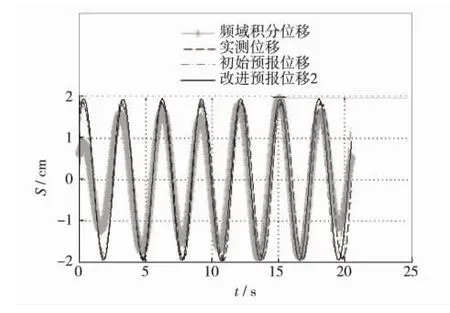
图14 舰船波浪运动再次改进的预报积分位移Fig.14 Further improved integral displacement of ship wave movement forecasting
3.3 加速度积分位移频谱预报的检验
以上进行位移积分和频谱预报采用实测加速度数据中的第1~2 048个数据,为检验加速度积分位移频谱预报在预报上的准确性,对实测加速度数据的第697~2 744个数据进行频域积分处理,并画出相应数据点的实测位移曲线进行比较,如图15.图中改进预报位移2曲线13.51 s之后的数据即为预报数据.由图15可见,改进后的积分预报位移在图中的7 s内很好地预测了积分位移.
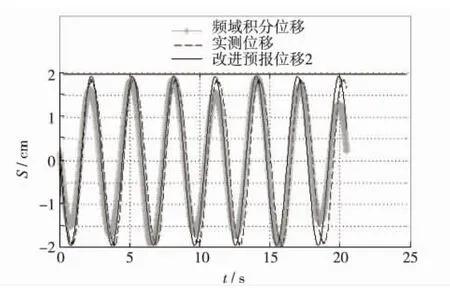
图15 舰船波浪运动预报积分位移的预报检验Fig.15 Test of forecasting integral displacement of ship wave movement
结 语
通过改进频谱波浪预报技术,使之用于舰船波浪运动模拟平台实测加速度频域积分速度和位移的修正,取得良好效果,极大地纠正了积分速度和位移的误差,且可对舰船波浪运动在较长时间内进行有效预报.本研究改进了基于加速度阵列的舰船过驳波浪运动检测系统的积分处理,使之达到更高精度;对舰船过驳波浪运动的成功预报有助于控制系统提前动作,解决执行机构的大惯量滞后问题.
/References:
[1]Chen Aiguo,Ye Jiawei,Chen Yuanming.Measurement principle of ship wave movement based on accelerometer array[J].Journal of Shenzhen University Science and Engineering,2010,27(3):374-378.(in Chinese)陈爱国,叶家玮,陈远明.基于加速度计阵列的舰船波浪运动检测 [J].深圳大学学报理工版,2010,27(3):374-378
[2]Chen Aiguo,Ye Jiawei,Su Shu,et al.Measuring and processing about the acceleration of experimental platform simulating ship wave movement[J].Shipbuilding of China,2011,52(3):83-90.(in Chinese)陈爱国,叶家玮,苏 曙,等.舰船波浪运动模拟平台加速度数据检测与处理 [J].中国造船,2011,52(3):83-90.
[3]Chen Aiguo,Ye Jiawei.Experimental study on acceleration measurement and numerical integral of ships wave movement[C]//The 21st International Offshore and Polar Engineering Conference. Hawaii(USA):ISOPE,2011,148-151.
[4]Chen Aiguo,Ye Jiawei,Chen Yuanming.Measurement Technique and Data Processing of Ship Wave Movement[J/OL].[2012-10-17].Science Paper Online,http://www.paper.edu.cn/index.php/default/releasepaper/content/201210-158.(in Chinese)陈爱国,叶家玮,陈远明.船舶波浪运动检测技术与数据处理 [J/OL].[2012-10-17].中国科技论文在线,http://www.paper.edu.cn/index.php/default/releasepaper/content/201210-158.
[5]Chen Aiguo.Study on the Key Technique of New Wavemovement Compensative System for Sealift Ships[D].Guangzhou:South China University of Technology,2011.(in Chinese)陈爱国.新型舰船过驳波浪补偿系统关健性技术研究[D].广州:华南理工大学,2011.
[6]Chen Yuanming,Ye Jiawei,Wei Dong.Experimental study on a stable platform system having the function of wave motion compensation[J].Machine Tool& Hydraulics,2008,36(4):67-71.(in Chinese)陈远明,叶家玮,魏 栋.波浪运动补偿稳定平台系统的试验研究 [J].机床与液压,2008,36(4):67-71.
[7]Ye Jiawei,Chen Yuanming,Wang Dongjiao,et al.Wave motion compensation scheme and its model tests for the salvage of an ancient sunken boat[J].China Ocean Engineering,2006,20(4):635-643.
[8]Chen Aiguo,Ye Jiawe.Research on four layer back propagation neural network for the computation of ship resistance[C]//Proceedings of IEEE International Conference on MechatronicsandAutomation.Changchun(China):IEEE Press,2009:2537-2541.
[9]Chen Aiguo,Ye Jiawei.Research on the genetic neural network for the computation of ship resistance[C]//Proceedings of International Conference on Computational Intelligence and Natural Computing.Wuhan(China):IEEE Press,2009:366-369.
[10]Schellin T E,Beiersdorf C,Chen X B,et al.Comparative frequency domain sea keeping analysis of a fast mono hull in regular head waves[C]//Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering.Oslo(Norway):ASME,2002:753-760.
[11]Storhaug G.Experimental Investigation of Wave Induced Vibrations and Their Effect on the Fatigue Loading of Ships[D].Oslo(Norway):Norwegian University of Science and Technology,2007.
[12]Magnusson A K,Reistad M.Guide to Wave Analysis and Forecasting[M].Geneva(Switzerland):Secretariat of the World Meteorological Organization,1998:34-42.
[13]Reistad M,Magnusson A K.Guide to Wave Analysis and Forecasting[M].Geneva(Switzerland):Secretariat of the World Meteorological Organization,1998:57-66.
[14]Kim K,Jurnalov C D,Ham S.Mechanisms of female urinary continence under stress:frequency spectrum analysis[J].Journal of Biomechanics,2001,34(5):687-691.
[15]Wilson R V,Carrica P M,Stern F.Unsteady RANS method for ship motions with application to roll for a surface combatant[J].Computers and Fluids,2006,35(5):501-524.
[16]Zhang Y,Ong W,Arakelyan I,et al.Polaron-to-polaron transitions in the radio-frequency spectrum of a quasi-twodimensional Fermi gas [J].Physical Review Letters,2012,108(23):235302-235307
[17]Jeong Chayjeon,Jae Hyunkim,Jae Geunyoo,et al.Frequency spectrum analysis of corona discharge source measured by ultrasound detector[C]//International Conferences on Computer Applications for Modeling,Simulation and Automobile.Jeju Island(Korea):Springer-Verlag Press,2012:294-299.
[18]Nakajima T,Shingyoji M,Anayama T,et al.Spectrum analysis of endobronchial ultrasound for prediction of lymph node metastasis in patients with lung cancer[J].Chest Journal,2012,142(4):1251-1258.
[19]Liu Can,Wu Jingquan,Li Guanghui,et al.Frequencyspectrum characteristics of force in end milling with tool wear and eccentricity[J].The International Journal of Advanced Manufacturing Technology,2012,23(3):10-24.
[20]Dai Chunyang,Zhang Xiaoling.A novel two-dimensional frequency spectrum for bistatic SAR processing[C]//IEEE CIE International Conference on Radar.Chengdu(China):IEEE Press,2011:1551-1553.
