参量放大脉冲发生器中泵浦波相位调制的研究

王 哲，李齐良，丰 昀

(杭州电子科技大学通信工程学院，浙江杭州310018)

0 引言

参量放大是一种基于四波混频(Four-Wave Mixing，FWM)的非线性过程。在光网络中，参量放大器(Fiber Optical Parametric Amplifier，FOPA)在超快全光处理过程中有很多的应用［1－3］，其中一种重要的应用是作为光通信系统中的波长转换器［4］。通过将泵浦波和信号波一同输入到放大器中，可以在所希望的波长上产生闲频波，由于这个过程中产生的闲频波将与信号波以相同的脉冲序列出现，所以通常是利用FWM将信号波脉冲数据转移到产生的闲频波上［5］。当需要在某个波长上得到脉冲序列时，通过调制泵浦波功率也能做到［6］。通常由于泵浦波功率较大，需要先进行相位调制来抑制布里渊散射(Stimulated Brillouin Scattering，SBS)［7］。本文分析了泵浦波的相位调制如何对闲频波脉冲产生影响的。

1 脉冲产生理论

单泵浦结构的FOPA是基于简并的四波混频过程的，通过将频率为ωp的泵浦波和频率为ωs的信号波一同输入到高非线性光纤，满足一定相位条件时可以产生频率为ωi=2ωp－ωs的闲频波。考虑泵浦波功率远大于信号波的情况下，泵浦波、信号波与产生的闲频波在光纤的演化可以用下面3个耦合方程描述［8］:

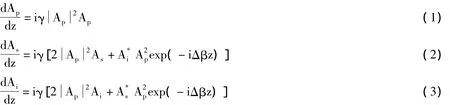
式中，p=|Ap|2为泵浦波的功率，线性相位失配量 Δβ=β2Δ+β4/12Δ，其中 Δωs=ωs－ωp。β2和β4为泵浦波频率ωp处的色散系数。

采用长度为100m、γ=0.015W－1/m的高非线性光纤。输入脉冲的峰值功率为2W，工作波长为1550.5nm;在零色散波长为1550nm附近，二阶色散系数β2=－2.9×10－28s2/m，三阶色散系数β3=1.2 ×10－4ps3/m，四阶色散系数 β4= －8.4 ×10－55s4/m。

由于最初输入端仅泵浦波和信号波的输入，而没有闲频波，所以用Ps(z)/Ps(0)表示闲频波的增益:

式中，P为泵浦波功率，g为参量增益。

在不同信号波频率下，泵浦波功率变化引起参量增益变化的快慢是不同的。为了产生较短脉宽的闲频波脉冲，必须寻找一个最佳的信号波频率，引入增益敏感度［9］:

泵浦波功率变化对参量增益的影响如图1所示，增益敏感度随失谐量Δβ/(γP)的变化曲线如图2所示。

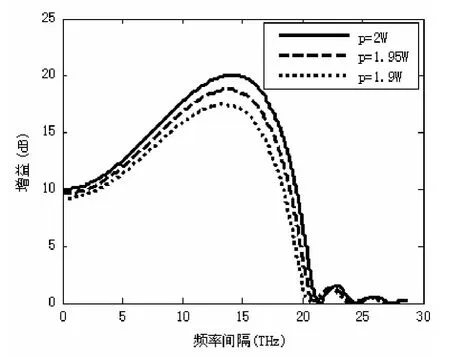
图1 不同泵浦波功率下的增益曲线

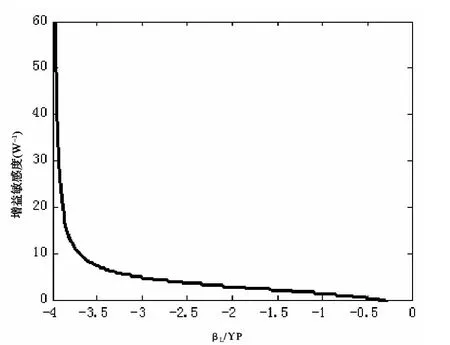
图2 增益敏感度随失谐量βL/γP变化的曲线

图1中，泵浦波功率的变化会引起参量增益谱的变化。随着泵浦波功率从2W减小到1.9W，增益的幅度和范围有一定程度的减小，原来处于增益谱边缘频率的信号波就有可能落在增益范围之外，对应生成的闲频波也是如此。所以当输入的泵浦波功率下降时，参量增益突然减小甚至消失。这样，在闲频波的频率处就可以产生脉冲了。

图2中的横坐标的含义为Δβ/(γP)，表示相位匹配的失谐量。它表明，当Δβ接近－4γP时，放大器将获得较大的增益敏感度，此时获得的脉冲将具有比较小的脉宽。

2 相位调制

当泵浦波功率较大时，容易发生布里渊散射，所以需要在泵浦脉冲输入FOPA之前对其进行相位调制［10］。为了了解泵浦波相位调制对产生的闲频波脉冲的影响，引用文献11中的调制不稳定性模型，忽略光纤损耗的影响并包含二阶至四阶的色散项在内，非线性薛定谔方程可以写为:

式中，A(z，)为慢变场幅度，为以泵浦波群速度移动的时间量，βm为色散系数。

对连续泵浦波稳态解加入微扰μ(z，)和相位因子φ()，得到:

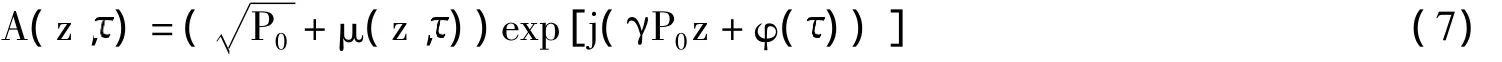
通过对μ(z，)进行线性化并只保留相位的一阶导数∂φ/∂，得到:

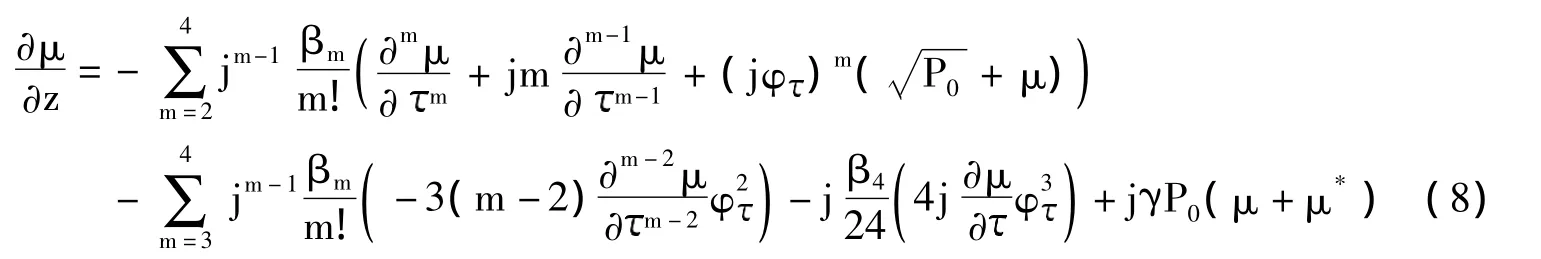
假设小信号的一般解为:

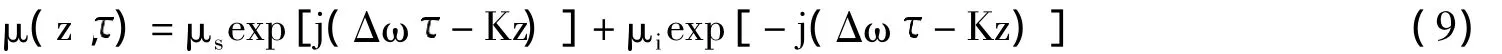
式中，μs和μi分别代表信号波和闲频波的幅度，Δω=ωp－ωs为信号波与泵浦波之间的频移量，K为波数。将式9代入式8中求解得出参量增益［11］:

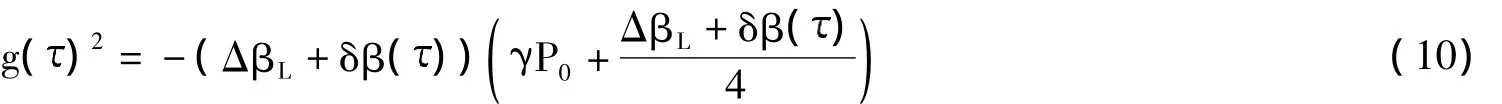
式中，泵浦波相位调制引起的瞬时相位匹配δβ()=β2φ2－β3［φ Δω2+1/(3φ3)］+β4/12(φ4+6φ2Δω2)。从式10中，可以看出泵浦波相位调制使得相位匹配项变得与时间有关。如果δβ()=0，也就是泵浦波无相位调制的情况，参量增益就回到了一般情况。相位调制对增益谱的影响如图3所示。

从图3中可以看到，在相位变化的下降沿阶段时，增益谱的边缘处向右扩张了;而在相位变化的上升沿，增益谱向左边收缩。

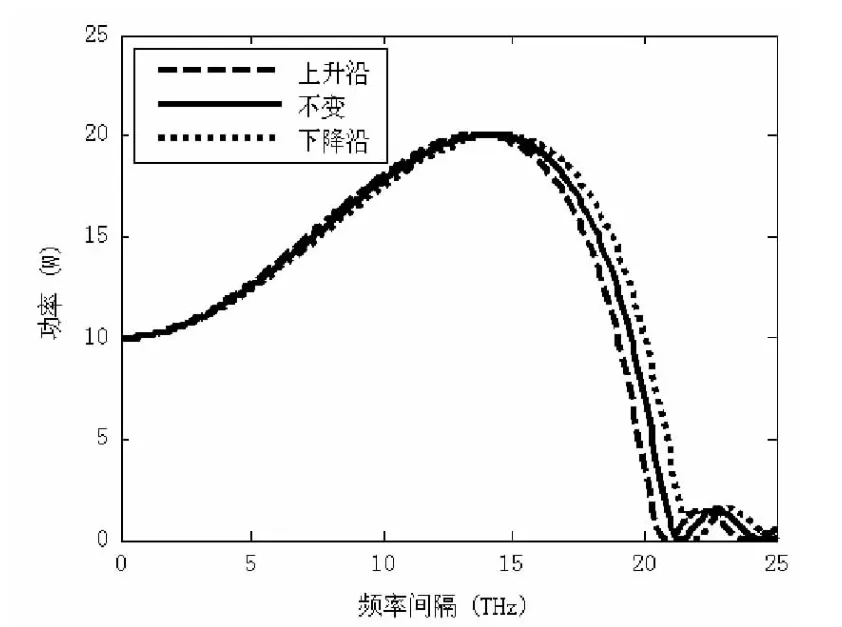
图3 泵浦波相位调制时增益谱的变化情况

仿真时，假设为无初始啁啾的双曲正割脉冲的幅度形式Ap=sech(T/T0)，脉冲的重复率为20GHz。泵浦波的相位调制方式是被频率为3GHz的伪随机序列调制的二进制相移键控，且序列的边沿上下时间为20ps，上升沿、下降沿引起的瞬时频移分别取0.025THz和－0.025THz。在泵浦波相位调制的情况下，得到的闲频波脉冲如图4所示。

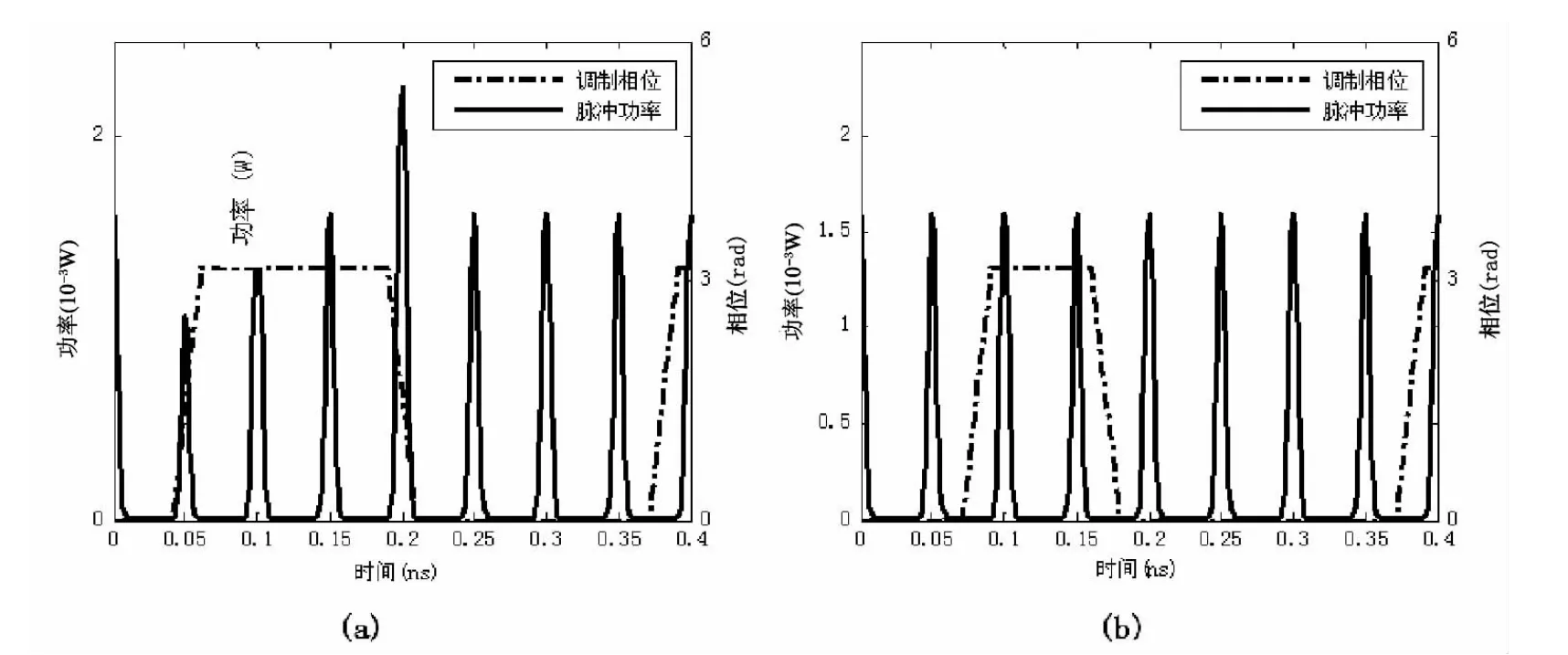
图4 相位调制对闲频波脉冲序列的影响

图4(a)中，泵浦波相位的变化使得脉冲功率不整齐。在相位上升沿持续时间段内，脉冲峰值功率下降，下降沿时间段内，峰值功率增大。这是因为，为了获得脉宽较小的脉冲，仿真中信号波与泵浦波频率间隔保持在19.3THz，也就是增益谱的边缘处，而功率一定时，泵浦波相位调制对边缘增益谱的影响是:上升沿时，增益减小;下降沿时，增益增大。

为了避免相位调制引起的这种起伏变化，调整图4(a)中泵浦的相位调制情况，使得PRBS序列的比特率为5Gbit/s，并且初相位在无脉冲产生的时间段内发生跳变，调整后的闲频波脉冲如图4(b)，从图4(b)中可以看出，当泵浦波相位上升、下降沿总是处于脉冲之间的间隙时，可以产生峰值功率非常整齐的脉冲序列。

3 结束语

本文分析了基于参量放大器的脉冲产生原理。通过输入泵浦波脉冲，可以在目标波长上获得闲频波脉冲。为了减小布里渊效应的影响，需要对泵浦波脉冲进行相位调制，这将导致闲频波脉冲峰值功率出现起伏。通过调整泵浦波的调制频率及其初始相位，使得泵浦波相位的跳变仅发生在相邻脉冲的间隙内，可以获得峰值功率比较平稳的脉冲序列。

［1］ Hansryd J，Andrekson PA，Westlund M，et al.Fiber-based optical parametric amplifiers and their applications［J］.IEEE Journal of Selected topics in quantum electronic，2002，8(3):506 －520.

［2］ Wong C S，Tsang H K.Polarization-independent time-division de multiplexing using orthogonal-pumps four-wave mixing［J］.IEEE Photonic Technology Letters，2003，15(1):129 －131.

［3］ Kuo B PP，Wiberg A O J，BrèC S，et al.Ultrafast clock recovery and sampling by single parametric device［J］.IEEE Photonics Technology Letters，2011，23(3):191 －193.

［4］ Marhic ME，Park T.Broadband fiber-optical parametric amplifiers and wavelength converters with low-ripple Chebyshev gain spectra［J］.IEEE Optics Letters，1996，21(17):1 354 －1 356.

［5］ Tanemura T，Goh C S，Kikuchi K，et al.Highly efficient arbitrary wavelength conversion within entire C-band based on nondegenerate fiber four-wave mixing［J］.IEEE Photonics Technology Letters，2004，16(2):551 －553.

［6］ Zhou Y，Kuo B PP，Cheung K K Y，et al.Wide-band generation of picoseconds pulse using fiber optical parametric amplifier and oscillator［J］.IEEE Journal of Quantum Electronics，2009，45(11):1 350－1 356.

［7］ Yeniay A，Delavaux JM，Toulouse J，et al.Spontaneous and stimulated brillouin scattering gain spectra in optical fibers［J］.Journal of Light wave Technology，2002，20(8):1 425 －1 432.

［8］ Cappellini G，Trillo S.Third order three-wave mixing in single－mode fibers:Exactsolutions and spatial instability effects［J］.Optical Physics，1991，8(4):824 －838.

［9］ Vedadi A，Ariaei A M，Jadidi M M，et al.Theoretical study of high repetition rate short pulse generation with fiber optical parametric amplification［J］.Journal of Light wave Technology，2012，30(9):1 263 －1 268.

［10］ Yaman F，Radic S，Agrawal G P，et al.Impact of pump-phase modulation on dual-pump fiber-optic parametric amplifiers and wavelength converters［J］.IEEE Photonics Technology Letters，2005，17(10):2 053 －2 055.

［11］ Mussot A，Durécu-Legrand A，Lantz E，et al.Impact of Pump Phase Modulation on the Gain of Fiber Optical Parametric Amplifier［J］.IEEE Photonics Technology Letters，2004，16(5):1 289－1 291.