基于鱼群算法的仿人机器人步态优化

卢嘉敏，杨宜民，付根平

(广东工业大学自动化学院，广东广州510090)

双足步行是仿人机器人实现其他功能的前提和基础，是仿人机器人基本的特征和研究的热点.因为仿人机器人具有结构复杂、高阶数、非线性、强耦合等特点，故采用传统方法难以对其进行良好的控制，所以必须对步态进行优化.文献[1]假设步态的切换是瞬时进行的，用被动冲击方程对切换过程进行建模，实现了五连杆无足平面双足机器人的能量最优、力矩最优的步行和跑步步态.文献[2]不考虑侧向运动的影响，通过一种力矩最优的步态优化方法得到能量最优的步态.而文献[3]在文献[2]的基础上通过增加稳定性约束，得到了能耗最小的优化步态，但仍在二维平面内研究机器人的步态，不适合仿人机器人在三维空间的步态优化.文献[4]以关节力矩变化最小为目标，优化出稳定的步态，但该方法过程较复杂，只是得到了力矩最小而不是ZMP稳定裕度最大的步态.

1 步态规划及其稳定性分析

1.1 基于样条插值的步态规划

仿人机器人步态可以分为起步、周期步行和止步3个阶段.3个阶段都要满足无奇异位姿、ZMP稳定性约束、运动协调性和关节角度范围限制等约束条件[5-9]，故在起步阶段需先让仿人机器人的膝关节弯曲再执行起步，起步完成后进入周期步行阶段，在进入止步阶段后需在双足合拢时把双膝伸直，恢复仿人机器人起步前的直立状态，以此完成止步.在径向和侧向平面内把仿人机器人简化成图1所示的连杆模型，采用三次样条插值方法[10]规划出步态中的肩关节、踝关节和髋关节的运动轨迹，即θarm=f(θa，t)，xankle=f(xa，za，t)，xhip=f(dxs，dxe，t)和yhip=f(dys，dym，dye，t)(其中 θarm为手臂的肩关节摆动角，xankle为踝关节的位置，xa和za为各关键时刻踝关节的位置，xhip、yhip为髋关节的径向、侧向位置，dxs、dxe分别为摆动脚落地时和离地时髋关节到支撑腿踝关节的距离，dys、dym、dye分别为摆动脚落地、离地和抬到最高点时髋关节中心在y轴方向上的坐标)，然后利用几何关系由踝关节和髋关节的轨迹计算出膝关节的轨迹，最后通过逆运动学方程求得各关节的角度轨迹.

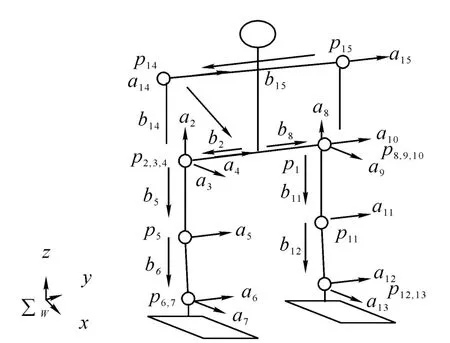
图1 仿人机器人的连杆模型Fig.1 Link model of humanoid robot

1.2 腿部各关节对步态稳定性的影响分析

仿人机器人的步态稳定性由ZMP的稳定裕度决定.ZMP的稳定裕度是指机器人步行的ZMP值离有效稳定区域边缘的最小距离，ZMP的稳定裕度越大，机器人的稳定性能越好，即ZMP点越接近有效稳定区域中间时机器人的步态越稳定.

跟据 ZMP 的计算公式[11]:

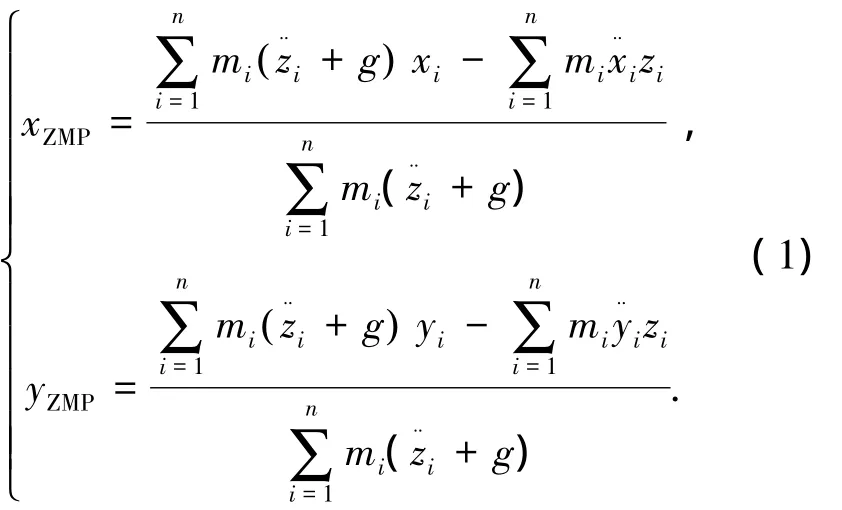
式中:mi为连杆i的质量，xi、yi、zi为连杆i的质心位置，g为重力加速度.由于ZMP的x分量和y分量类似，为了避免重复，下文只分析ZMP的x分量.把各连杆位姿与关节角度的关系代入式(1)后，得到式(2)所示的ZMP的x分量表达式:

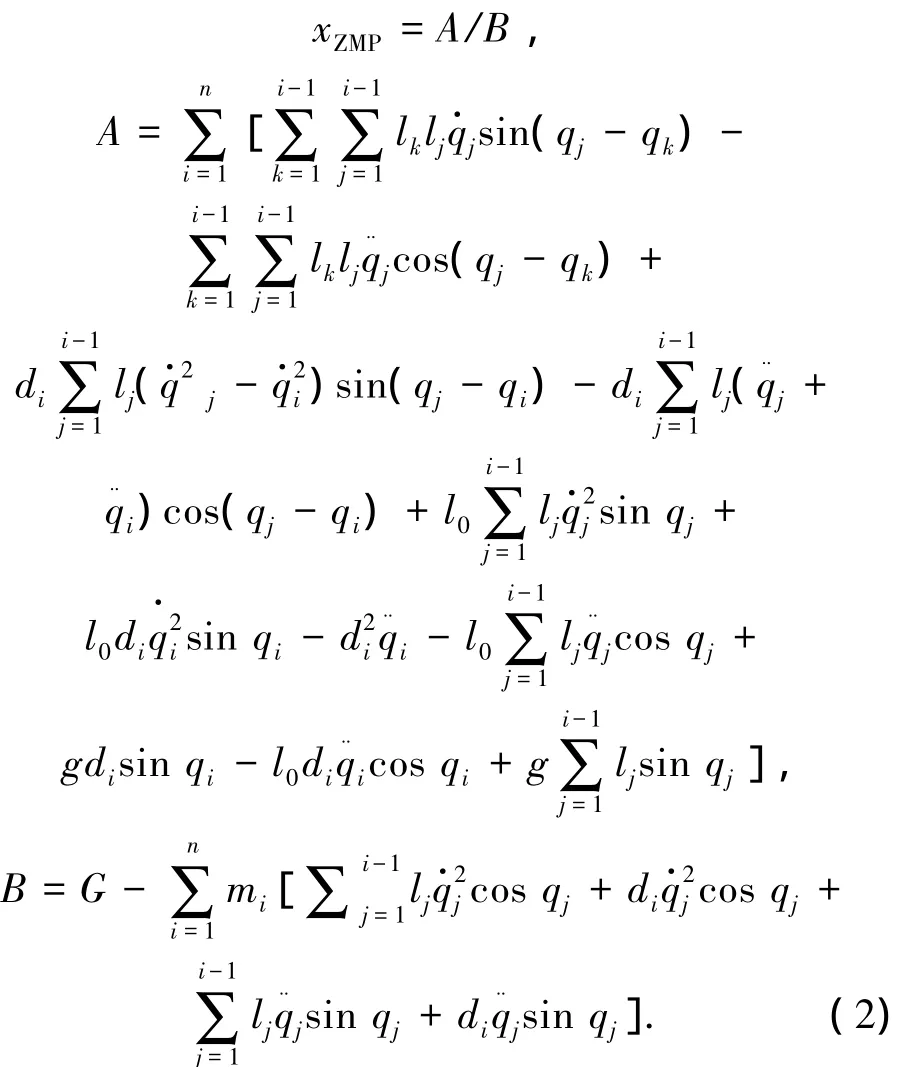
式中:li、di分别为连杆i的长度和连杆质心到相应关节的距离，qi为连杆i与z方向的夹角.

由于仿人机器人的质量主要集中在躯干，而髋关节是控制上半身躯干位姿的主要关节，所以髋关节对ZMP轨迹和机器人的步态稳定性的影响很大.踝关节位姿是规划仿人机器人落脚点、摆动脚高度和调节机器人步速的关键关节，摆动脚高度会影响到机器人的双脚力矩和能耗，步速的快慢会直接影响到ZMP的变化速率，从而影响机器人的稳定性.膝关节是根据踝关节和髋关节轨迹通过几何关系计算出的，故其对步态稳定性的影响没踝关节和髋关节大.图2为根据式(2)计算所得的踝关节、髋关节以及膝关节对仿人机器人步态ZMP的影响图，由图可验证，踝关节和髋关节对ZMP的影响较大，对仿人机器人的ZMP稳定裕度有较大影响，其中踝关节和髋关节在起步步行阶段对仿人机器人步态的稳定性影响最为明显，该影响随着机器人步态进入周期步行阶段和止步步行阶段逐渐减少，而膝关节在步态的起步步行、周期步行和止步步行阶段对仿人机器人步态的稳定性影响都较小，可忽略不计，因此，对髋关节和踝关节进行优化可以获得ZMP稳定裕度更大的仿人机器步态.

图2 髋、踝和膝关节对机器人步态稳定性的影响Fig.2 Influence of hip，ankle and knee joints on robot＇s gait stability

2 基于鱼群算法的步态优化设计

鱼群算法是一种基于模拟鱼群行为来寻找全局优化的群智能算法[12].该算法对比传统的优化模式具有分布处理、寻优速度较快、适应能力强的特点，因此，特别适合用于文中具有多约束条件、多参数的步态寻优.

2.1 鱼群算法

鱼群算法中，人工鱼状态表示为向量 Xi=[xi1xi2…xiD]，i=1，2，…，N(N为人工鱼群个体大小).xiD为第i条人工鱼的第D维向量，每条人工鱼状态就是一个潜在的解，将Xi带入被优化的函数，根据函数值的大小衡量Xi的优劣.人工鱼通过随机解进行初始化，然后通过觅食、聚群及追尾等算子来更新自己，迭代搜寻最优解，从而实现寻优.其中觅食、聚群、追尾算子和行为选择具体如下.

1)觅食算子.

当人工鱼当前状态为Xi，在其感知范围内随机选择一个状态Xi，如果发现Xi对应的函数值Yj(目标函数)更优，则向该方向前进一步;反之，再重新随机选择状态Xi，判断是否满足前进条件.这样反复尝试try_munber次(觅食行为最大尝试次数)后，如果仍不满足前进条件，则随机移动每步步长.

2)聚群算子.

当人工鱼当前状态为 Xi，探索当前邻域内di，j=‖Xi－ Xj‖ ＜ Visual(di，j为人工鱼个体之间的距离，Visual为人工鱼的感知距离)的伙伴数目nf及中心位置如果Yc/nf＞δYi(δ为拥挤度)，则表明伙伴中心有较多的食物并且不太拥挤，Xi应朝伙伴的中心位置方向前进一步;否则执行觅食算子.

3)追尾算子.

当人工鱼当前状态为 Xi，探索当前邻域内di，j＜Visual的伙伴数目 nf，发现伙伴中 Xi是伙伴中最优的(即Xi对应的Yj为领域内最优解)，如果Yc/nf＞δYi，则表明伙伴Xi的状态具有较高的食物浓度并且其周围不太拥挤，则朝伙伴Xi的方向前进一步，否则执行觅食算子.

4)行为选择

根据所要解决的问题性质，对人工鱼当前所处的环境进行评价，从而选择一种行为.如对于求取极大值的问题，最简单的评估方法可以用试探法，就是模拟执行聚群、追尾等行为，然后评价行动后的值，选择其中的最大者来实际执行，默认的行为方式为觅食算子.

2.2 目标函数的构造

仿人机器人要实现长久稳定的步行，首先要求其步态具有较大的稳定裕度和较小的能耗，故本文以ZMP稳定裕度和整体能耗为参数共同构造目标函数.假设ZMP稳定裕度的目标函数为JZ，整体能耗的目标函数为JA，则目标函数J=αJZ－βJA(其中α、β∈[0，1]，是根据两者对仿人机器人步行时的比重而设定，由于在JZ不变的情况下，能量消耗越小J越大，故JA前为减号).

对于JZ，由于仿人机器人步态是由单脚支撑和双脚支撑交替作用实现的，故要对JZ进行分段讨论.在步行的单脚支撑期，ZMP必须在支撑脚内才能保证其步态的稳定性.假设在第i个采样时刻，ZMP到脚内有效稳定区域的x、y方向边界的最小距离分别为dx、dy:

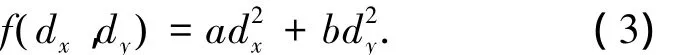
式中:a+b=1，且 a/b=Lfoot/Wfoot(Lfoot、Wfoot分别为机器人脚掌的长和宽)，则单脚支撑期内ZMP的目标值函数为

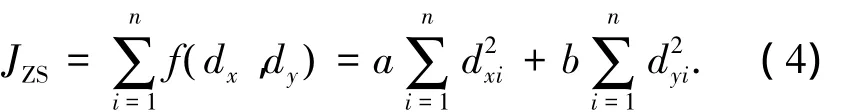
在双脚支撑期，ZMP的稳定区域为双脚足底所构成的六边形，如图3所示.

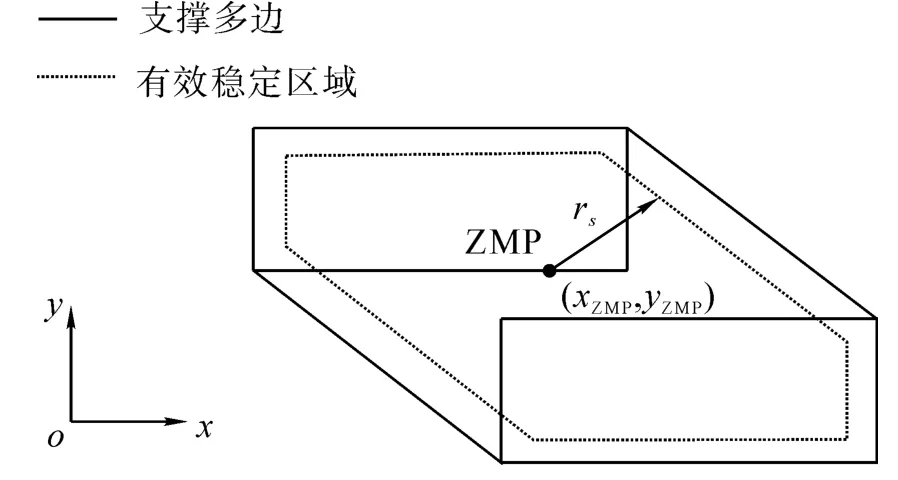
图3 双足支撑期稳定区域Fig.3 The diagram of stability region for double phase

设在第j个采样时刻ZMP点到区域边界的最小距离为ds，则双脚支撑期内ZMP的目标值函数为

而在能耗方面，为保证目标函数值的光滑性，考虑到仿人机器人的能耗主要来源于驱动力的损耗，所以采用驱动力矩的函数来描述JA，即

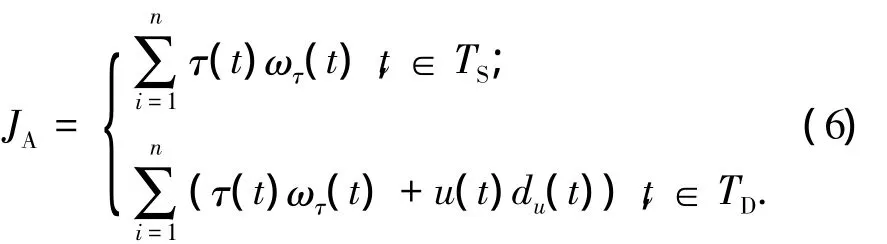
式中:τ为关节驱动力矩，ωτ为关节角速度，u为双脚支撑期双脚受到的总力矩，du为双脚支撑期双脚受到的总力矩作用于机器人的力臂长，TS为单脚支撑期，TD为双脚支撑期.终上所述，用于优化的最终总目标函数为

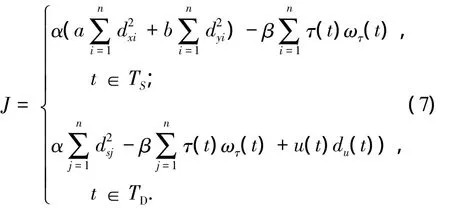
2.3 基于鱼群算法的步态优化流程

1)初始化各参数值，设定人工鱼群规模N、步长Step、拥挤度δ、最多尝试数try_munber、delta、最大迭代次数maxgen，并设置迭代次数gen=1;

2)在待优化步态参数的取值范围内初始化鱼群，随机得到 X1，X2，…，XN{}，并由其计算出鱼群中各鱼之间的平均距离作为感知距离Visual，根据式(7)计算出各人工鱼的食物浓度J，取最大者Jmax，并保存其状态;

3)各人工鱼分别执行追尾、聚群和觅食算子，并分别评价对应的J值，取聚群和追尾算子中的最优J值与Jmax比较，如果J优于Jmax状态，便取代之;

4)判断结束条件:根据迭代次数maxgen是否满足条件，若满足条件则结束迭代，输出最优解，否则gen自增1，并转3)继续.

3 仿真实验及结果分析

本文在MATLAB 7.1环境下，以直立状态的仿人机器人弯膝起步，接着周期步行直至停止步行并恢复身体直立状态的步态仿真，以验证本文利用鱼群算法对步态参数优化结果的有效性，同时将基于鱼群算法的仿人机器人步态优化(FSASP)与基于遗传算法的仿人机器人步态优化(GASP)的寻优结果进行比较，说明本文方法的优越性.仿人机器人的结构参数如表1所示.

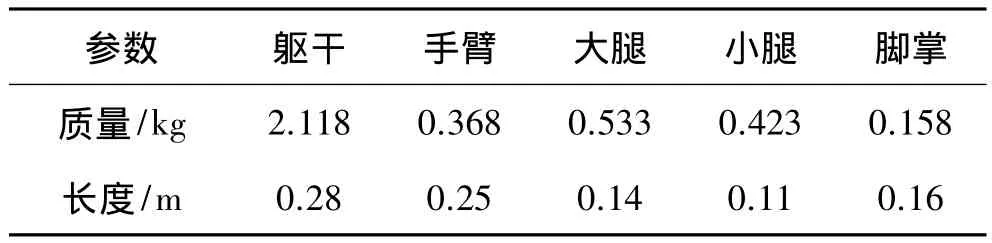
表1 仿人机器人各部分参数Table 1 Configuration parameters of humanoid robot

步态规划方法如前文所述，相应参数为:仿人机器人双臂距离0.20 m，两髋关节距离0.10 m，脚掌宽度0.08 m，脚掌高度 0.045 m，下蹲高度0.03 m，抬脚高度 0.01 m，步长 0.10 m，步行周期 1.2 s，其中单脚支撑期为 0.96 s，双脚支撑期为 0.24 s，采样周期为0.01 s.鱼群算法的相关参数为:N=4，Step=1，Visual=2，try_munber=50，delta=2，maxgen=100，α =0.8，β =0.2.由于鱼群算法采用随机方式初始化鱼群，在重复运行30次鱼群算法，求得的参数平均值如下:dxs=0.041 m ，dxe=0.33 m ，dys=0.039 m ，dym=0.031 m ，dye=0.009 m，把本文优化后的参数值代入步态得到的ZMP轨迹如图4所示，三维步态棍状图如图5所示，稳定裕度结果如图6所示，能耗结果如图7所示.

图4 步态优化后的ZMP轨迹Fig.4 The ZMP trajectory after gait optimization

图5 三维步态棍状图Fig.5 The stick figure of 3-D gait

4 结束语

本文分析了腿部各关节对仿人机器人步态稳定性的影响，在径向和侧向平面内选择对机器人步态稳定性影响较大的关节位置为寻优参数，以步态的ZMP稳定裕度最大和整体能耗最小为目标构造目标函数，采用鱼群算法对基于样条插值方法规划的仿人机器人步态进行优化.仿真结果表明，该方法优化后的步态ZMP稳定裕度大、能耗小、平稳流畅，同时较利用遗传算法对步态进行优化具有更好的全局搜索能力和更快的寻优速度.

图6 步态的ZMP稳定裕度Fig.6 ZMP Stability margin of gait

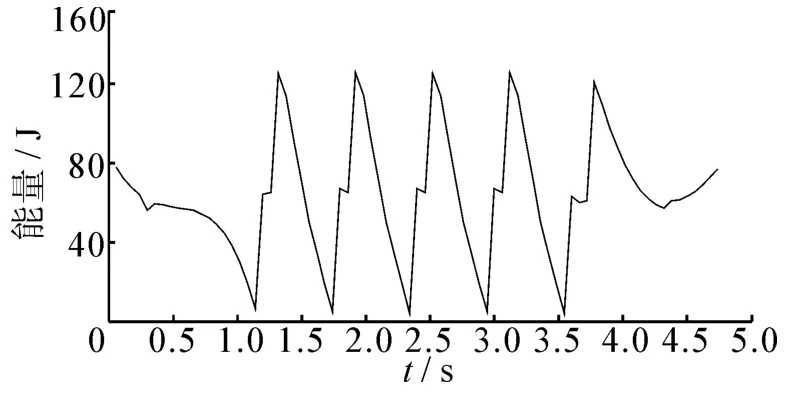
图7 步态的能耗Fig.7 Energy consumption of gait

从图4～7可以看出，起步、周期步行和止步3种步态的ZMP轨迹基本位于支撑区域中心，ZMP的稳定裕度大，步行的功率最小值和最大值分别为4.079 J、125.4 J，平均能耗为 76.2 J，仿人机器人步行自然、流畅、平稳、能耗低，验证了优化结果的有效性.

表2为将FSASP和GASP分别重复运行30次，得到的寻优结果.由表2可知，在对仿人机器人步态优化中，本文FSASP相对于GASP更能脱离局部最优收敛到全局最优，而且本文FSASP在30次的寻优仿真中，寻优平均耗时为6.97 s，而GASP寻优平均耗时为15.40 s，即本文FSASP相对于GASP寻优速度更快.

表2 2种方法30次重复优化的结果Table 2 30 repeated optimization results of the two methods

[1]CHEVALLEREAU C，AOUSTIN Y.Optimal reference trajectories for walking and running of a biped robot[J].Robotica，2001，19(5):557-569.

[2]BESSONNET G，SEGUIN P，SARDAIN P.A parametric optimization approach to walking pattern synthesis[J].The International Journal of Robotics Research，2005，24(7):523-536.

[3]SHI Z，XU W，ZHONG Y，et al.Optimal sagittal gait with ZMP stabillity during complete walking cycle for humanoid robots[J].Journal of Control Theory and Applications，2007，5(2):133-138.

[4]NGUYEN T P，DAE W K，HAK K K，et al.An optimal control method for biped robot with stable walking gait[C]//2008 2th IEEE-RAS International Conference on Humanoid Robots.Daejeon，USA，2008:211-218.

[5]SHAFII N，KHORSANDIAN A，ABDOLMALEKI A，et al.An optimized gait generator based on Fourier series towards fast and robust biped locomotion involving arms swing[C]//IEEE International Conference on Automation and Logistics.Piscataway，NJ，USA:IEEE，2009:2018-2023.

[6]KAYNOV D，SOUERES P，PIERRO P，et al.A practical decoupled stabilizer for joint-position controlled humanoid robot[C]//The 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway，NJ，USA，2009:3392-3397.

[7]伊强，陈恳，刘莉，等.考虑综合行走约束的仿人机器人参数化3D步态规划方法[J].机器人，2009，31(4):342-350.YI Qiang，CHEN Ken，LIU Li，et al.3D parametric gait planning of humanoid robot with consideration of comprehensive biped walking constraint[J].Robot，2009，31(4):342-350.

[8]KIM S，KIM C，YOU B.Stable whole-body motion generation for humanoid robots to imitate human motions[C]//The 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems.Saint Louis，USA，2009:2518-2524.

[9]PETER S，JAROSLAV T，ZLATKO F，et al.Development of cognitive capabilities for robot Nao in center for intelligent technologies in Kosice[C]//2011 2nd International Conference on Cognitive Info-communications.Piscataway，NJ，USA，2011:1-5.

[10]HUANG Qiang，YOKOI K，KAJITA S，et al.Planning walking patterns for a biped robot[J].IEEE Transactions on Robotics and Automation，2001，3(17):280-289.

[11]棍田秀司.仿人机器人[M].北京:清华大学出版社，2007:87-91.

[12]JIANG Mingyan，WANG Yong.Spread spectrum code estimation by artificial fish swarm algorithm[C]//IEEE International Symposium on IntelligentSignalProcessing，2007，2007:1-6.