卫片RPC参数解算浅谈
2013-11-24
(江西省基础测绘院 江西南昌 330001)
1 研究背景
摄影测量与遥感是对非接触传感器系统获取的影像及其数字表达进行记录、量测和解译,从而获得地球及其环境和其他物体可靠信息的一门工艺、科学与技术。随着遥感技术和航天测绘技术的发展,用于获取摄影测量与遥感数据的传感器也不断增加,其类型和成像方式也越来越多。
共线条件方程作为摄影测量与遥感的核心,也即传感器模型的理论基础。通过共线方程建立严格的几何成像模型,需要获取传感器的各种成像参数,如航空影像的内外方位元素、卫星轨道参数、传感器平台的方位参数等。由于传感器模型建立的是地面点与对应像点之间严格的几何关系,具有较高的定位精度,所以一直是摄影测量学的首选。然而,在卫星影像的传感器参数出于技术保密而不被提供的情况下,则需要通用传感器模型。
开放GIS 组织提出了四种适合实时处理遥感影像的通用成像模型,即多项式模型(Polynomial Model)、格网内插模型(Grid Interpolation Model)、有理函数模型(Rational Function Model)和通用实时成像几何模型(Universal Real-time Image Geometry Mode),它们共同特点是的形式简单,计算速度较快。其中,有理函数模型在过去几年的时间里,被美国军方广泛使用,美国的国家影像测绘局(NIMA)还将有理函数模型作为分发影像数据的标准几何模型之一,特别是IKONOS 卫星影像的广泛应用,有力地推动了对有理函数模型的全面研究。不仅拥有较高的拟合精度,随着高分辨率卫星数据的应用范围的扩大,RFM的优点日益凸显,掌握RFM 对于我国高分辨率卫星数据的广泛应用大有裨益。Space Imaging公司称包含有理函数系数的文件为RPC(Rational Polynomial Coefficient,有理多项式系数)文件,本文浅谈一下RPC 参数的解算流程。
2 有理函数模型解算过程
RFM的参数解算严格传感器模型已知和未知的条件下都可实现,但无论何种条件,RPC( Rational Polynomial Coefficients)解算都需要密集均匀的控制格网点数据。它分为与地形有关方案和与地形无关方案两种解算方法。
在传感器模型是已知的的条件下,我们可以采用与地形无关的方案,否则RPC 参数的解算只能严格依靠控制点采用与地形有关的方案。与地形无关的解算方案的基本思想是把影像等分成m 行n 列,得到一系列像点,再把地形起伏范围均匀分成k层,得到(k+1)个等高程的面,然后,利用星载GPS、卫星姿态测定等数据,按严格几何模型计算在不同高程面上像点的平面位置,由此产生了分布均匀物方格网点数据(即虚拟的物方点坐标数据)。最后,利用最小二乘原理解算RPC 参数。这种解算方案能够使有理函数模型高精度拟合传感器模型,进而取而代之完成摄影测量处理。具体结算步骤如下:
⑴划分格网。格网点应均匀分布在像平面空间的整个区域,将整个影像分成m 行n 列,得到(m+1)×(n+1)个均匀分布的影像点。
⑵高程分层。将整个覆盖区域的高程起伏范围高程k层(一般k>3),每层具有相同的高程Z,得到(k+1)等高程面。
⑶三维格网点的解算利用已知的严格几何模型,计算各像方格网点在每层等高程面上对应的“地面点”的平面坐标X、Y,从而得到m+1)×(n+1)×(k+1)个虚拟物方格网点的三维坐标。从而生成的三维虚拟物方格网点(如图1所示)用于解算RPC 参数,这些三维虚拟物方格网点数量大,且在平面和高程上分布均匀,能够达到很高的拟合精度。
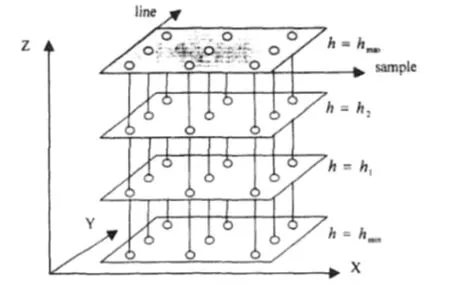
图1 虚拟控制点格网示意图
⑷RPC 参数解算。用以上格网点做控制点,利用最小二乘平差方法解算RPC 参数。
⑸精度检查。采用新的格网划分方式重新生成一定数量均匀分布的地面格网点,用解算出来RPC参数计算这些地面格网点的像方坐标,通过比较RPC 参数的解算结果和检查点就可以确定解算精度。
如果具有至少两幅重叠影像构成立体像对,则可以基于立体影像进行RPC 参数解算。基于立体像对解算RPC 参数时,可以直接使用辅助测量数据或平差后的外方位元素直接进行前方交会,或自动生成DEM,进而获得均匀控制格网点数据。在立体像对中,均匀地量测N个同名像点坐标,然后便可计算出模型点的空间坐标,从而生成控制格网点数据。解算RPC 参数的流程图如图2所示。
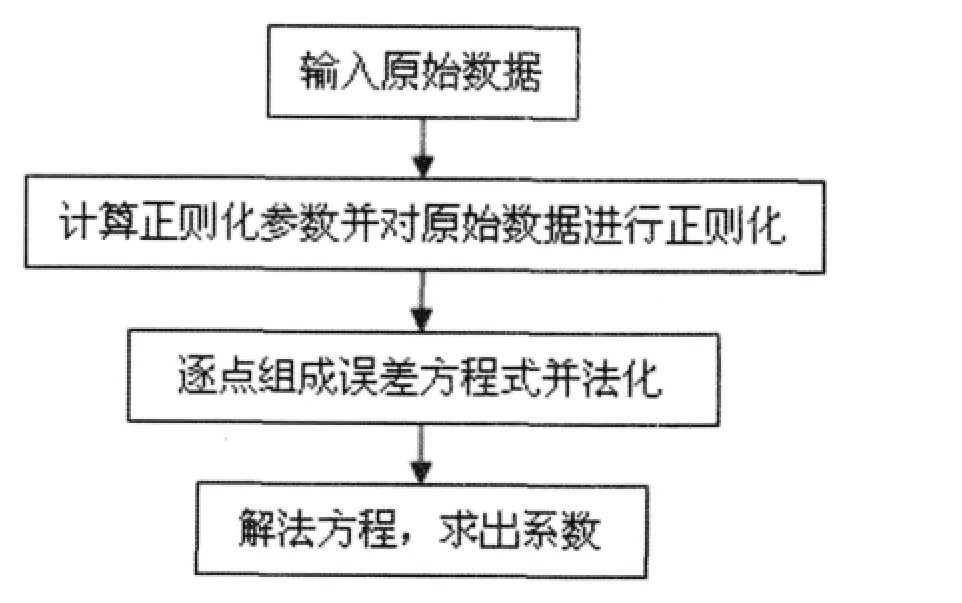
图2 RPC 参数解算流程
[1]王海侠,高飞,胡小华.基于RPC模型的QuickBird 影像几何精校正的研究与探讨[J].城市勘测,2011(3).
[2]李立钢,彭海良,尤红建,周强,许光銮,吴一戎.基于卫星参数预测的高分辨率光学影像精确定位方法[J].测试技术学报,2006,20(4):335-339.
[3]刘军,张永生,王冬红.基于RPC模型的高分辨率卫星影像精确定位.测绘学报,2006(1).
