信息共享对供应链影响的经济学模型分析
2013-11-23田志勇霍灵瑜北京物资学院信息学院北京101149
■ 田志勇 陈 蕾 霍灵瑜(北京物资学院信息学院 北京 101149)
信息共享是供应链中非常重要的研究领域之一。该领域的研究主要集中在信息共享的重要性、激励机制和技术实现三个方面,激励机制或更普遍的机理研究大多是基于供应链信息共享的定量研究,通过建立数理模型进行推导和求解,分析不同情形下信息共享的机制。这方面研究已经取得非常丰富的成果,比如信息共享的最优范围,生产不经济的竞争供应链需求信息共享,横向竞争情形下供应链信息共享等。这些研究基于不同研究理论,比如有的利用基本数理模型理论、利用博弈论和委托代理理论等,有的利用确定性模型理论、也有考虑不确定性因素加以扩展的。但这些研究的前提假设大多是先将关键因素如反需求或供应函数设定为显式函数,特别地,有很多研究将反需求函数假设为线性函数。这种做法虽有效降低了模型的难度、便于数理推导和求解,但同时也降低了模型的精确性、限制了模型的适用范围。由于任何依赖于对某一特定形式的函数选择而产生的性质(结论)都是没有意义的,至少不能简单地加以推广,在这些成果卓著的研究中,我们难以分辨哪些结论是函数的具体形式起到了特殊的作用,从而极大地影响了研究结论的适用范围。
鉴于此,本文尝试基于隐式函数形式,根据实际经济意义假定函数的一些外在特性,以此为基础进行数理推导和分析,提高研究结论的有效性和适用范围。
模型说明
(一)符号
假设供应链包括一个制造商和一个分销商,研究关注于供应链上信息共享和共享费用,从逻辑上将供应链的诸如成本、价格等基本状态信息分为三种类型:一是信息共享前;二是信息共享后不考虑费用;三是信息共享后考虑费用。此外,还需对供应链节点的生产、需求等用通用函数形式表示。因此,有四种类型的基本符号:
1.信息共享前。c为制造商的成本,w为制造商向分销商的批发价,p为分销商向最终用户的销售价。
2.信息共享后不考虑共享费用。c′为信息共享后不考虑共享费用情况下制造商的成本,且c′ 3.信息共享后考虑共享费用。c″为信息共享后考虑共享费用情况下制造商的成本,且c″>c′,w″为信息共享后考虑共享费用情况下制造商向分销商的批发价,p″为信息共享后考虑共享费用情况下分销商向最终用户的销售价。 4.一般函数形式: D=F(p)表示需求函数,D为需求量。 p=f (D)表示反需求函数,为上式的反函数。 M(w)表示批发价w时制造商的供应量,即生产函数且M ′(w)>0。 F(w)表示批发价w时分销商的需求量,即需求函数且F′(w)<0。 Γ(p)表示零售价p时分销商的供应量,即生产函数且Γ′(p)>0。 Ο(p)表示零售价p时最终用户的需求量,即需求函数且Ο′(p)<0。 其中,F(w)=Γ(p)。 基础模型。设需求函数为D=F(p),D为总需求且F′(p)<0,反需求函数为p=f(D)。其中任第i个厂商的销量为Di,则其利润函数为Πi(p)=(f (D)-Φi(Di))Di,根据一阶条件得到等式: 垄断情形下,垄断厂家将根据自己的利润最优确定需求和价格,公式(1)变为表示边际成本,为简单起见用Ψ(p)表示,并将需求函数代入,该式变为:F(p)+[p-Ψ(p)]·F′(p)=0(2) 完全竞争情形下,任何一个厂商的产量Dk的大小不仅对总产量D=F(p),而且对导数F′(p)都微不足道、可以忽略。根据这一特性,以公式(1)为基础,古诺推导出一个重要的方程式: 其中,Ω′(p)>0,这是本文后面进行公式推导的基础。Ω(p)在函数性质上与生产函数等价,从这个意义上,式(3)就是描述微观经济学供需基本均衡状态的方程。前面M(w)和Γ(p)与Ω(p)意义相同,下面将用与其对应的需求函数构建与方程(3)等价的方程式作为分析的基础。 分析模型。如果处于市场均衡状态的产品成本出现变化,将引起价格和收益发生变化,影响途径是“成本变化引起价格变化,价格变化导致收益变化”。为便于分析,假定需求和供给规律不变,即需求和生产函数不变,仅参数发生变化。 将基于制造商和分销商的需求函数和供应函数以及相应成本代入方程式(2)和(3),导出本文分析的基础方程式。 垄断: 制造商的决策方程为: 分销商的决策方程为: 完全竞争: 直觉上,共享销售信息可以降低制造商的制造成本,有多方面原因,比如制造商获得了更准确的需求信息,可以更好地采用JIT和精益制造模式,能够对人员财务和资源等做出更准确的安排,在提高生产效率的同时也使库存、运输等方面的费用下降。同时共享制造信息也可有效地降低分销商的一些相关费用,比如在库存、运输等方面可以做出更有效的安排,减少不必要的消耗、使费用降低等。 根据前面模型说明,信息共享前制造商的成本为c,分销商的批发价为w,分销商的零售价为p;信息共享后制造商的成本降低u变为c-u,分销商的批发价变为w′,分销商的零售价变为p′。信息共享对供应链价格的影响,表现为w′、p′与w、p的关系;对供应链收益的影响,表现为制造商、分销商的收益及二者收益之和。 1.制造商批发价w的变化。我们立足于制造商从生产和需求两个角度分别构建隐函数M(w)和F(w),因M与生产函数同质,是w的增函数,即M′(w)>0;F与需求函数同质,是w的减函数,即F′(w)<0。且: 在共享信息,制造商的制造成本降低u后,对于生产函数M(w)相当于批发价增加u。所以,共享信息后的等式为: 对公式(9)在w处进行泰勒展开,并忽略二阶及高阶项,再将公式(8)代入消去隐函数,得到(w′-w+u)M′(w)=(w′-w) 由于F′(w)<0,M′(w)>0,所以w′-w+u与w′-w异号。 分两种情况: 若w′>w,则都为正,与两者异号的结论矛盾。所以,该假设不成立。 若w′ 因此,得命题1:制造商的成本降低,会导致制造商的批发价降低,但批发价降低幅度小于成本减低幅度。 2.分销商零售价p的变化。同制造商批发价w的分析类似,构建分销商生产函数和需求函数两个隐函数,其中生产函数的生产成本是批发成本,Ω(p)和K(p),其中Ω′(p)>0,K′(p)<0。 假设信息共享后,由于制造商的批发价w变为w′,且w′ 信息共享后,等式变为: 由等式(10)和(11),得 由于Ω′(p)>0和K′(p)<0,所以分子和分母异号。 分两种情况: 若p′>p,则分子分母都为正,与两者异号的结论矛盾。 若 p′ 因此,得命题2:制造商成本降低,会导致批发商的零售价降低,但零售价降低幅度小于批发价减低幅度。 1.制造商收益。记信息共享前,制造商生产量(在市场出清状态下)等于分销商的需求为D,信息共享后为D′。 由于与D、D′相对应的批发价为w、w′,而w >w′,所以D 信息共享前的收益为(w-c)D,信息共享后的收益为(w′-c+u)D′。 由于u>w-w′,所以w′-c+u>w-c。 所以(w′-c+u)D′>(w-c)D,信息共享后制造商收益增加。 2.分销商收益。信息共享前的收益为(p-w)D,信息共享后的收益为(p′-w′)D′。 由于 p-p′ 所以(p′-w′)D′>(p-w)D,信息共享后分销商收益增加。 3.供应链收益。供应链收益为制造商和分销商收益之和,信息共享前的收益为(w-c)D+(p-w)D=(p-c)D,信息共享后的收益为(w′-c+u)D′+(p′-w′)D′=(p′-c+u)D′,有(p′-c+u)D′>(p-c)D。所以,供应链总体收益也增加。 为了实现供应链信息共享,需要投入一定费用,如建立购置设备建设信息系统、开发接口等,不同的措施所需的费用也不一样。为了便于计算,假设采用制造商处建设信息系统,分销商和用户处开发接口的模式,可以忽略除制造商之外的费用。这样信息共享成本由制造商独自承担,相当于产品生产成本提高。 根据前面模型,不考虑信息共享费用时制造商的成本为c-u,分销商的批发价和零售价分别变为w′和p′。考虑信息共享费用后,制造商的成本增加u′,变为c-u+u′,分销商的批发价和零售价分别变为w″和p″。对供应链收益的影响,表现为制造商、分销商的收益及二者收益之和。综合考虑信息共享收益和费用后,其对供应链价格的影响,表现为w″、p″与w、p之间的关系;对供应链收益的影响,表现为制造商和分销商各自的收益及二者收益之和的变化。 如果u>u′,即信息共享的单位收益大于信息共享的单位费用,则结论与上文未考虑信息共享费用时的变化完全一致,区别仅在量的大小方面,用u-u′代替u。所以对于考虑信息共享费用的情况,我们仅研究在u 1.制造商批发价w的变化。第一,完全竞争。与上文处理方式相同得到式由于 F′(w) < 0,M′(w)>0,且u 由此,得命题3:在信息共享费用大于收益从而提高制造商的成本,会导致制造商的批发价提高,但批发价提高幅度小于成本提高幅度。 第二,垄断。垄断情形下,制造商成本提高u′-u,效果与公式(2)中函数Ψ(w)增加一个常数值u′-u相同。假设由于Ψ(w)提高u′-u变为Ψ(w)+u′-u时,w的值变为w+δ。对该式在w处进行泰勒一阶展开,并忽略u′-u和δ的平方及高次幂项,得方程式 根据我们熟知的极大极小理论,即垄断制造商的收益函数的二阶导数小于零,可知上式等号右式分母值为负值。同时,F′(w)<0。所以,增量δ与u′-u同号。但仅通过上式的表达形式,我们还难以对两者做出数量大小的判断。 2.分销商零售价p的变化。第一,完全竞争。与上文处理方式相同得到式由于K′(p)<0,Ω′(p)>0,且w 由此得命题4:在信息共享费用大于收益的情况下,分销商零售价也随之提高,但提高幅度小于制造商批发价提高幅度,也小于制造商成本提高幅度。 第二,垄断。垄断情形下制造商批发价即零售商成本提高δ,则δ=w″-w,效果与公式(2)中函数Ψ(p)增加一个常数值δ相同。假设由于分销商成本提高δ时,p变为p″,设σ=p″-p。对式(2)在p处进行泰勒一阶展开,并忽略δ和σ的平方及高次幂项,得方程式: 上式等号右式分母值为负。同时,K′(w)<0,所以增量σ与δ同号,但两者数量大小方面还难以做出判断。 1.制造商收益。第一,完全竞争。根据命题3,制造商成本提高的幅度大于其批发价提高的幅度,根据需求函数的性质,很容易推出制造商收益下降。记信息共享前,制造商生产量等于分销商的需求量D,信息共享后为D″。 由于与D、D″对应的批发价为w、w″,而w″>w,所以D″ 信息共享前收益为(w-c)D,信息共享后收益为(w″-c+u-u′)D″。 由于u′-u>w″-w,所以w″-c+u-u′ 所以(w″-c+u-u′)D″<(w-c)D,信息共享后制造商收益减少。 第二,垄断。垄断情形下,制造商成本提高u′-u,批发价提高δ,两者同号但大小不确定。记信息共享前,制造商生产量等于分销商的需求量为D,信息共享后为D″。 ∵w 信息共享前的收益为(w-c)D,信息共享后的收益为(w+δ-c+u-u′)D″。虽然根据w 进一步,记信息共享前后收益之差为(w-c)(D-D″)-[δ -(u′-u)]D″。 在一般函数形式下,如果δ 2.分销商收益。第一,完全竞争。根据命题4,分销商成本提高的幅度大于其零售价提高的幅度,根据需求函数的性质,很容易推出分销商收益会下降。记信息共享前,制造商生产量等于分销商的需求为D,信息共享后为D″。 由于与D、D″相对应的批发价为p、p″,而p″>p,所以D″ 信息共享前的收益为(p-w)D,信息共享后的收益为(p″-w″)D″。 由于w″-w>p″-p,所以p″-w″ 所以(p″-w″)D″<(p-w)D,信息共享后制造商收益减少。 第二,垄断。前面已证明,在垄断情形下分销商成本提高w″-w,零售价提高p″-p,两者同号但大小不确定。记信息共享前分销商生产量等于市场需求量D,信息共享后为D″。 信息共享前收益为(p-w)D,信息共享后收益为(p″-w″)D″。虽然依据p 在一般函数形式下,如果w″-w>p″-p即零售价增幅低于批发价增幅,则p-w>p″-w″,此时制造商的收益增加,这与直觉判断相一致。其他情况则会因为函数的形式的不同,亦即需求规律的不同,收益有时提高、有时降低。 3.供应链收益。供应链收益为制造商和分销商收益之和,在未考虑分销商其他成本且市场出清情况下,供应链的利润为零售价减去制造成本后与市场需求量的乘积,即(p-c)D。 完全竞争。由于前面分析,信息共享后制造商和分销商的收益均下降,所以供应链收益也下降。也可从数学表达式进行推导。 信息共享前供应链收益为(p-c)D,信息共享后供应链收益为(p″-c+u-u′)D″,根据上文完全竞争情况下的推导结果有p″>p和p″-p 垄断。信息共享前收益为(p-c)D,信息共享后收益为(p″-c+u-u′)D″。虽然能够判断信息共享前价格低于信息共享后,即p 本文用隐函数形式对需求函数和供应函数等重要因素进行描述,根据背后的经济意义设定函数的诸如凹凸性等外在特性,利用泰勒级数展开等数学公式进行推理,对具有一个制造商和一个分销商的供应链进行信息共享的定量分析,分别考察了供应链成员的成本、价格和收益的变化以及整条供应链的收益变化情况,由此得到一些通用性结论。 在完全竞争情形下,研究结论在直觉上比较容易理解,与以往研究基本相符,所以论文没有利用显函数进行验证;在垄断情形下则比较复杂,在价格方面仅能得到一些变化方向上的判断,在收益方面仅根据隐函数的凹凸性甚至在变化方向上也难以作出具体判断。其原因可能是在完全竞争市场,企业与外部环境的关系以外部环境的单向影响为主,企业被动成分较大,所以其决策对需求和供应函数的具体信息要求则相对较少;而在垄断市场,企业与外部环境的影响是双向的,垄断企业具有较强的主动性,其在决策时对需求和供应函数的具体信息要求则相对较多。即使如此,比较以往采用显式函数的推论,本文的结论更具普遍性。 此外,研究也显示出仅拘于函数的一般形式和特性等有限信息,还有许多地方无法进一步明确,还需要利用显式函数形式或其他信息等更具体特性的支持,但论文的研究已显示出这种方法的有效性和对一些战略性决策的支持。就该方法本身而言,还需要结合诸如弹性系数、根据实际经济意义设定更多函数特性等方面加强研究,充分挖掘其推理的潜力,使得到的结论能够更具体、更深入、更有针对性。 1.常志平,蒋馥.固定比例分担费用情况下信息共享的最优范围研究[J].管理工程学报,2003,17 2.Albert Y.Ha, Shilu Tong, Hongtao Zhang.Sharing Demand Information in Competing Supply Chains with Production Diseconomies[J].Management Science,2011,57(3) 3.陈忠,艾兴政,赵海霞.供应链信息结构与控制结构绩效研究[J].管理工程学报,2010,24 4.张玉林,陈清华.成本信息保护下的供应链协调研究[J].系统工程学报,2008,23(6) 5.吴燕,田大钢.Bertrand竞争下二级供应链信息共享的价值分析[J].工业工程,2010,13 6.邱若臻,黄小原,葛汝刚.信息共享条件下供应链在线与传统销售渠道协调定价[J].管理工程学报,2009,23 7.常志平,蒋馥.供应链中信息共享的最优程度与制度安排[J].上海交通大学学报,2004,38 8.阿维纳什.K.迪克西特.经济理论中的最优化方法[M].格致出版社,2006 9.奥古斯丹·古诺.财富理论的数学原理的研究[M].商务印书馆,1994(二)模型
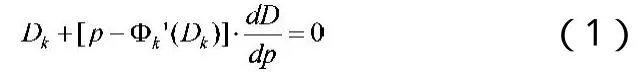

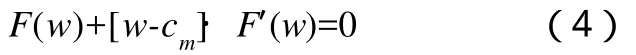
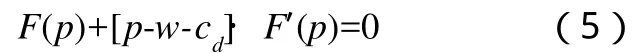

未考虑信息共享费用
(一)批发价、零售价变化分析


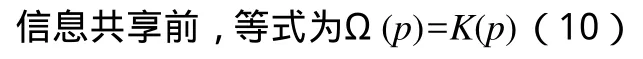

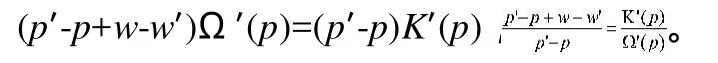
(二)制造商、分销商收益分析
考虑信息共享费用
(一)批发价、零售价变化分析
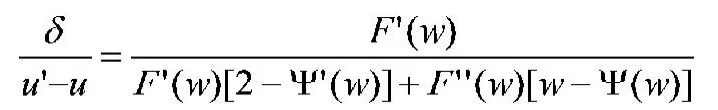
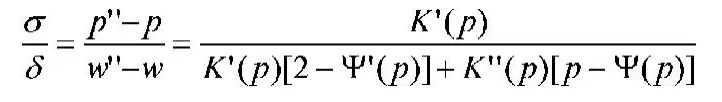
(二)供应链收益分析
结论
